初中数学青岛版九年级上学期 第1章 1.4图形的位似
试卷更新日期:2020-08-12 类型:同步测试
一、单选题
-
1. 下列各选项的两个图形中,不是位似图形的是( )A、
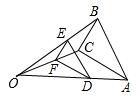 B、
B、 C、
C、 D、
D、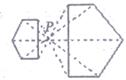 2. 下列说法错误的是( )A、位似图形一定是相似图形 B、相似图形不一定是位似图形 C、位似图形上任意一对对应点到位似中心的距离之比等于位似比 D、位似图形中每组对应点所在的直线必相互平行3. 下列说法中正确的有( )
2. 下列说法错误的是( )A、位似图形一定是相似图形 B、相似图形不一定是位似图形 C、位似图形上任意一对对应点到位似中心的距离之比等于位似比 D、位似图形中每组对应点所在的直线必相互平行3. 下列说法中正确的有( )①位似图形一定是相似图形;
②相似图形一定是位似图形;
③两个全等的位似图形的位似中心在两个图形之间或在这两个图形的公共边上;
④全等图形一定是位似图形,且位似比为1:1;
⑤若图形a与图形b是位似图形,图形b与图形c是位似图形,则图形a与图形c也一定是位似图形.
A、1个 B、2个 C、3个 D、4个4. 在如图所示的网格中,以点O为位似中心,四边形 的位似图形是( )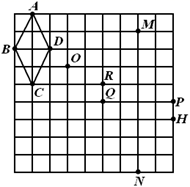 A、四边形 B、四边形 C、四边形 D、四边形5. 将铁丝围成的△ABC铁框平行地面(水平)放置,并在灯泡的垂直照射下,在地面上的影子是△A′B′C′,那么△ABC与△A′B′C′之间是属于( )A、对称变换 B、平移变换 C、位似变换 D、旋转变换6. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 ,那么点B′的坐标是( )
A、四边形 B、四边形 C、四边形 D、四边形5. 将铁丝围成的△ABC铁框平行地面(水平)放置,并在灯泡的垂直照射下,在地面上的影子是△A′B′C′,那么△ABC与△A′B′C′之间是属于( )A、对称变换 B、平移变换 C、位似变换 D、旋转变换6. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的 ,那么点B′的坐标是( )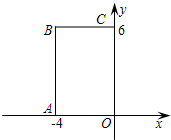 A、(-2,3) B、(2,-3) C、(3,-2)或(-2,3) D、(-2,3)或(2,-3)7. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( )
A、(-2,3) B、(2,-3) C、(3,-2)或(-2,3) D、(-2,3)或(2,-3)7. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( ) A、 B、 C、 D、8. 如图,若△ABC与△A1B1C1是位似图形,则位似中心的坐标是( )
A、 B、 C、 D、8. 如图,若△ABC与△A1B1C1是位似图形,则位似中心的坐标是( )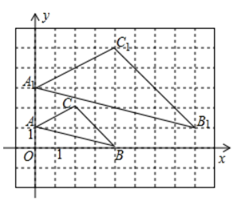 A、 B、 C、 D、9. 如图,△ABC中AB两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C′,且△A′B′C′与△ABC的位似比为2:1.设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A、 B、 C、 D、9. 如图,△ABC中AB两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C′,且△A′B′C′与△ABC的位似比为2:1.设点B的对应点B′的横坐标是a,则点B的横坐标是( )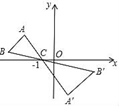 A、 B、 C、 D、10. 按如下方法,将△ABC的三边缩小的原来的 ,如图,任取一点O , 连AO、BO、CO , 并取它们的中点D、E、F , 得△DEF , 则下列说法正确的个数是( )
A、 B、 C、 D、10. 按如下方法,将△ABC的三边缩小的原来的 ,如图,任取一点O , 连AO、BO、CO , 并取它们的中点D、E、F , 得△DEF , 则下列说法正确的个数是( )①△ABC与△DEF是位似图形②△ABC与△DEF是相似图形③△ABC与△DEF的周长比为1:2④△ABC与△DEF的面积比为4:1.
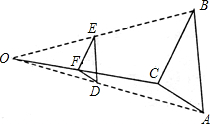 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,以点O为位似中心,将 放大后得到 , ,则 .
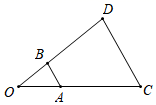 12. 如图,△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形,且 = ,已知点A(﹣1,0),点C( ,1),则A'C'=.
12. 如图,△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形,且 = ,已知点A(﹣1,0),点C( ,1),则A'C'=.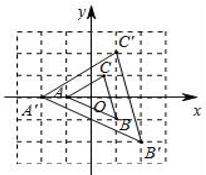 13. 如图, 与 是以坐标原点 为位似中心的位似图形,若点 , , 则 的面积为.
13. 如图, 与 是以坐标原点 为位似中心的位似图形,若点 , , 则 的面积为.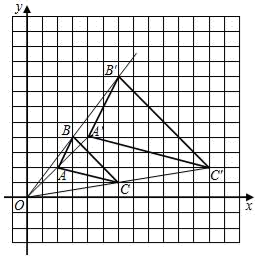 14. 如图,△AOB三个顶点的坐标分别为A(8,0),O(0,0),B(8,﹣6),点M为OB的中点.以点O为位似中心,把△AOB缩小为原来的 ,得到△A′O′B′,点M′为O′B′的中点,则MM′的长为 .
14. 如图,△AOB三个顶点的坐标分别为A(8,0),O(0,0),B(8,﹣6),点M为OB的中点.以点O为位似中心,把△AOB缩小为原来的 ,得到△A′O′B′,点M′为O′B′的中点,则MM′的长为 .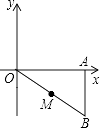 15. 如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
15. 如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).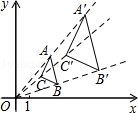
①若点A( ,3),则A′的坐标为;
②△ABC与△A′B′C′的相似比等于;
③若△ABC的面积为m,则△A′B′C′的面积= .
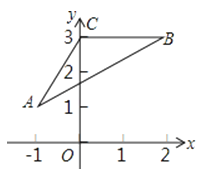
16.如图,在直角坐标系中,△ABC的各顶点坐标为A(﹣1,1),B(2,3),C(0,3).现以坐标原点为位似中心,作△A′B′C′,使△A′B′C′与△ABC的位似比为 . 则点A的对应点A′的坐标为
 17. 如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为 .
17. 如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为 .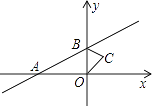 18.
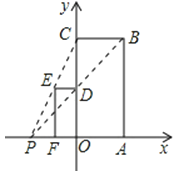
18.如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(﹣1,2),则点P的坐标为
三、作图题
-
19. 如图,四边形ABCD各顶点的坐标分别为A(2,6),B(4,2),C(6,2),D(6,4),
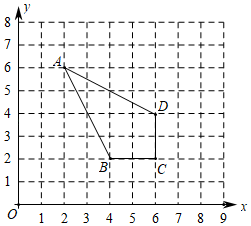
①在第一象限内,画出以原点为位似中心,相似比为 的位似图形A1B1C1D1;
②将四边形A1B1C1D1向右平移5个单位长度,再向上平移4个单位长度,并写出各点坐标.
四、解答题
-
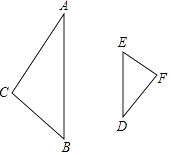
20. 如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,请确定点O的位置,如果OC=3.6cm,OF=2.4cm,求它们的相似比.
 21. 方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示,
21. 方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示,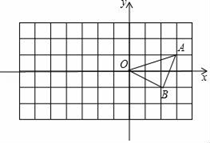
解答问题:
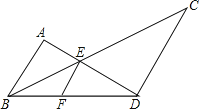
(1)、请按要求对△OAB作变换:以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△OA′B′.(2)、写出点A′的坐标;(3)、求△OA′B'的面积.22.如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,
(1)图中有哪几对位似三角形,选其中一对加以证明;
(2)若AB=2,CD=3,求EF的长.
 23.
23.如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
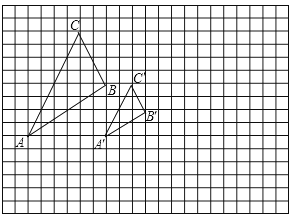 (1)、画出位似中心点O;(2)、直接写出△ABC与△A′B′C′的位似比;(3)、以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.24.
(1)、画出位似中心点O;(2)、直接写出△ABC与△A′B′C′的位似比;(3)、以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.24.如图,△ABC中,AD、BE是高.
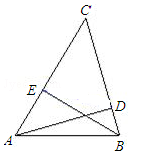 (1)、求证:;(2)、连接DE,那么△CDE与△CAB是位似图形吗?25.
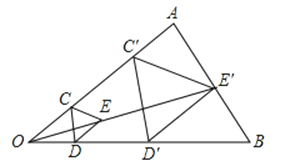
(1)、求证:;(2)、连接DE,那么△CDE与△CAB是位似图形吗?25.如图,用下面的方法可以画△AOB的内接等边三角形,阅读后解答相应问题.
画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上;②连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E′D′∥ED,交OB于点D′;③连接C′D′,则△C′D′E′是△AOB的内接等边三角形.
(1)求证:△C′D′E′是等边三角形;
(2)求作:内接于已知△ABC的矩形DEFG,使它的边EF在BC上,顶点D,G分别在AB,AC上,且DE:EF=1:2.
-