初中数学青岛版九年级上学期 第1章 1.3相似三角形的性质
试卷更新日期:2020-08-12 类型:同步测试
一、单选题
-
1. 两个相似三角形对应高之比为 ,那么它们的对应中线之比为( )A、 B、 C、 D、2. 如图,三角形ABC中,D,E分别为边AB,AC上的一点,且DE平行于BC,S△ADE=S四边形DECB , 则△ABC与△ADE相似比的值为( )
 A、2 B、4 C、 D、3. 在相同的时刻,太阳光下物高与影长成正比.如果高为1.5米的人的影长为2.5米,那么影长为30米的旗杆的高是( )A、18米 B、16米 C、20米 D、15米4. 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
A、2 B、4 C、 D、3. 在相同的时刻,太阳光下物高与影长成正比.如果高为1.5米的人的影长为2.5米,那么影长为30米的旗杆的高是( )A、18米 B、16米 C、20米 D、15米4. 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )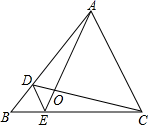 A、 B、 C、 D、5. 如右图,矩形EFGH内接于△ABC,且边FG落在BC上,如果AD⊥BC,BC=3,AD=2,EF:EH=2:3,那么EH的长为( )
A、 B、 C、 D、5. 如右图,矩形EFGH内接于△ABC,且边FG落在BC上,如果AD⊥BC,BC=3,AD=2,EF:EH=2:3,那么EH的长为( )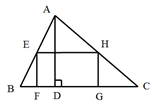 A、 B、 C、 D、26. 如图,在△ABC中,AB=AC=8,BC=6,点P从点B出发以1个单位/s的速度向点A运动,同时点Q从点C出发以2个单位/s的速度向点B运动.当以B,P,Q为顶点的三角形与△ABC相似时,运动时间为( )
A、 B、 C、 D、26. 如图,在△ABC中,AB=AC=8,BC=6,点P从点B出发以1个单位/s的速度向点A运动,同时点Q从点C出发以2个单位/s的速度向点B运动.当以B,P,Q为顶点的三角形与△ABC相似时,运动时间为( ) A、 s B、 s C、 s或 s D、以上均不对7. 如图,在△ABC中,E,G分别是AB,AC上的点,∠AEG=∠C,∠BAC的平分线AD交EG于点F,若 ,则( )
A、 s B、 s C、 s或 s D、以上均不对7. 如图,在△ABC中,E,G分别是AB,AC上的点,∠AEG=∠C,∠BAC的平分线AD交EG于点F,若 ,则( )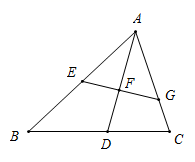 A、 B、 C、 D、8. 如图,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长于点Q,下列结论正确的有( )个.
A、 B、 C、 D、8. 如图,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长于点Q,下列结论正确的有( )个.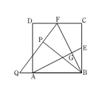
①AE⊥BF; ②QB=QF; ③ ; ④SECPG=3S△BGE
A、1 B、4 C、3 D、29. 在 中,点 在 上,点 在 上,且 与 相似, , , ,则 的长为( )A、 B、12 C、 D、 或10. 如图,P是 ABCD内一点,连结P与 ABCD各顶点, EFGH各顶点分别在边AP、BP、CP、DP上,且AE=2EP,EF∥AB.若△PEF与△PGH的面积和为1,则 ABCD的面积为( )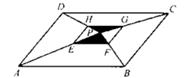 A、4 B、6 C、12 D、18
A、4 B、6 C、12 D、18二、填空题
-
11. 两个相似三角形的相似比为1:3,则它们周长的比为 .12. 如图,在△ABC中,AB=4,AC=3,D是AB边上的一点.若△ABC∽△ACD,则AD的长为.
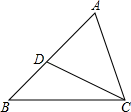 13. 如图,△ABC 的 两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么 =.
13. 如图,△ABC 的 两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么 =. 14. 如图,在 中,已知 , ,垂足为D, .若 是 的中点,则 .
14. 如图,在 中,已知 , ,垂足为D, .若 是 的中点,则 .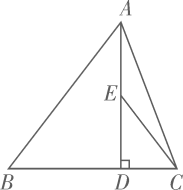 15. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形,如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是.
15. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形,如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是.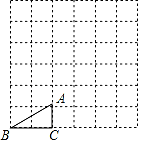 16. 如图,AD与BC相交于E,点F在BD上,且AB∥EF∥CD,若EF=2,CD=3,则AB的长为.
16. 如图,AD与BC相交于E,点F在BD上,且AB∥EF∥CD,若EF=2,CD=3,则AB的长为. 17. 如图,矩形ABCD中,DE⊥AC于点F,交BC边于点E,已知AB=6,AD=8,则CE的长为.
17. 如图,矩形ABCD中,DE⊥AC于点F,交BC边于点E,已知AB=6,AD=8,则CE的长为.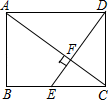 18. 如图,在□ 中, 是一条对角线, ,且 与 相交于点 ,与 相交于点 , ,连接 .若 ,则 的值为 .
18. 如图,在□ 中, 是一条对角线, ,且 与 相交于点 ,与 相交于点 , ,连接 .若 ,则 的值为 .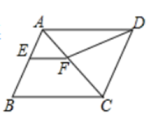
三、作图题
-
19. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上。
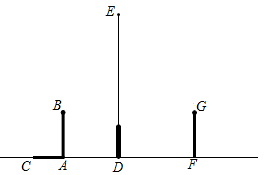 (1)、请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子。(用线段表示)(2)、如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高。
(1)、请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子。(用线段表示)(2)、如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高。四、解答题
-
20. 在古代的《九章算术》中有一道题:今有勾五步,股 步,问勾中容方几何?意思是:如图,在 中,短直角边 步,长直角边 步,正方形有两边在两直角边上,一个顶点在斜边上.这个正方形 的边长为多少?
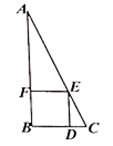 21. 如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己得影长FG=4m,如果小明的身高为1.6m,求路灯杆AB的高度.
21. 如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己得影长FG=4m,如果小明的身高为1.6m,求路灯杆AB的高度.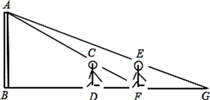 22. 如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端,视线所及如图①所示。根据实际情况画出平面图形如图②,CD⊥DF,AB⊥DF,EF⊥DF,甲从点C可以看到点G处,乙从点E恰巧可以看到点D处,点B是DF的中点,路灯AB高5.5米,DF=120米,BG=10.5米,求甲、乙两人的观测点到地面的距离的差。
22. 如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端,视线所及如图①所示。根据实际情况画出平面图形如图②,CD⊥DF,AB⊥DF,EF⊥DF,甲从点C可以看到点G处,乙从点E恰巧可以看到点D处,点B是DF的中点,路灯AB高5.5米,DF=120米,BG=10.5米,求甲、乙两人的观测点到地面的距离的差。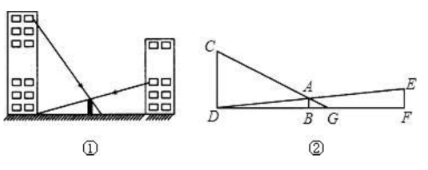 23. 如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长.
23. 如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长. 24. 问题探究:三角形的角平分线是初中几何中一条非常重要的线段,它除了具有平分角、角平分线上的点到角两边的距离相等这些性质外,还具有以下的性质:
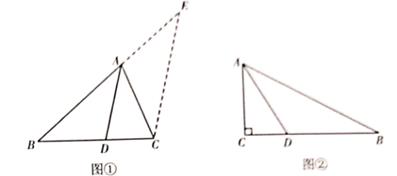
24. 问题探究:三角形的角平分线是初中几何中一条非常重要的线段,它除了具有平分角、角平分线上的点到角两边的距离相等这些性质外,还具有以下的性质:如图①,在△ABC中,AD平分∠BAC交BC于点D,则 。
提示:过点C作CE∥AD交BA的延长线于点E。
请根据上面的提示,写出得到“ “这一结论完整的证明过程。
结论应用:如图②2,在Rt△ABC中,∠C=90°,AC=8,BC=15,AD平分∠BAC交BC于点D。请直接利用“问题探究”的结论,求线段CD的长。
 25. 已知:如图,在正方形ABCD中,Q是CD的中点, 求证: .
25. 已知:如图,在正方形ABCD中,Q是CD的中点, 求证: .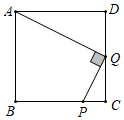 26. 净觉寺享有“家东第一寺”的美誉,是一座规模较大,布局严颜,结构合理,独具一格的古建筑群体,被国务院批准列入第六批全国重点文物保护单位名单,某校社会实践小组为了测量寺内一古塔的高度,在地面上 处垂直于地面竖立了高度为 米的标杆 ,这时地面上的点 ,标杆的顶端点 ,古塔的塔尖点 正好在同一直线上,测得 米,将标杆向后平移到点处,这时地面上的点 ,标杆的顶端点 ,古塔的塔尖点 正好在同一直线上(点 ,点 ,点 ,点 与古塔底处的点 在同一直线上)这时测得 米, 米,请你根据以上数据,计算古塔的高度 .
26. 净觉寺享有“家东第一寺”的美誉,是一座规模较大,布局严颜,结构合理,独具一格的古建筑群体,被国务院批准列入第六批全国重点文物保护单位名单,某校社会实践小组为了测量寺内一古塔的高度,在地面上 处垂直于地面竖立了高度为 米的标杆 ,这时地面上的点 ,标杆的顶端点 ,古塔的塔尖点 正好在同一直线上,测得 米,将标杆向后平移到点处,这时地面上的点 ,标杆的顶端点 ,古塔的塔尖点 正好在同一直线上(点 ,点 ,点 ,点 与古塔底处的点 在同一直线上)这时测得 米, 米,请你根据以上数据,计算古塔的高度 .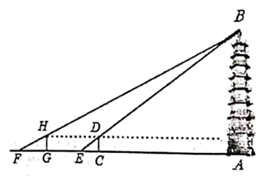
-