广东省潮州市湘桥区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-08-11 类型:期末考试
一、选择题(每小题3分,共30分)
-
1. 中国上海世博会吉祥物的名字叫“海宝”,意即“四海之宝”。通过平移,可将图中的吉祥物“海宝”平移到图( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 点P(-4,3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图所示,直线a,b相交于点O,若∠1等于50°,则∠2等于( )
2. 点P(-4,3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图所示,直线a,b相交于点O,若∠1等于50°,则∠2等于( )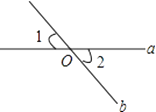 A、50° B、40° C、140° D、130°4. 下列调查中,最适合采用全面调查的是( )A、端午节期间市场上粽子质量 B、了解CCTV1电视剧《麦香》的收视率 C、调查我校某班学生喜欢上数学课的情况 D、菜品牌手机的防水性能5. 16的算术平方根是( )A、±4 B、4 C、8 D、±86. 在平面直角坐标系中,将点(-2,3)向上平移1个单位长度,所得到的点的坐标是( )A、(-1,3) B、(-2,2) C、(-2,4) D、(-3,3)7. 如图,不等式组 的解集在数轴上表示正确的是( )A、
A、50° B、40° C、140° D、130°4. 下列调查中,最适合采用全面调查的是( )A、端午节期间市场上粽子质量 B、了解CCTV1电视剧《麦香》的收视率 C、调查我校某班学生喜欢上数学课的情况 D、菜品牌手机的防水性能5. 16的算术平方根是( )A、±4 B、4 C、8 D、±86. 在平面直角坐标系中,将点(-2,3)向上平移1个单位长度,所得到的点的坐标是( )A、(-1,3) B、(-2,2) C、(-2,4) D、(-3,3)7. 如图,不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、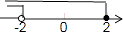 D、
D、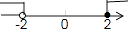 8. 下列各式正确的是( )A、 =-2 B、 =3 C、 =-4 D、 =±59. 已知a>b,下列不等式变形不正确的是( )A、a+2>b+2 B、a-2>b-2 C、2a>2b D、2-a>2-b10. 我国明代数学家程大位的名著《直接算法统宗》里有一道著名算题,意思是:有100个和尚分100个馒头,如果大和尚一人分3个,小和尚3人分一个,正好分完,试问大、小和尚各几人?若设大、小和尚各有x,y人,下列方程组正确的是( )A、 B、 C、 D、
8. 下列各式正确的是( )A、 =-2 B、 =3 C、 =-4 D、 =±59. 已知a>b,下列不等式变形不正确的是( )A、a+2>b+2 B、a-2>b-2 C、2a>2b D、2-a>2-b10. 我国明代数学家程大位的名著《直接算法统宗》里有一道著名算题,意思是:有100个和尚分100个馒头,如果大和尚一人分3个,小和尚3人分一个,正好分完,试问大、小和尚各几人?若设大、小和尚各有x,y人,下列方程组正确的是( )A、 B、 C、 D、二、填空题(每小题4分,共24分)
-
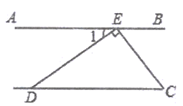
11. “x与3的和是非负数”用不等式表示为。12. 点 点在第四象限,且点 到 轴、 轴的距离分别为6、8,则点 的坐标为.13. 如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为。
 14. 比较大小: 0.5(选填“>”、”<”或“=“)。15. 为了了解班中学生每月的零花钱,某班5名同学记录了自己一周的零花钱分别是:12,9,10,11,13(单位:元),如果该班有50名学生,估计全班同学一周的零花钱约为元。16. 若 是方程x-2y=0的解,则3a-6b+2=。
14. 比较大小: 0.5(选填“>”、”<”或“=“)。15. 为了了解班中学生每月的零花钱,某班5名同学记录了自己一周的零花钱分别是:12,9,10,11,13(单位:元),如果该班有50名学生,估计全班同学一周的零花钱约为元。16. 若 是方程x-2y=0的解,则3a-6b+2=。三、解答题(每小题6分,共30分)
-
17. 利用平方根的定义解方程:2x2-50=018. 计算:19. 计算:20. 解方程组:21. 解不等式: >1,并把解集在数轴上表示出来:

四、解答题(每小题8分,共16分)
-
22. 学习了统计知识后,小刚就本班同学的上学方式进行了一次调查统计。图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图。请你根据图中提供的信息,解答以下问题:
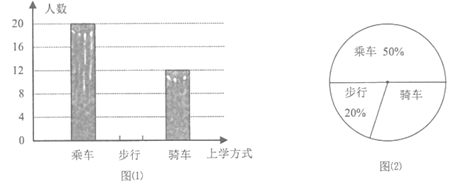 (1)、该班共有名学生,并把条形图补充完整;(2)、在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数。(3)、如果全年级共500名同学,请你估算全年级步行上学的学生人数。23. △ABC与△A1B1C1在平面直角坐标系中的位置如图所示
(1)、该班共有名学生,并把条形图补充完整;(2)、在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数。(3)、如果全年级共500名同学,请你估算全年级步行上学的学生人数。23. △ABC与△A1B1C1在平面直角坐标系中的位置如图所示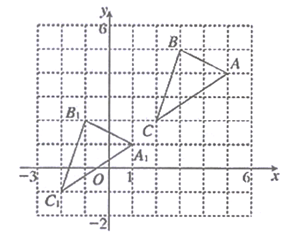 (1)、分别写出下列各点的坐标:A;C;C1;(2)、△A1B1C1由△ABC经过怎样的平移得到?(3)、若点P(a+4,a+4)是△ABC内部一点,则△A1B1C1内部的对应点P1恰好在x轴上,那么P1坐标为;(4)、求△ABC面积。
(1)、分别写出下列各点的坐标:A;C;C1;(2)、△A1B1C1由△ABC经过怎样的平移得到?(3)、若点P(a+4,a+4)是△ABC内部一点,则△A1B1C1内部的对应点P1恰好在x轴上,那么P1坐标为;(4)、求△ABC面积。五、解答题(每小题10分,共20分)
-
24. 今年夏天,我州某地区遭受罕见的水灾,“水灾无情人有情”,州里某单位给该地区某中学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件。(1)、求饮用水和蔬菜各有多少件。(2)、现计划租用甲、乙两种型号的货车共8辆,一次性将这批饮用水和蔬菜全部运往受灾地区某中学。已知每辆甲型货车最多可装饮用水40件和蔬菜10件,每辆乙型货车最多可装饮用水和蔬菜各20件,则该单位安排甲、乙两种货车时有几种方案?请你帮忙设计出来。(3)、在(2)的条件下,如果甲型货车每辆需付运费400元,乙型货车每辆需付运费360元。该单位应选择哪种方案可使运费最少?最少运费是多少元?25. 如图
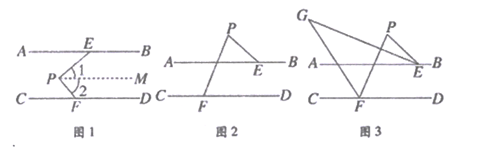 (1)、如图1,AB∥CD,∠AEP=40°,∠PFD=130°。求∠EPF的度数。
(1)、如图1,AB∥CD,∠AEP=40°,∠PFD=130°。求∠EPF的度数。小明想到了以下方法(不完整),请填写以下结论的依据:
如图1,过点P作PM∥AB,
∴∠1=∠AEP=40°()
∵AB∥CD,(已知)
∴PM∥CD,()
∠2+∠PFD=180°()
∵∠PFD=130°,∴∠2=180°-130°=50°
∴∠1+∠2=40°+50°=90°
即∠EPF=90°
(2)、如图2,AB∥CD,点P在AB,CD外,问∠PEA,∠PFC,∠P之间有何数量关系?请说明理由;(3)、如图3所示,在(2)的条件下,已知∠P=α,∠PEA的平分线和ZPFC的平分线交于点G,用含有α的式子表示∠G的度数是。(直接写出答案,不需要写出过程)