2021高考一轮复习第二十一讲平面向量的数量积与平面向量应用举例

试卷更新日期：2020-08-11 类型：一轮复习

进入出卷网下载

一、单选题

1. 已知向量a，b满足 $| \vec{a} | = 5$ ， $| \vec{b} | = 6$ ， $\vec{a} \cdot \vec{b} = - 6$ ，则 $\cos ⟨ \vec{a}, \vec{a} + \vec{b} ⟩ =$ （）

A、 $- \frac{31}{35}$ B、 $- \frac{19}{35}$ C、 $\frac{17}{35}$ D、 $\frac{19}{35}$

查看试题解析
2. 已知向量 $\vec{a}$ 、 $\vec{b}$ 满足 $| \vec{a} | = 1, | \vec{b} | = 2, | 2 \vec{a} - \vec{b} | = 2$ ，则向量 $\vec{a}$ ， $\vec{b}$ 的夹角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{π}{4}$ D、 $\frac{π}{2}$

查看试题解析
3. 已知向量 $\vec{a}$ 在 $\vec{b}$ 方向上的投影为 $- 2$ ，且 $(\vec{a} + \vec{b}) \cdot \vec{b} = - 1$ ，则 $\vec{a} \cdot \vec{b} =$ （）

A、2 B、1 C、-1 D、-2

查看试题解析
4. 设 $\vec{a} = (- 1, 3)$ ， $\vec{b} = (1, 1)$ ， $\vec{c} = \vec{a} + k \vec{b}$ ，若 $\vec{b} ⊥ \vec{c}$ ，则 $\vec{a}$ 与 $\vec{c}$ 的夹角余弦值为（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{2 \sqrt{2}}{3}$

查看试题解析
5. 已知 $\vec{a} ， \vec{b}$ 为不共线的两个单位向量，且 $\vec{a}$ 在 $\vec{b}$ 上的投影为 $- \frac{1}{2}$ ，则 $| 2 \vec{a} - \vec{b} | =$ （）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{6}$ D、 $\sqrt{7}$

查看试题解析
6. 已知向量 $\vec{a}$ ， $\vec{b}$ 满足| $\vec{a}$ |＝1，| $\vec{b}$ |＝2，且 $\vec{a}$ 与 $\vec{b}$ 的夹角为120°，则 $| \vec{a} - 3 \vec{b} |$ ＝（）

A、 $\sqrt{11}$ B、 $\sqrt{37}$ C、 $2 \sqrt{10}$ D、 $\sqrt{43}$

查看试题解析
7. 已知 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 分别为直角坐标系 $x O y$ 的 $x, y$ 轴正上方上单位向量， $\vec{A C} = 4 \vec{e_{1}} - 3 \vec{e_{2}}$ ， $\vec{B D} = 6 \vec{e_{1}} + 8 \vec{e_{2}}$ ，则平行四边形 $A B C D$ 的面积为（）

A、25 B、50 C、75 D、100

查看试题解析
8. 已知平面向量 $\overset{⇀}{a}$ ， $\overset{⇀}{b}$ 是非零向量，| $\overset{⇀}{a}$ |=2， $\overset{⇀}{a}$ ⊥( $\overset{⇀}{a}$ +2 $\overset{⇀}{b}$ )，则向量 $\overset{⇀}{b}$ 在向量 $\overset{⇀}{a}$ 方向上的投影为（）

A、1 B、-1 C、2 D、-2

查看试题解析
9. 已知向量 $\overset{⇀}{B A}$ ＝(4，－3)，向量 $\overset{⇀}{B C}$ ＝(2，－4)，则△ABC的形状为（）

A、等腰非直角三角形 B、等边三角形 C、直角非等腰三角形 D、等腰直角三角形

查看试题解析
10. 设向量 $\overset{⇀}{a} = (3, \frac{15}{2})$ ， $\overset{⇀}{b} = (x, \frac{2}{3})$ ，若 $\overset{⇀}{a}$ 与 $\overset{⇀}{b}$ 的夹角为锐角，则实数x的取值范围是（）

A、 $(- \frac{5}{3}, + \infty)$ B、 $(\frac{4}{15}, + \infty)$ C、 $(- \frac{5}{3}, \frac{4}{15}) \cup (\frac{4}{15}, + \infty)$ D、 $(- \infty, \frac{4}{15}) \cup (\frac{5}{3}, + \infty)$

查看试题解析
11. 在边长为2的正方形ABCD中，E，F分别为BC和DC的中点，则 $\vec{A E} \cdot \vec{A F} =$ （）

A、 $\frac{5}{2}$ B、 $- \frac{5}{2}$ C、4 D、-4

查看试题解析
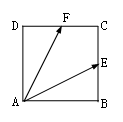12. 若a，b，c均为实数，则下面三个结论均是正确的：
① $a b = b a$ ；② $(a b) c = a (b c)$ ；③若 $a b = b c$ ， $b \neq 0$ ，则 $a - c = 0$ ；

对向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ ，用类比的思想可得到以下四个结论：

① $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$ ；② $(\vec{a} \cdot \vec{b}) \vec{c} = \vec{a} (\vec{b} \cdot \vec{c})$ ；③若 $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{c}$ ， $\vec{b} \neq 0$ ，则 $\vec{a} = \vec{c}$ ；

其中结论正确的有（）

A、1个 B、2个 C、3个 D、0个

查看试题解析

二、填空题

13. 设向量 $a = (1, - 1), b = (m + 1, 2 m - 4)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $m =$ .

查看试题解析
14. 已知点M是边长为2的正 $△ A B C$ 内一点，且 $\vec{A M} = λ \vec{A B} + μ \vec{A C}$ ，若 $λ + μ = \frac{1}{3}$ ，则 $\vec{M B} \cdot \vec{M C}$ 的最小值为.

查看试题解析
15. 在 $△ A B C$ 中， $\vec{A B} = (\sqrt{3} \cos x ， \cos x) ， \vec{A C} = (\cos x ， \sin x)$ ，则 $△ A B C$ 面积的最大值是

查看试题解析
16. 已知向量 $\vec{a} =$ （1，2）， $\vec{b} =$ （2，﹣2），|2 $\vec{a} + \vec{b}$ |＝， $\vec{a}$ 在 $\vec{b}$ 方向上的投影为.

查看试题解析
17. 在锐角 $△ A B C$ 中，点 $D$ 、 $E$ 、 $F$ 分别在边 $A B$ 、 $B C$ 、 $C A$ 上，若 $\vec{A B} = 3 \vec{A D}$ ， $\vec{A C} = λ \vec{A F}$ ，且 $\vec{B C} \cdot \vec{E D} = 2 \vec{E F} \cdot \vec{E D} = 6$ ， $| \vec{E D} | = 1$ ，则实数 $λ$ 的值为．

查看试题解析
18. 如图，在四边形ABCD中，AB⊥BC，AB=6，BC=8，△ACD是等边三角形，则 $\overset{⇀}{A C} \cdot \overset{⇀}{B D}$ 的值为．

查看试题解析
19. 如图，在四边形 $A B C D$ 中， $∠ B = 60^{°} ， A B = 3$ ， $B C = 6$ ，且 $\vec{A D} = λ \vec{B C} ， \vec{A D} \cdot \vec{A B} = - \frac{3}{2}$ ，则实数 $λ$ 的值为，若 $M ， N$ 是线段 $B C$ 上的动点，且 $| \vec{M N} | = 1$ ，则 $\vec{D M} \cdot \vec{D N}$ 的最小值为．

查看试题解析
20. 已知正方形 $A B C D$ 的边长为2，点P满足 $\vec{A P} = \frac{1}{2} (\vec{A B} + \vec{A C})$ ，则 $| \vec{P D} | =$ ； $\vec{P B} \cdot \vec{P D} =$ ．

查看试题解析
21. 设 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 为单位向量，满足|2 $\vec{e_{1}}$ ﹣ $\vec{e_{2}}$ |≤ $\sqrt{2}$ ， $\vec{a}$ ＝ $\vec{e_{1}}$ + $\vec{e_{2}}$ ， $\vec{b}$ ＝3 $\vec{e_{1}}$ + $\vec{e_{2}}$ ，设 $\vec{a}$ ， $\vec{b}$ 的夹角为θ，则cos²θ的最小值为．

查看试题解析

三、解答题

22. 已知向量 $\vec{a} = (\sin x ， \frac{3}{4})$ ， $\vec{b} = (\cos x ， - 1)$ .

(1)、当 $\vec{a} / / \vec{b}$ 时，求 $\tan 2 x$ 的值；

(2)、设函数 $f (x) = 2 (\vec{a} + \vec{b}) \cdot \vec{b}$ ，且 $x \in (0 ， \frac{π}{2})$ ，求 $f (x)$ 的最大值以及对应的x的值.

查看试题解析
23. 已知向量 $\vec{a} = (m \sin x, \cos x)$ ， $\vec{b} = (\sin x, m \sin x)$ ， $x \in (0, \frac{π}{2})$ .

(1)、若 $\vec{a} / / \vec{b}$ ， $\tan x = \frac{1}{4}$ ，求实数m的值；

(2)、记 $f (x) = \vec{a} \cdot \vec{b}$ ，若 $f (x) \geq - \frac{1}{2}$ 恒成立，求实数m的取值范围.

查看试题解析
24. 已知向量 $\vec{a} = (\cos \frac{3 x}{2}, \sin \frac{3 x}{2}), \vec{b} = (\cos \frac{x}{2}, - \sin \frac{x}{2}), x \in [- \frac{π}{3}, \frac{π}{4}]$ 求

(1)、求 $| \overset{⇀}{a} + \overset{⇀}{b} |$ ；

(2)、若 $f (x) = \overset{⇀}{a} \cdot \overset{⇀}{b} - | \overset{⇀}{a} + \overset{⇀}{b} |$ ，求 $f (x)$ 的最大值和最小值

查看试题解析

2021高考一轮复习 第二十一讲 平面向量的数量积与平面向量应用举例

一、单选题

二、填空题

三、解答题

2021高考一轮复习第二十一讲平面向量的数量积与平面向量应用举例