初中数学北师大版九年级上学期 第一章 3 正方形的性质与判定
试卷更新日期：2020-08-11 类型：同步测试
一、单选题
-
1. 下列命题是假命题的是（ ）A、平行四边形的对角线互相平分 B、矩形的对角线互相垂直 C、菱形的对角线互相垂直平分 D、正方形的对角线互相垂直平分且相等2. 如图，四边形 是正方形，O ， D两点的坐标分别是 ， ，点C在第一象限，则点C的坐标是（ ）
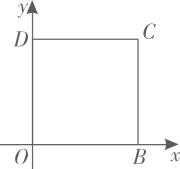A、 B、 C、 D、3. 如图，正方形ABCD的边长为1，点P为BC上任意一点（可与点B或C重合），分别过B、C、D作射线AP的垂线，垂足分别是B′、C′、D′，则BB′＋CC′＋DD′的最小值是（ ）
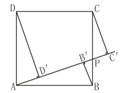A、1 B、 C、 D、4. 如图，小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB＝BC，②∠ABC＝90°，③AC＝BD，④AC⊥BD中任选两个作为补充条件，使▱ABCD为正方形.现有下列四种选法，你认为其中错误的是（ ）
A、②③ B、①③ C、①② D、③④5. 如图，在正方形 中，点 是 的中点，点 是 的中点， 与 相交于点 ，设 .得到以下结论：① ；② ；③ 则上述结论正确的是（ ）
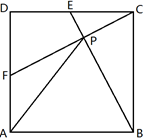A、①② B、①③ C、②③ D、①②③6. 如图①，正方形 中， ， 相交于点O，E是 的中点，动点P从点E出发，沿着 的路径以每秒1个单位长度的速度运动到点A，在此过程中线段 的长度 随着运动时间x的函数关系如图②所示，则 的长为（ ）
A、 B、4 C、 D、7. 如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH . 连结EG，BD相交于点O，BD与HC相交于点P.若GO=GP，则 的值是（ ）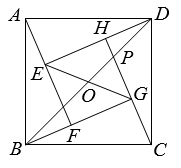
A、 B、 C、 D、二、填空题
-
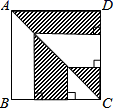
8. 要使一个平行四边形成为正方形，则需添加的条件为（填上一个正确的结论即可）.9. 如图，正方形ABCD的边长为4厘米，则图中阴影部分的面积为.
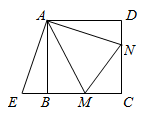
10. 如图，在△ABC中，分别以AB，AC为边向外作正方形ABED，ACGF。若点E，A，G在同一直线上，EG=8 ，BC=7，则△ABC的面积为。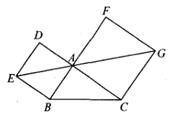
11. 如图，四边形ACDF是正方形，∠CEA和∠ABF都是直角且点E，A，B三点共线，AB=4，则阴影部分的面积是 。
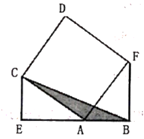12. 如图，在边长为 的正方形 中，点 分别是边 的中点，连接 点 分别是 的中点，连接 ，则 的长度为.
13. 用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖面积为a，小正方形地砖面积为b. 依次连接四块大正方形地砖的中心得到正方形ABCD. 则正方形ABCD的面积为. （用含a，b的代数式表示）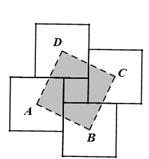
三、综合题
-
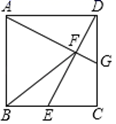
14. 如图，在正方形ABCD中，点E是AB边上的一点，以DE为边作正方形DEFG，DF与BC交于点M，延长EM交GF于点H，EF与GB交于点N，连接CG.
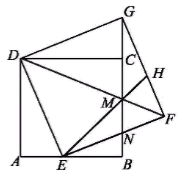(1)、求证：CD⊥CG；(2)、若tan∠MEN= ，求 的值；(3)、已知正方形ABCD的边长为1，点E在运动过程中，EM的长能否为 ？请说明理由.
