初中数学北师大版九年级上学期 第一章 1 菱形的性质与判定
试卷更新日期：2020-08-11 类型：同步测试
一、单选题
-
1. 菱形不具备的性质是（ ）A、是轴对称图形 B、是中心对称图形 C、对角线互相垂直 D、对角线一定相等2. 如图，▱ABCD的对角线AC、BD相交于点O，那么下列条件中，能判断▱ABCD是菱形的为（ ）
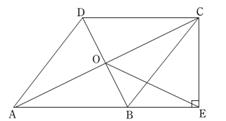
A、AO＝CO B、AO＝BO C、∠AOB＝∠BOC D、∠BAD＝∠ABC3. 如图，在菱形ABCD中，AB＝5，AC＝6，过点D作DE⊥BA，交BA的延长线于点E，则线段DE的长为（ ）
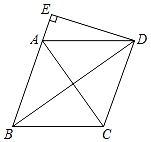A、 B、 C、4 D、4. 如图，已知在平面直角坐标系中，四边形ABCD是菱形，其中B点坐标是(8，2)，D点坐标是(0，2)，点A在x轴上，则菱形ABCD的周长是（ ）
A、2 B、8 C、8 D、125. 如图，菱形ABCD的对角线AC、BD相交于点O.若周长为20，BD＝8，则AC的长是（ ）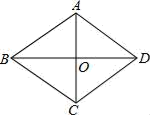
A、3 B、4 C、5 D、66. 如图，在菱形ABCD中，M、N分别在AD、BC上，且AM=CN，连接MN与AC交于点O，连接BO，若∠DAC=28°，则∠OBC的度数为（ ）
A、28° B、56° C、62° D、72°二、填空题
-
7. 如图， ABCD的对角线AC，BD相交于点O，请添加一个条件： ， 使 ABCD是菱形。
8. 已知菱形的边长为4，一个内角为60°，则菱形较短的对角线长为 ．9. 如图，菱形ABCD的边长为4，∠B＝120°.点P是对角线AC上一点（不与端点A重合），则线段 AP+PD的最小值为.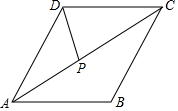
三、解答题
-
10. 如图，矩形ABCD中，对角线AC、BD交于点O ， 以AD、OD为邻边作平行四边形ADOE ， 连接BE ． 求证：四边形AOBE为菱形．
11. 如图，在正方形 中，点E在 边的延长线上，点F在 边的延长线上，且 ，连接 和 相交于点M．求证： ．
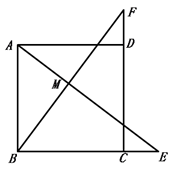12. 已知：如图，在菱形ABCD中，点E，F分别在边BC，CD上，且BE=DF，连结AE，AF.求证：AE=AF.
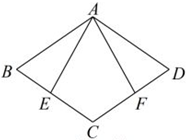13. 如图，菱形ABCD中，E是对角线BD上的一点，连接EA、EC，求证：∠BAE＝∠BCE.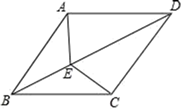
四、综合题
