江苏省盐城2020年中考数学试卷
试卷更新日期:2020-08-10 类型:中考真卷
一、选择题
-
1. 2020的相反数是( )A、 2020 B、﹣2020 C、 D、2. 下列图形中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 实数 在数轴上表示的位置如图所示,则( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 实数 在数轴上表示的位置如图所示,则( ) A、 B、 C、 D、5. 如图是由4个小正方体组合成的几何体,该几何体的俯视图是( )
A、 B、 C、 D、5. 如图是由4个小正方体组合成的几何体,该几何体的俯视图是( ) A、
A、 B、
B、 C、
C、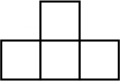 D、
D、 6. 2019年7月盐城黄海湿地中遗成功,它的面积约为400000万平方米,将数据400000用科学记数法表示应为( )A、 B、 C、 D、7. 把 这 个数填入 方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛書”(图 ),是世界上最早的“幻方”.图 是仅可以看到部分数值的“九宫格”,则其中 的值为( )
6. 2019年7月盐城黄海湿地中遗成功,它的面积约为400000万平方米,将数据400000用科学记数法表示应为( )A、 B、 C、 D、7. 把 这 个数填入 方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛書”(图 ),是世界上最早的“幻方”.图 是仅可以看到部分数值的“九宫格”,则其中 的值为( )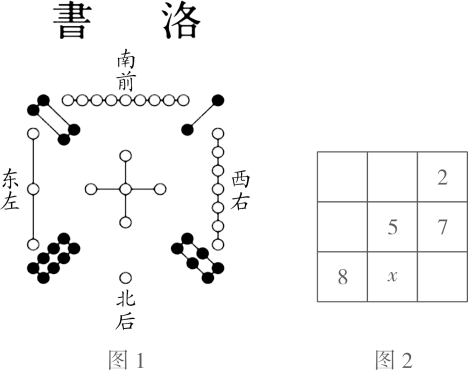 A、1 B、3 C、4 D、68. 如图,在菱形 中,对角线 相交于点 为 中点, .则线段 的长为:( )
A、1 B、3 C、4 D、68. 如图,在菱形 中,对角线 相交于点 为 中点, .则线段 的长为:( ) A、 B、 C、3 D、5
A、 B、 C、3 D、5二、填空题
-
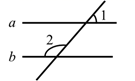
9. 如图,直线 被直线c所截, .那么 .
 10. 一组数据 的平均数为.11. 因式分解: .
10. 一组数据 的平均数为.11. 因式分解: .
12. 分式方程 的解为 .13. 一个不透明的袋中装有3个黑球和2个白球,这些球除颜色外都相同,从这个袋中任意摸出一个球为白球的概率是.14. 如图,在 中,点 在 上, 则 。 15. 如图, 且 ,则 的值为.
15. 如图, 且 ,则 的值为. 16. 如图,已知点 ,直线 轴,垂足为点 其中 ,若 与 关于直线l对称,且 有两个顶点在函数 的图像上,则k的值为:.
16. 如图,已知点 ,直线 轴,垂足为点 其中 ,若 与 关于直线l对称,且 有两个顶点在函数 的图像上,则k的值为:.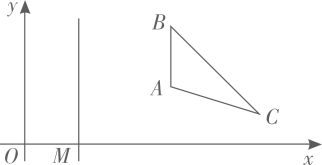
三、解答题
-
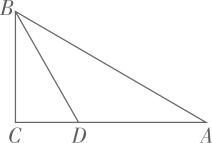
17. 计算: .18. 解不等式组: .19. 先化简,再求值: ,其中 .20. 如图,在 中, 的平分线 交 于点 .求 的长?
 21. 如图,点O是正方形, 的中心.
21. 如图,点O是正方形, 的中心.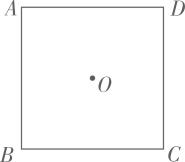 (1)、用直尺和圆规在正方形内部作一点E(异于点O),使得 (保留作图痕迹,不写作法)(2)、连接 求证: .22. 在某次疫情发生后,根据疾控部门发布的统计数据,绘制出如下统计图:图 为A地区累计确诊人数的条形统计图,图 为B地区新增确诊人数的折线统计图.
(1)、用直尺和圆规在正方形内部作一点E(异于点O),使得 (保留作图痕迹,不写作法)(2)、连接 求证: .22. 在某次疫情发生后,根据疾控部门发布的统计数据,绘制出如下统计图:图 为A地区累计确诊人数的条形统计图,图 为B地区新增确诊人数的折线统计图.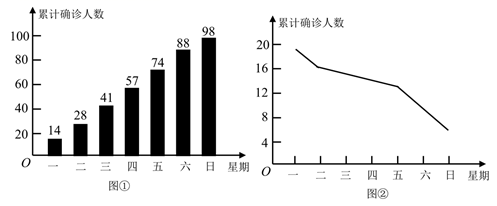 (1)、根据图 中的数据,A地区星期三累计确诊人数为 , 新增确诊人数为;(2)、已知A地区星期一新增确诊人数为14人,在图 中画出表示A地区新增确诊人数的折线统计图.(3)、你对这两个地区的疫情做怎样的分析,推断?23. 生活在数字时代的我们,很多场合用二维码(如图 )来表示不同的信息,类似地,可通过在矩形网格中,对每一个小方格涂加色或不涂色所得的图形来表示不同的信息,例如:网格中只有一个小方格,如图 ,通过涂器色或不涂色可表示两个不同的信息.
(1)、根据图 中的数据,A地区星期三累计确诊人数为 , 新增确诊人数为;(2)、已知A地区星期一新增确诊人数为14人,在图 中画出表示A地区新增确诊人数的折线统计图.(3)、你对这两个地区的疫情做怎样的分析,推断?23. 生活在数字时代的我们,很多场合用二维码(如图 )来表示不同的信息,类似地,可通过在矩形网格中,对每一个小方格涂加色或不涂色所得的图形来表示不同的信息,例如:网格中只有一个小方格,如图 ,通过涂器色或不涂色可表示两个不同的信息. (1)、用树状图或列表格的方法,求图 可表示不同信息的总个数:(图中标号 表示两个不同位置的小方格,下同)
(1)、用树状图或列表格的方法,求图 可表示不同信息的总个数:(图中标号 表示两个不同位置的小方格,下同) (2)、图 为 的网格图.它可表示不同信息的总个数为;
(2)、图 为 的网格图.它可表示不同信息的总个数为;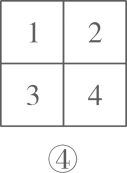 (3)、某校需要给每位师生制作一张“校园出入证”,准备在证件的右下角采用 的网格图来表示各人身份信息,若该校师生共 人,则n的最小值为;24. 如图, 是 的外接圆, 是 的直径, .
(3)、某校需要给每位师生制作一张“校园出入证”,准备在证件的右下角采用 的网格图来表示各人身份信息,若该校师生共 人,则n的最小值为;24. 如图, 是 的外接圆, 是 的直径, .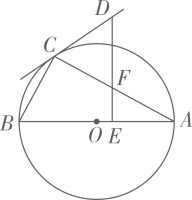 (1)、求证: 是 的切线;(2)、若 ,垂足为 交 与点;求证: 是等腰三角形.25. 若二次函数 的图像与x轴有两个交点 ,且经过点 过点A的直线l与x轴交于点 与该函数的图象交于点B(异于点A).满足 是等腰直角三角形,记 的面积为 的面积为 ,且 .
(1)、求证: 是 的切线;(2)、若 ,垂足为 交 与点;求证: 是等腰三角形.25. 若二次函数 的图像与x轴有两个交点 ,且经过点 过点A的直线l与x轴交于点 与该函数的图象交于点B(异于点A).满足 是等腰直角三角形,记 的面积为 的面积为 ,且 . (1)、抛物线的开口方向(填“上”或“下”);(2)、求直线 相应的函数表达式;(3)、求该二次函数的表达式.26. 木门常常需要雕刻美丽的图案.(1)、图①为某矩形木门示意图,其中 长为200厘米, 长为100厘米,阴影部分是边长为30厘米的正方形雕刻模具,刻刀的位置在模具的中心点P处,在雕刻时始终保持模具的一边紧贴木门的一边,所刻图案如虚线所示,求图案的周长;
(1)、抛物线的开口方向(填“上”或“下”);(2)、求直线 相应的函数表达式;(3)、求该二次函数的表达式.26. 木门常常需要雕刻美丽的图案.(1)、图①为某矩形木门示意图,其中 长为200厘米, 长为100厘米,阴影部分是边长为30厘米的正方形雕刻模具,刻刀的位置在模具的中心点P处,在雕刻时始终保持模具的一边紧贴木门的一边,所刻图案如虚线所示,求图案的周长;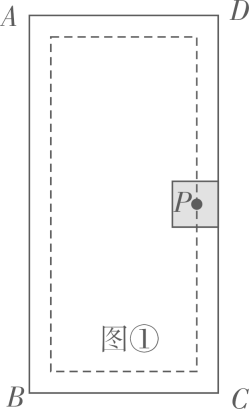 (2)、如图 ,对于(1)中的木门,当模具换成边长为 厘米的等边三角形时,刻刀的位置仍在模具的中心点P处,雕刻时也始终保持模具的一边紧贴本门的一边,使模具进行滑动雕刻.但当模具的一个顶点与木门的一个顶点重合时,需将模具绕着重合点进行旋转雕刻,直到模具的另一边与木门的另一边重合.再滑动模具进行雕刻,如此雕刻一周,请在图 中画出雕刻所得图案的草图,并求其周长.
(2)、如图 ,对于(1)中的木门,当模具换成边长为 厘米的等边三角形时,刻刀的位置仍在模具的中心点P处,雕刻时也始终保持模具的一边紧贴本门的一边,使模具进行滑动雕刻.但当模具的一个顶点与木门的一个顶点重合时,需将模具绕着重合点进行旋转雕刻,直到模具的另一边与木门的另一边重合.再滑动模具进行雕刻,如此雕刻一周,请在图 中画出雕刻所得图案的草图,并求其周长.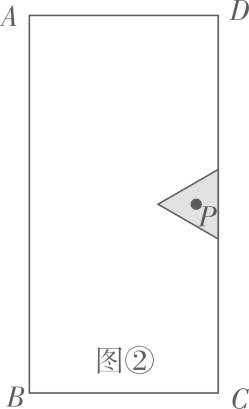 27. 以下虚线框中为一个合作学习小组在一次数学实验中的过程记录,请阅读后完成虚线框下方的问题 .
27. 以下虚线框中为一个合作学习小组在一次数学实验中的过程记录,请阅读后完成虚线框下方的问题 .Ⅰ.在 中, ,在探究三边关系时,通过画图,度量和计算,收集到,组数据如下表:(单位:厘米)
2.8
2.7
2.6
2.3
2
1.5
0.4
0.4
0.8
1.2
1.6
2
2.4
2.8
3.2
3.5
3.8
3.9
4
3.9
3.2
Ⅱ.根据学习函数的经验,选取上表中 和 的数据进行分析;
设 ,以 为坐标,在图 所示的坐标系中描出对应的点;
连线;
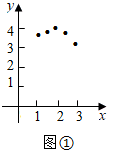
Ⅲ.观察思考
结合表中的数据以及所面的图像,猜想.当 ▲ 时,y最大;
Ⅳ.进一步C猜想:若 中, ,斜边 为常数, ),则 ▲ 时, 最大.
推理证明
Ⅴ.对(4)中的猜想进行证明.
(1)、问题1.在图 中完善(1)的描点过程,并依次连线;(2)、问题2.补全观察思考中的两个猜想:Ⅲ;Ⅳ。(3)、问题3.证明上述Ⅴ中的猜想:(4)、问题4.图 中折线 是一个感光元件的截面设计草图,其中点 间的距离是4厘米, 厘米, 平行光线从 区域射入, 线段 为感光区城,当 的长度为多少时,感光区域长度之和最大,并求出最大值.