湖北省荆州市2020年中考数学试卷
试卷更新日期:2020-08-10 类型:中考真卷
一、选择题
-
1. 有理数 的相反数是( )A、2 B、 C、-2 D、2. 下列四个几何体中,俯视图与其他三个不同的是( )A、
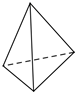 B、
B、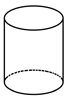 C、
C、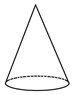 D、
D、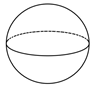 3. 在平面直角坐标系中,一次函数 的图象是( )A、
3. 在平面直角坐标系中,一次函数 的图象是( )A、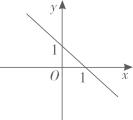 B、
B、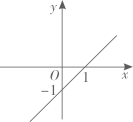 C、
C、 D、
D、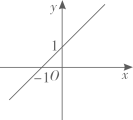 4. 将一张矩形纸片折叠成如图所示的图形,若 ,则 的度数是( )
4. 将一张矩形纸片折叠成如图所示的图形,若 ,则 的度数是( ) A、 B、 C、 D、5. 八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )A、 - =20 B、 - =20 C、 - = D、 =6. 若x为实数,在 的“ ”中添上一种运算符号(在+,-,×,÷中选择)后,其运算的结果是有理数,则x不可能的是( )A、 B、 C、 D、7. 如图,点E在菱形ABCD的AB边上,点F在BC边的延长线上,连接CE,DF,对于下列条件:① ;② ;③ ;④ ,只选其中一个添加,不能确定 的是( )
A、 B、 C、 D、5. 八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )A、 - =20 B、 - =20 C、 - = D、 =6. 若x为实数,在 的“ ”中添上一种运算符号(在+,-,×,÷中选择)后,其运算的结果是有理数,则x不可能的是( )A、 B、 C、 D、7. 如图,点E在菱形ABCD的AB边上,点F在BC边的延长线上,连接CE,DF,对于下列条件:① ;② ;③ ;④ ,只选其中一个添加,不能确定 的是( )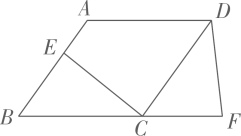 A、① B、② C、③ D、④8. 如图,在平面直角坐标系中, 的斜边OA在第一象限,并与x轴的正半轴夹角为30度,C为OA的中点,BC=1,则A点的坐标为( )
A、① B、② C、③ D、④8. 如图,在平面直角坐标系中, 的斜边OA在第一象限,并与x轴的正半轴夹角为30度,C为OA的中点,BC=1,则A点的坐标为( )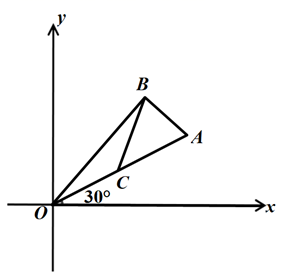 A、 B、 C、 D、9. 定义新运算 ,对于任意实数a,b满足 ,其中等式右边是通常的加法、减法、乘法运算,例如 ,若 (k为实数) 是关于x的方程,则它的根的情况是( )A、有一个实根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根10. 如图,在 正方形网格中,每个小正方形的边长都是1,点A,B,C均在网格交点上,⊙O是 的外接圆,则 的值是( )
A、 B、 C、 D、9. 定义新运算 ,对于任意实数a,b满足 ,其中等式右边是通常的加法、减法、乘法运算,例如 ,若 (k为实数) 是关于x的方程,则它的根的情况是( )A、有一个实根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根10. 如图,在 正方形网格中,每个小正方形的边长都是1,点A,B,C均在网格交点上,⊙O是 的外接圆,则 的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 ,则a,b,c的大小关系是.(用<号连接)12. 若单项式 与 是同类项,则 的值是.13. 已知: ,求作 的外接圆,作法:①分别作线段BC,AC的垂直平分线EF和MN,它们交于点O;②以点O为圆心,OB的长为半径画弧,如图⊙O即为所求,以上作图用到的数学依据是.
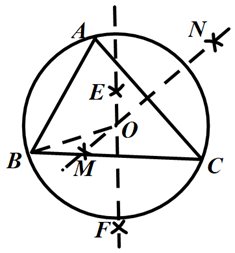 14. 若标有A,B,C的三只灯笼按图示悬挂,每次摘取一只(摘B先摘C),直到摘完,则最后一只摘到B的概率是.
14. 若标有A,B,C的三只灯笼按图示悬挂,每次摘取一只(摘B先摘C),直到摘完,则最后一只摘到B的概率是. 15. “健康荆州,你我同行”,市民小张积极响应“全民健身动起来”号召,坚持在某环形步道上跑步,已知此步道外形近似于如图所示的 ,其中 ,AB与BC间另有步道DE相连,D地在AB的正中位置,E地与C地相距1km,若 ,小张某天沿 路线跑一圈,则他跑了km.
15. “健康荆州,你我同行”,市民小张积极响应“全民健身动起来”号召,坚持在某环形步道上跑步,已知此步道外形近似于如图所示的 ,其中 ,AB与BC间另有步道DE相连,D地在AB的正中位置,E地与C地相距1km,若 ,小张某天沿 路线跑一圈,则他跑了km. 16. 我们约定: 为函数 的关联数,当其图象与坐标轴交点的横、纵坐标均为整数时,该交点为“整交点”,若关联数为 的函数图象与x轴有两个整交点(m为正整数),则这个函数图象上整交点的坐标为.
16. 我们约定: 为函数 的关联数,当其图象与坐标轴交点的横、纵坐标均为整数时,该交点为“整交点”,若关联数为 的函数图象与x轴有两个整交点(m为正整数),则这个函数图象上整交点的坐标为.三、解答题
-
17. 先化简,再求值 :其中a是不等式组 的最小整数解;18. 阅读下列问题与提示后,将解方程的过程补充完整,求出x的值.
问题:解方程 (提示:可以用换元法解方程),
解:设 ,则有 ,
原方程可化为: ,
续解:
19. 如图,将 绕点B顺时针旋转60度得到 ,点C的对应点E恰好落在AB的延长线上,连接AD.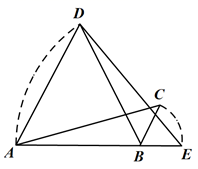 (1)、求证: ;(2)、若AB=4,BC=1,求A,C两点旋转所经过的路径长之和.20. 6月26日是“国际禁毒日”某中学组织七、八年级全体学生开展了“禁毒知识”网上竞赛活动,为了解竞赛情况,从两个年级各抽取10名学生的成绩(满分为100分),收集数据为:七年级90,95,95,80,85,90,85,90,85,100;八年级:85,85,95,80,95,90,90,90,100,90;
(1)、求证: ;(2)、若AB=4,BC=1,求A,C两点旋转所经过的路径长之和.20. 6月26日是“国际禁毒日”某中学组织七、八年级全体学生开展了“禁毒知识”网上竞赛活动,为了解竞赛情况,从两个年级各抽取10名学生的成绩(满分为100分),收集数据为:七年级90,95,95,80,85,90,85,90,85,100;八年级:85,85,95,80,95,90,90,90,100,90;整理数据:

分析数据:
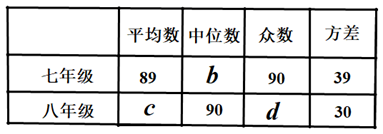
根据以上信息回答下列问题:
(1)、请直接写出表格中 的值(2)、通过数据分析,你认为哪个年级的成绩比较好?说明理由;(3)、该校七八年级共600人,本次竞赛成绩不低于90分的为“优秀”估计这两个年级共多少名学生达到“优秀”?21. 九年级某数学兴趣小组在学习了反比例函数的图象和性质后,进一步研究了函数 的图像与性质,其探究过程如下: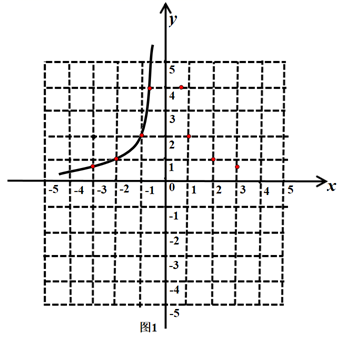
 (1)、绘制函数图象,如图1
(1)、绘制函数图象,如图1①列表;下表是x与y的几组对应值,其中 m= ;

②描点:根据表中各组对应值(x,y)在平面直角坐标系中描出了各点;③连线:用平滑的曲线顺次连接各点,画出了部分图像,请你把图像补充完整;
(2)、通过观察图1,写出该函数的两条性质:①;②;(3)、①观察发现:如图2,若直线y=2交函数 的图像于A,B两点,连接OA,过点B作BC//OA交x轴于点C,则SOABC=;②探究思考:将①的直线y=2改为直线y=a(a>0),其他条件不变,则SOABC=;
③类比猜想:若直线y=a(a>0)交函数 的图像于A,B两点,连接OA,过点B作BC//OA交x轴于C,则 SOABC= ;
22. 如图矩形ABCD中,AB=20,点E是BC上一点,将 沿着AE折叠,点B刚好落在CD边上的点G处,点F在DG上,将 沿着AF折叠,点D刚好落在AG上点H处,此时 . (1)、求证:(2)、求AD的长;(3)、求 的值.23. 为了抗击新冠疫情,我市甲乙两厂积极生产了某种防疫物资共500吨,乙厂的生产量是甲厂的2倍少100吨,这批防疫物资将运往A地240吨,B地260吨,运费如下:(单位:吨)
(1)、求证:(2)、求AD的长;(3)、求 的值.23. 为了抗击新冠疫情,我市甲乙两厂积极生产了某种防疫物资共500吨,乙厂的生产量是甲厂的2倍少100吨,这批防疫物资将运往A地240吨,B地260吨,运费如下:(单位:吨)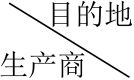
A B 甲 20 25 乙 15 24 (1)、求甲乙两厂各生产了这批防疫多少吨?(2)、设这批物资从乙厂运往A地x吨,全部运往A,B两地的总运费为y元,求y与x之间的函数关系式,并设计使总运费最少的调运方案;(3)、当每吨运费降低m元,( 且m为整数),按(2)中设计的调运方案运输,总运费不超过5200元,求m的最小值.24. 如图1,在平面直角坐标系中, ,以O为圆心,OA的长为半径的半圆O交AO的延长线于C,连接AB,BC,过O作ED//BC分别交AB和半圆O于E,D,连接OB,CD.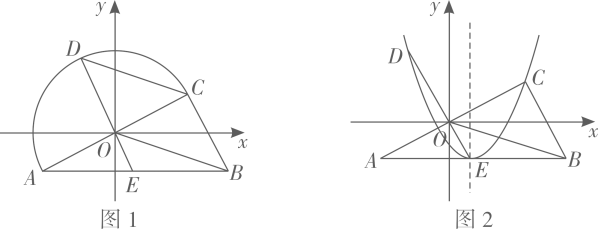 (1)、求证:BC是半圆O的切线;(2)、试判断四边形OBCD的形状,并说明理由;(3)、如图2,若抛物线经过点D,且顶点为E,求此抛物线的解析式;点P 是此抛物线对称轴上的一动点,以E,D,P为顶点的三角形与 相似,问抛物线上是否存在点Q,使得 ,若存在,请直接写出Q点的横坐标;若不存在,说明理由.
(1)、求证:BC是半圆O的切线;(2)、试判断四边形OBCD的形状,并说明理由;(3)、如图2,若抛物线经过点D,且顶点为E,求此抛物线的解析式;点P 是此抛物线对称轴上的一动点,以E,D,P为顶点的三角形与 相似,问抛物线上是否存在点Q,使得 ,若存在,请直接写出Q点的横坐标;若不存在,说明理由.