浙江省温州市泰顺县2020年数学中考二模试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
1. 计算: 的结果是( )A、-7 B、12 C、1 D、-122. 2019年11月11日,天猫双十一开场8分23秒,销售额破40000000000元,比2018年高很多,其中数据40000000000用科学记数法表示为( )A、 B、 C、 D、3. 如图是小强用八块相同的小正方体积木搭建的几何体,这个几何体的主观图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 对泰顺某种学生快餐营养成分进行检测,绘制成如图所示统计图,已知快餐中碳水化合物有120克,那么快餐中脂肪有( )克
4. 对泰顺某种学生快餐营养成分进行检测,绘制成如图所示统计图,已知快餐中碳水化合物有120克,那么快餐中脂肪有( )克 A、300 B、120 C、30 D、1355. 为预防传染病,某校定期对教室进行“药熏消毒”.测出药物燃烧阶段室内每立方米空气中的含药量 和燃烧时间 如下表,根据表中数据,可得每立方米空气中的含药量 关于燃烧时间 的函数表达式为( )
A、300 B、120 C、30 D、1355. 为预防传染病,某校定期对教室进行“药熏消毒”.测出药物燃烧阶段室内每立方米空气中的含药量 和燃烧时间 如下表,根据表中数据,可得每立方米空气中的含药量 关于燃烧时间 的函数表达式为( )燃烧时间
2.5
5
7.5
10
含药量
2
4
6
8
A、 B、 C、 D、6. 某路口交通信号灯的时间设置为:红灯亮25秒,绿灯亮32秒,黄灯亮3秒.当人或车随机经过该路口时,遇到绿灯的概率为( )A、 B、 C、 D、7. 一段圆弧的半径是12,弧长是 ,则这段圆弧所对的圆心角是( )A、 B、 C、 D、8. 某屋顶示意图如图所示,现在屋顶上开一个天窗,天窗 在水平位置,屋顶坡面长度 米,则屋顶水平跨度 的长为( )米. A、 B、 C、 D、9. 已知二次函数 ,当 时,函数y的最大值为4,则m的取值范围是( )A、 B、 C、 D、10. 如图,在正方形 各边上分别截取 ,且 ,若四边形 的面积为 .四边形 面积为 ,当 ,且 时,则 的长为( )
A、 B、 C、 D、9. 已知二次函数 ,当 时,函数y的最大值为4,则m的取值范围是( )A、 B、 C、 D、10. 如图,在正方形 各边上分别截取 ,且 ,若四边形 的面积为 .四边形 面积为 ,当 ,且 时,则 的长为( ) A、 B、3 C、4 D、
A、 B、3 C、4 D、二、填空题
-
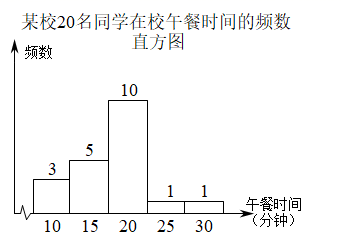
11. 分解因式: .12. 不等式组 的解为.13. 2020年春季复学各校采取年级错时用餐,某校为了了解学生在校午餐所需的时间,抽查了20名同学在校午餐所花的时间,绘制频数直方图如图所示,则可预估该校学生平均用餐时间为分钟.
 14. 如图, 的半径 垂直于弦 ,过点A作 的切线交 的延长线于点P,连结 ,若 ,则 等于度.
14. 如图, 的半径 垂直于弦 ,过点A作 的切线交 的延长线于点P,连结 ,若 ,则 等于度. 15. 如图,菱形 的边 在x轴上,顶点 ,点B在第一象限.将 沿y轴翻折,点D落在x轴上的 处, 交 于点E,且 .若 图象经过点B,则k的值为.
15. 如图,菱形 的边 在x轴上,顶点 ,点B在第一象限.将 沿y轴翻折,点D落在x轴上的 处, 交 于点E,且 .若 图象经过点B,则k的值为. 16. 图1是一种手机托架,使用该手机托架示意图如图3所示,底部放置手机处宽 厘米,托架斜面长 厘米,它有C到F共4个档位调节角度,相邻两个档位间的距离为0.8厘米,档位C到B的距离为2.4厘米.将某型号手机置于托架上(图2),手机屏幕长 是15厘米,O是支点且 厘米(支架的厚度忽略不计).当支架调到E档时,点G离水平面的距离 为厘米;当支架从 档调到F档时,点D离水平面的距离下降了厘米.
16. 图1是一种手机托架,使用该手机托架示意图如图3所示,底部放置手机处宽 厘米,托架斜面长 厘米,它有C到F共4个档位调节角度,相邻两个档位间的距离为0.8厘米,档位C到B的距离为2.4厘米.将某型号手机置于托架上(图2),手机屏幕长 是15厘米,O是支点且 厘米(支架的厚度忽略不计).当支架调到E档时,点G离水平面的距离 为厘米;当支架从 档调到F档时,点D离水平面的距离下降了厘米.
三、解答题
-
17. 计算:(1)、(2)、18. 如图, 平分 , ,且 ,点E在线段 上, 的延长线交 于点F,连接 .
 (1)、求证: .(2)、当 , 时,求 的度数.19. 我国青少年的视力情况已受到全社会的广泛关注,某校随机调研了200名初中七、八、九年级学生的视力情况,并把调查数据绘制成以下统计图:
(1)、求证: .(2)、当 , 时,求 的度数.19. 我国青少年的视力情况已受到全社会的广泛关注,某校随机调研了200名初中七、八、九年级学生的视力情况,并把调查数据绘制成以下统计图: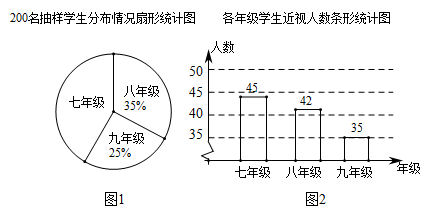 (1)、七年级参加调查的有多少人?若该校有七年级学生500人,请估计七年级的近视人数;(2)、某同学说:“由图2可知,从七年级到九年级近视率越来越低.”你认为这种说法正确吗?请做判断,并说明理由.20. 如图,由32个边长为1的小正三角形组成的网格 中,请按要求画图,且所画格点三角形与格点四边形的顶点均不与点A,B,C,D重合.
(1)、七年级参加调查的有多少人?若该校有七年级学生500人,请估计七年级的近视人数;(2)、某同学说:“由图2可知,从七年级到九年级近视率越来越低.”你认为这种说法正确吗?请做判断,并说明理由.20. 如图,由32个边长为1的小正三角形组成的网格 中,请按要求画图,且所画格点三角形与格点四边形的顶点均不与点A,B,C,D重合.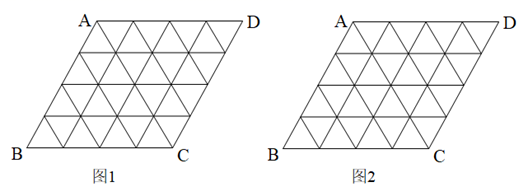 (1)、在图1中画一个格点四边形 ,使点M,N,P,Q分别落在边 , , , 上, 与 互相平分但不相等.(2)、在图2中画一个格点四边形 ,使点M,N,P,Q分别落在边 , , , 上, 与 互相平分且相等.21. 如图,在平面直角坐标系中,抛物线 顶点坐标为 ,图象交x轴正半轴于点A.
(1)、在图1中画一个格点四边形 ,使点M,N,P,Q分别落在边 , , , 上, 与 互相平分但不相等.(2)、在图2中画一个格点四边形 ,使点M,N,P,Q分别落在边 , , , 上, 与 互相平分且相等.21. 如图,在平面直角坐标系中,抛物线 顶点坐标为 ,图象交x轴正半轴于点A. (1)、求二次函数的表达式和点A的坐标.(2)、点 是抛物线上的点,它在对称轴右侧且在第一象限内.将点P向左平移 个单位,将与该二次函数图象上的点Q重合,若 的面积为 ,求n的值.22. 如图,在钝角 中, ,以 为直径作圆O,交 于点D,连结 并延长,交 于点E,连结 .
(1)、求二次函数的表达式和点A的坐标.(2)、点 是抛物线上的点,它在对称轴右侧且在第一象限内.将点P向左平移 个单位,将与该二次函数图象上的点Q重合,若 的面积为 ,求n的值.22. 如图,在钝角 中, ,以 为直径作圆O,交 于点D,连结 并延长,交 于点E,连结 .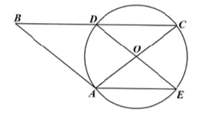 (1)、求证:四边形 是平行四边形。(2)、延长线段 交 于点F,连结 交线段 于点G,若 , 时,求 的直径长.23. “一村一品,绽放致富梦”,泰顺县恩代洋村因猕猴桃被入选全国“一村一品”示范村镇.为更新果树品种,恩代洋村某果农计划购进A、B、C三种果树苗木栽植培育.已知A种果苗每捆比B种果苗每捆多10元,C种果苗每捆30元,购买50捆A种果苗所花钱比购买60捆B种果苗的钱多100元.(每种果苗按整捆购买,且每捆果苗数相同)(1)、A、B种果苗每捆分别需要多少钱;(2)、现批发商推出限时赠送优惠活动:购买一捆A种果苗赠送一捆C种果苗.(最多赠送10捆C种果苗)
(1)、求证:四边形 是平行四边形。(2)、延长线段 交 于点F,连结 交线段 于点G,若 , 时,求 的直径长.23. “一村一品,绽放致富梦”,泰顺县恩代洋村因猕猴桃被入选全国“一村一品”示范村镇.为更新果树品种,恩代洋村某果农计划购进A、B、C三种果树苗木栽植培育.已知A种果苗每捆比B种果苗每捆多10元,C种果苗每捆30元,购买50捆A种果苗所花钱比购买60捆B种果苗的钱多100元.(每种果苗按整捆购买,且每捆果苗数相同)(1)、A、B种果苗每捆分别需要多少钱;(2)、现批发商推出限时赠送优惠活动:购买一捆A种果苗赠送一捆C种果苗.(最多赠送10捆C种果苗)①若购买A种果苗7捆、B种果苗5捆和C种果苗10捆,共需多少钱;
②若需购买C种果苗10捆,预算资金为600元,在不超额的前提下,最多可以买多少捆果苗.求所有满足条件的方案,并指出哪种方案购买费用最少.(每种至少各1捆)
24. 如图,在平面直角坐标系中, 的斜边 在直线 上,且O是 的中点,点A的坐标为 .点 在线段 上从C点向A点运动,同时点Q在线段 上从A点向C点运动,且 .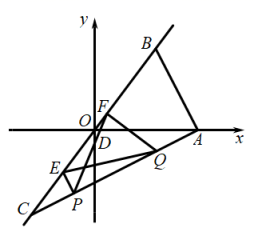 (1)、求 的长及点B的坐标.(2)、作 交 于点E,作 交 于点F,连结 , ,设 .
(1)、求 的长及点B的坐标.(2)、作 交 于点E,作 交 于点F,连结 , ,设 .①在E,F相遇前,用含t的代数式表示 的长.
②当t为何值时, 与坐标轴垂直.
(3)、若 交y轴于点D,除点F与点O重合外, 的值是否为定值,若是,请直接写出 的值,若不是,请直接写出它的取值范围.