浙江省温州市平阳县五校2020年数学中考二模联考试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
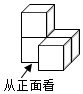
1. 2020的倒数是( )A、-2020 B、2020 C、 D、2. 计算 ,正确的结果是( )A、 B、 C、 D、3. 如图是由4个相同的小正方体组成的一个立体图形,其主视图是( )
 A、
A、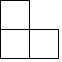 B、
B、 C、
C、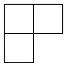 D、
D、 4. 抛物线 的顶点坐标是( )A、 B、 C、 D、5. 不等式组 的解是( )A、 B、 C、 D、6. 已知关于 的一元二次方程 有两个不相等的实数根,则k的值可以是( )A、-2 B、1 C、2 D、37. 挂钟分针的长 ,经过 分钟,它的针尖转过的弧长是( )A、 B、 C、 D、8. 如图,一个小球沿倾斜角为 的斜坡向下滚动,经过5秒时,测得小球的平均速度为 米 秒.已知 ,则小球下降的高度是( )
4. 抛物线 的顶点坐标是( )A、 B、 C、 D、5. 不等式组 的解是( )A、 B、 C、 D、6. 已知关于 的一元二次方程 有两个不相等的实数根,则k的值可以是( )A、-2 B、1 C、2 D、37. 挂钟分针的长 ,经过 分钟,它的针尖转过的弧长是( )A、 B、 C、 D、8. 如图,一个小球沿倾斜角为 的斜坡向下滚动,经过5秒时,测得小球的平均速度为 米 秒.已知 ,则小球下降的高度是( )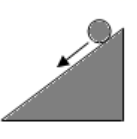 A、1米 B、1.5米 C、2米 D、2.5米9. 二次函数 的部分对应值如下表:
A、1米 B、1.5米 C、2米 D、2.5米9. 二次函数 的部分对应值如下表:x
-2
-1
0
1
2
4
y
5
0
-3
-4
-3
5
则关于x的一元二次方程 的解为( )
A、 , B、 , C、 , D、 ,10. 如图,已知矩形 的周长为 , 和 分别为 和 的内切圆,连接 , , , , ,若 ,则 的长为( )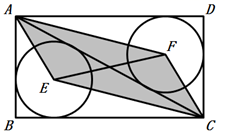 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解: .12. 在一个不透明的袋中,装有3个黄球,2个红球和5个白球,它们除颜色外都相同,从袋中任意摸出一个球,是红球的概率是.13. 在一次体育模拟考试中,某班 个同学的跳绳成绩如下:
178,168,171,170,165,160,167(单位:次 分),
则这组数据的中位数是.
14. 如图,四边形 内接于 ,连接 ,若 ,且 ,则 的度数为. 15. 如图,在平面直角坐标系中,已知菱形 ,点A的坐标为 ,点B,C均在第一象限,反比例函数 的图象经过点C,且与边 交于点D,若D是 的中点,则k的值为.
15. 如图,在平面直角坐标系中,已知菱形 ,点A的坐标为 ,点B,C均在第一象限,反比例函数 的图象经过点C,且与边 交于点D,若D是 的中点,则k的值为.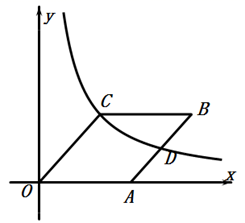 16. 如图1,在 中, , ,D,E分别是边 , 的中点,在边 上取点 ,点G在边 上,且满足 ,连接 ,作 于点 , 于点Q,线段 , , 将 分割成I、II、III、IV四个部分,将这四个部分重新拼接可以得到如图2所示的矩形 ,若 ,则图1中 的长为.
16. 如图1,在 中, , ,D,E分别是边 , 的中点,在边 上取点 ,点G在边 上,且满足 ,连接 ,作 于点 , 于点Q,线段 , , 将 分割成I、II、III、IV四个部分,将这四个部分重新拼接可以得到如图2所示的矩形 ,若 ,则图1中 的长为.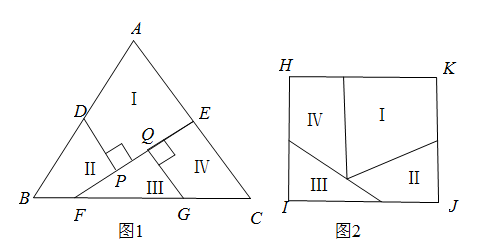
三、解答题
-
17.(1)、计算:(2)、解方程:18. 如图,在正方形 中,E是 边上的点,连接 ,作 于点O,且点F在 边上.
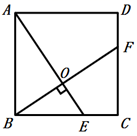 (1)、求证: .(2)、若 , ,求 的长.19. 某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项素质测试.他们的各项测试成绩如下表所示:
(1)、求证: .(2)、若 , ,求 的长.19. 某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项素质测试.他们的各项测试成绩如下表所示:创新能力
综合知识
语言能力
A
72
50
88
B
85
74
45
C
68
70
67
(1)、根据三项测试的平均成绩,从高到低确定三名应聘者的排名顺序.(2)、根据实际需要,公司将创新能力、综合知识和语言能力三项测试得分按 的比例确定三人的测试成绩,请你说明谁将被录用.20. 如图,抛物线 与x轴的正半轴交于点A,其顶点为M,点P在该抛物线上且位于A、M两点之间,过点P作 轴于点B, 轴于点C, 与抛物线的另一交点为D,连接 .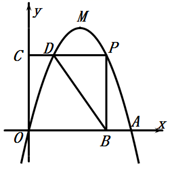 (1)、求该抛物线的对称轴及点A的坐标.(2)、当点P关于 的对称点恰好落在x轴上时,求点P的坐标.21. 如图,在 的正方形格中,已知 的顶点B,C均在格点上,顶点A在小正方形的边上(不在格点),要求仅用一把无刻度的直尺,且不能用直尺中的直角完成下列作图.
(1)、求该抛物线的对称轴及点A的坐标.(2)、当点P关于 的对称点恰好落在x轴上时,求点P的坐标.21. 如图,在 的正方形格中,已知 的顶点B,C均在格点上,顶点A在小正方形的边上(不在格点),要求仅用一把无刻度的直尺,且不能用直尺中的直角完成下列作图.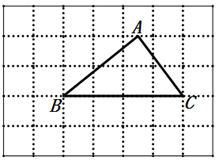 (1)、在图甲中作 的边 上的高线 .(2)、在图乙中过点A作一直线,使它将 的面积分成 的两部分.
(1)、在图甲中作 的边 上的高线 .(2)、在图乙中过点A作一直线,使它将 的面积分成 的两部分.(说明:图甲和图乙在答卷纸上.)
22. 如图,已知在 中, ,点O在边 上,以 为半径的 与 边切于点D, 与 , 边的另一交点分别为E,F.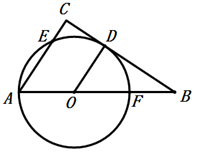 (1)、求证: .(2)、若 , ,求 的半径.23. 榴莲上市的时候,某水果行以“线上”与“线下”相结合的方式一共销售了100箱榴莲.已知“线上”销售的每箱利润为100元.“线下”销售的每箱利润y(元)与销售量x(箱) 之间的函数关系如图中的线段 .
(1)、求证: .(2)、若 , ,求 的半径.23. 榴莲上市的时候,某水果行以“线上”与“线下”相结合的方式一共销售了100箱榴莲.已知“线上”销售的每箱利润为100元.“线下”销售的每箱利润y(元)与销售量x(箱) 之间的函数关系如图中的线段 .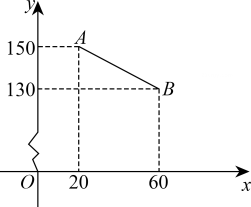 (1)、求y与x之间的函数关系.(2)、当“线下”的销售利润为4350元时,求x的值.(3)、实际“线下”销售时,每箱还要支出其它费用a元 ,若“线上”与“线下”售完这100箱榴莲所获得的最大总利润为11250元,求a的值.24. 如图,在矩形 中, ,点E是边 的中点, 和 的延长线交于点F,点G是边 上的一点,且满足 ,连接 , ,且 与 交于点O.
(1)、求y与x之间的函数关系.(2)、当“线下”的销售利润为4350元时,求x的值.(3)、实际“线下”销售时,每箱还要支出其它费用a元 ,若“线上”与“线下”售完这100箱榴莲所获得的最大总利润为11250元,求a的值.24. 如图,在矩形 中, ,点E是边 的中点, 和 的延长线交于点F,点G是边 上的一点,且满足 ,连接 , ,且 与 交于点O.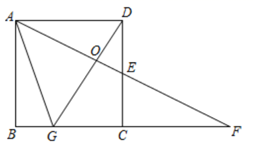 (1)、若 ,求 的面积(2)、当 是直角三角形时,求所有满足要求的a值.(3)、记 , ,
(1)、若 ,求 的面积(2)、当 是直角三角形时,求所有满足要求的a值.(3)、记 , ,①求y关于x的函数关系.
②当 时,求 的值.