浙江省湖州市2020年数学中考最后一模试卷（6月）
试卷更新日期：2020-08-10 类型：中考模拟
一、选择题
-
1. 19的相反数是（ ）A、﹣19 B、- C、 D、192. 截至5月6日，Covid﹣19感染人数己超365万，将365万用科学记数法表示为（ ）A、365×104 B、3.65×105 C、3.65×106 D、3.65×1073. 计算 的结果是（ ）A、 B、 C、 D、14. 如图，点D在△ABC的边AB的延长线上，DE∥BC，若∠A＝32°，∠C＝26°，则∠D的度数是（ ）
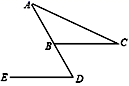A、58° B、59° C、60° D、69°5. 如图，扇形纸扇完全打开后，外侧两竹条AB，AC夹角为150°，AB的长为32cm，BD的长为14cm，则 的长为（ ）cm．
A、 π B、12π C、15π D、36π6. 疫情防控，我们一直在坚守.某居委会组织两个检查组，分别对“居民体温”和“居民安全出行”的情况进行抽查.若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查，则他们恰好抽到同一个小区的概率是（ ）A、 B、 C、 D、7. 如图，在正六边形ABCDEF外作正方形DEGH，连接AH，则tan∠HAB等于（ ）
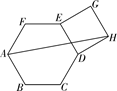A、3 B、 C、2 D、8. 如图，正方形ABCD的面积为144，菱形BCEF面积为108，则△ABF面积为（ ）
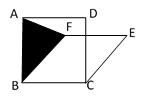A、18 B、36 C、18 D、369. 三角形纸片ABC中，∠C＝90°，甲折叠纸片使点A与点B重合，压平得到的折痕长记为m；乙折叠纸片使得CA与CB所在的直线重合，压平得到的折痕长记为n，则m，n的大小关系是（ ）A、m≤n B、m＜n C、m≥n D、m＞n10. 四位同学在研究函数 （ 是常数）时，甲发现当 时，函数有最小值；乙发现 是方程 的一个根；丙发现函数的最小值为3；丁发现当 时， ，已知这四位同学中只有一位发现的结论是错误的，则该同学是（ ）A、甲 B、乙 C、丙 D、丁二、填空题
-
11. 分解因式： ．12. 如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连结BC.若∠A＝36°，则∠C=.
13. 自从“新冠病毒”爆发以来，胖胖同学每周且每天3次自测体温，结果统计如下表：则这些体温的众数是℃.体温（℃）
36.1
36.2
36.3
36.4
36.5
36.6
36.7
次数
2
3
4
6
3
1
2
14. 如图，是将一正方体货物沿坡面AB装进汽车货厢的平面示意图，已知长方体货厢的高度BC为2.6米，斜坡AB的坡比为1：2.4，现把图中的货物继续向前平移，当货物顶点D与C重合时，仍可把货物放平装进货厢，则货物的高度BD不能超过米.
15. 如图，直线l与反比例函数y＝ （k≠0）的图象在第二象限交于B、C两点，与x轴交于点A，连接OC，∠ACO的角平分线交x轴于点D．若AB：BC：CO＝1：2：2，△COD的面积为6，则k的值为 ．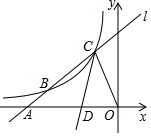
16. 如图是一个边长为 的正方形，它是由①②③④四个完全相同的三角形和图⑤边长为 的正方形无缝隙拼成.若这个图形不用剪裁，可以无缝隙拼成长方形，则 应满足关系式 ．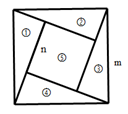
三、解答题
-
17. 计算（－3）2+20200－ .18. 计算： .19. 如图，一次函数y=kx+b的图象与x轴交于点B（6，0），与y轴交于点A，与二次函数y=ax2的图象在第一象限内交于点C（3，3）.
(1)、求此一次函数与二次函数的表达式；(2)、若点D在线段AC上，与y轴平行的直线DE与二次函数图象相交于点E，∠ADO=∠OED，求点D坐标.20. 今年猪肉价格受非洲猪瘟疫情影响，有较大幅度的上升，为了解某地区养殖户受非洲猪瘟疫情感染受灾情况，现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查（把调查结果分为四个等级：A级：非常严重；B级：严重；C级：一般；D级：没有感染），并将调查结果绘制成如下两幅不完整的统计图．请根据统计图中的信息解决下列问题：
(1)、本次抽样调查的养殖户的总户数是；把图2条形统计图补充完整．(2)、若该地区建档的养殖户有1500户，求非常严重与严重的养殖户一共有多少户？(3)、某调研单位想从5户建档养殖户（分别记为a，b，c，d，e）中随机选取两户，进一步跟踪监测病毒传播情况，请用列表或画树状图的方法求出选中养殖户e的概率．21. 如图，已知矩形 ，对角线 的垂直平分线分别交 ， 和 于点 ， ， ． ， 的延长线交于点 ，且 ，连接 ．
(1)、求证：(2)、求证： 平分 ．22. A，B两城相距600千米，甲、乙两车同时从A城出发驶向B城，甲车到达B城后立即返回.如图是它们离A城的距离y（千米）与行驶时间 x（小时）之间的函数图象.
(1)、求甲车行驶过程中y与x之间的函数解析式，并写出自变量x的取值范围；(2)、当它们行驶了7小时时，两车相遇，求乙车的速度及乙车行驶过程中y与x之间的函数解析式，并写出自变量x的取值范围；(3)、当两车相距100千米时，求甲车行驶的时间.23. 如图，⊙A过▱OBCD的三顶点O、D、C，边OB与⊙A相切于点O，边BC与⊙O相交于点H，射线OA交边CD于点E，交⊙A于点F，点P在射线OA上，且∠PCD=2∠DOF，以O为原点，OP所在的直线为x轴建立平面直角坐标系，点B的坐标为（0，﹣2）．
(1)、若∠BOH=30°，求点H的坐标；(2)、求证：直线PC是⊙A的切线；(3)、若OD= ，求⊙A的半径．24. 如图，在直角坐标系中，长方形ABCD（每个内角都是90°）的顶点的坐标分别是A（0，m），B（n，0），（m＞n＞0），点E在AD上，AE＝AB，点F在y轴上，OF＝OB，BF的延长线与DA的延长线交于点M，EF与AB交于点N.
(1)、试求点E的坐标（用含m，n的式子表示）；(2)、求证：AM＝AN；(3)、若AB＝CD＝12cm，BC＝20cm，动点P从B出发，以2cm/s的速度沿BC向C运动的同时，动点Q从C出发，以vcm/s的速度沿CD向D运动，是否存在这样的v值，使得△ABP与△PQC全等？若存在，请求出v值；若不存在，请说明理由.