浙江省杭州市2020年数学中考最后一模试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
1. 计算: 的结果是( )A、1 B、 C、0 D、-12. 二十四节气是中国古代劳动人民长期经验积累的结品,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长.下图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长超过14小时的节气是( )
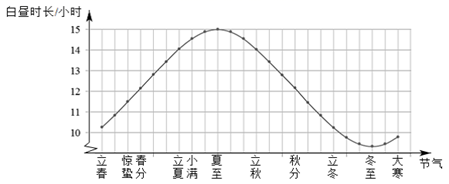 A、惊蛰 B、立夏 C、夏至 D、大寒3. 如图,在 中, , ,以BC的中点O为圆心的 分别与AB,AC相切于D,E两点,则 的长为( )
A、惊蛰 B、立夏 C、夏至 D、大寒3. 如图,在 中, , ,以BC的中点O为圆心的 分别与AB,AC相切于D,E两点,则 的长为( )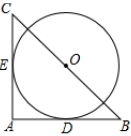 A、 B、 C、 D、4. 肆虐的冠状病毒肺炎具有人传人性,调查发现:1人感染病毒后如果不隔离,那么经过两轮传染将会有225人感染,若设1人平均感染x人,依题意可列方程( )A、1+x=225 B、1+x2=225 C、(1+x)2=225 D、1+(1+x2 )=2255. 如图,截止5月1日浙江抗击新冠肺炎部分城市治愈总人数统计表,下列说法错误的是( )
A、 B、 C、 D、4. 肆虐的冠状病毒肺炎具有人传人性,调查发现:1人感染病毒后如果不隔离,那么经过两轮传染将会有225人感染,若设1人平均感染x人,依题意可列方程( )A、1+x=225 B、1+x2=225 C、(1+x)2=225 D、1+(1+x2 )=2255. 如图,截止5月1日浙江抗击新冠肺炎部分城市治愈总人数统计表,下列说法错误的是( )城市
杭州
宁波
金华
温州
台州
治愈总人数
181
157
55
503
146
A、金华治愈总人数最少 B、杭州治愈总人数最多 C、温州治愈总人数503人 D、宁波治愈总人数比台州多6. 如图,点G、F分别是△ACD的边AC、CD上的点,AD的延长线与GF的延长线相交于点B,DE∥AC交GB于点E,则下列结论错误的是( )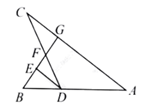 A、 B、 C、 D、7. 下列命题中假命题是( )A、正六边形的外角和等于360° B、位似图形必定相似 C、对角线相等的四边形是矩形 D、两组对角相等的四边形是平行四边形8. 如图所示,在平面直角坐标系中,直线y1=2x+4分别与x轴,y轴交于A,B两点,以线段OB为一条边向右侧作矩形OCDB,且点D在直线y2=﹣x+b上,若矩形OCDB的面积为20,直线y1=2x+4与直线y2=﹣x+b交于点P.则P的坐标为( )
A、 B、 C、 D、7. 下列命题中假命题是( )A、正六边形的外角和等于360° B、位似图形必定相似 C、对角线相等的四边形是矩形 D、两组对角相等的四边形是平行四边形8. 如图所示,在平面直角坐标系中,直线y1=2x+4分别与x轴,y轴交于A,B两点,以线段OB为一条边向右侧作矩形OCDB,且点D在直线y2=﹣x+b上,若矩形OCDB的面积为20,直线y1=2x+4与直线y2=﹣x+b交于点P.则P的坐标为( ) A、(2,8) B、 C、 D、(4,12)9. 如图,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻两树CD之间的距离为50米,某人在河岸MN的A处测得∠DAN=45°,然后沿河岸走了130米到达B处,测得∠CBN=60°.则河流的宽度CE为( )
A、(2,8) B、 C、 D、(4,12)9. 如图,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻两树CD之间的距离为50米,某人在河岸MN的A处测得∠DAN=45°,然后沿河岸走了130米到达B处,测得∠CBN=60°.则河流的宽度CE为( ) A、80 B、40(3﹣ ) C、40(3+ ) D、4010. 抛物线 与 轴的公共点是 , ,直线 经过点 ,直线 与抛物线 另一个交点的横坐标是4,它们的图象如图所示,有以下结论:
A、80 B、40(3﹣ ) C、40(3+ ) D、4010. 抛物线 与 轴的公共点是 , ,直线 经过点 ,直线 与抛物线 另一个交点的横坐标是4,它们的图象如图所示,有以下结论:①拋物线对称轴是 ;
② ;
③ 时, ;
④若 ,则 .
其中正确的个数为( )
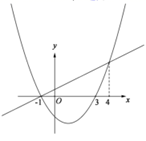 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 分解因式: .12. 在本学期的五次数学检测中,甲同学的成绩是: ,乙同学的成绩是: ,两名同学成绩比较稳定的是 (填“甲”或“乙”) .13. 如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为 ,则图中阴影部分的面积为.
 14. 如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为.
14. 如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为. 15. 如图,已知点M的坐标为(4,3),点 M 关于直线 l:y=﹣x+b 的对称点落在坐标轴上,则 b的值为 .
15. 如图,已知点M的坐标为(4,3),点 M 关于直线 l:y=﹣x+b 的对称点落在坐标轴上,则 b的值为 . 16. 如图,矩形ABCD中,AB=4,AD=8,点E为AD上一点,将△ABE沿BE折叠得到△FBE , 点G为CD上一点,将△DEG沿EG折叠得到△HEG , 且E、F、H三点共线,当△CGH为直角三角形时,AE的长为
16. 如图,矩形ABCD中,AB=4,AD=8,点E为AD上一点,将△ABE沿BE折叠得到△FBE , 点G为CD上一点,将△DEG沿EG折叠得到△HEG , 且E、F、H三点共线,当△CGH为直角三角形时,AE的长为
三、解答题
-
17. 化简:18. 为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看 次的人数没有标出).
根据上述信息,解答下列各题:
 ×(1)、该班级女生人数是 , 女生收看“两会”新闻次数的中位数是;(2)、对于某个群体,我们把一周内收看某热点新闻次数不低于 次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低 ,试求该班级男生人数;(3)、为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
×(1)、该班级女生人数是 , 女生收看“两会”新闻次数的中位数是;(2)、对于某个群体,我们把一周内收看某热点新闻次数不低于 次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低 ,试求该班级男生人数;(3)、为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).统计量
平均数(次)
中位数(次)
众数(次)
方差
…
该班级男生
…
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
19. 如图,在矩形 中,小聪同学利用直尺和圆规完成了如下操作: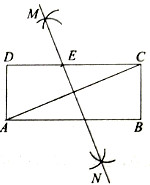
①分别以点 和 为圆心,以大于 的长为半径作弧,两弧相交于点 和 ;
②作直线 ,交 于点 .
请你观察图形解答下列问题:
(1)、 与 的位置关系:直线 是线段 的线;
(2)、若 , ,求矩形的对角线 的长.20. 在平面直角坐标系 中,A(-4,3),B(0,1),将线段AB沿 轴的正方向平移 个单位,得到线段A′B′,且A′,B′恰好都落在反比例函数 的图象上.(1)、用含 的代数式表示点A′,B′的坐标;(2)、求 的值和反比例函数 的表达式;(3)、点 为反比例函数 图象上的一个动点,直线 与 轴交于点 ,若 ,请直接写出点C的坐标.21. 如图,在▱ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于 点F,连接BE,∠F=45°. (1)、求证:四边形ABCD是矩形;(2)、若AB=14,DE=8,求sin∠AEB的值.22. 在平面直角坐标系 中,抛物线 与 轴交于A,B两点(点A在点B左侧)(1)、求抛物线的顶点坐标(用含 的代数式表示);(2)、求线段AB的长;(3)、抛物线与 轴交于点C(点C不与原点 重合),若 的面积始终小于 的面积,求 的取值范围.23. 如图,在 中, , , ,以点 为圆心,以 为半径作优弧 ,交 于点 ,交 于点 .点 在优弧 上从点 开始移动,到达点 时停止,连接 .
(1)、求证:四边形ABCD是矩形;(2)、若AB=14,DE=8,求sin∠AEB的值.22. 在平面直角坐标系 中,抛物线 与 轴交于A,B两点(点A在点B左侧)(1)、求抛物线的顶点坐标(用含 的代数式表示);(2)、求线段AB的长;(3)、抛物线与 轴交于点C(点C不与原点 重合),若 的面积始终小于 的面积,求 的取值范围.23. 如图,在 中, , , ,以点 为圆心,以 为半径作优弧 ,交 于点 ,交 于点 .点 在优弧 上从点 开始移动,到达点 时停止,连接 .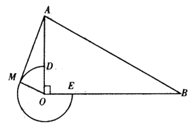

备用图
(1)、当 时,判断 与优弧 的位置关系,并加以证明;(2)、当 时,求点 在优弧 上移动的路线长及线段 的长.(3)、连接 ,设 的面积为 ,直接写出 的取值范围.