辽宁省营口市2020年数学中考三模试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
1. 的相反数是( )A、2020 B、-2020 C、 D、2. 下列运算错误的是( )A、a+2a=3a B、(a2)3=a6 C、a2•a3=a5 D、a6÷a3=a23. 下列图形中是轴对称图形但不是中心对称图形的是( )A、
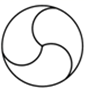 B、
B、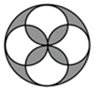 C、
C、 D、
D、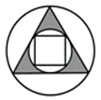 4. 下列调查中,最适合采用全面调查(普查)的是( )A、对我市中学生每周课外阅读时间情况的调查 B、对我市市民知晓“礼让行人”交通新规情况的调查 C、对我市中学生观看春节免费电影《囧妈》情况调查 D、对“新型冠状病毒”期间某航班内全体乘客人员体温情况的调查5. 如图,在 中, ,分别以B,C为圆心,大于BC的一半为半径作弧,两弧相交于D,E,作直线DE交AB,BC于点F,G,连接CF,若 ,则 的长为( )
4. 下列调查中,最适合采用全面调查(普查)的是( )A、对我市中学生每周课外阅读时间情况的调查 B、对我市市民知晓“礼让行人”交通新规情况的调查 C、对我市中学生观看春节免费电影《囧妈》情况调查 D、对“新型冠状病毒”期间某航班内全体乘客人员体温情况的调查5. 如图,在 中, ,分别以B,C为圆心,大于BC的一半为半径作弧,两弧相交于D,E,作直线DE交AB,BC于点F,G,连接CF,若 ,则 的长为( )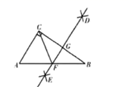 A、3.5 B、3 C、2.5 D、26. 如图,过⊙O外一点P引⊙O的两条切线PA,PB,切点分别是A,B,OP交⊙O于点C,点D是 上不与点A、点C重合的一个动点,连接AD,CD,若∠APB=80°,则∠ADC的度数是( )
A、3.5 B、3 C、2.5 D、26. 如图,过⊙O外一点P引⊙O的两条切线PA,PB,切点分别是A,B,OP交⊙O于点C,点D是 上不与点A、点C重合的一个动点,连接AD,CD,若∠APB=80°,则∠ADC的度数是( )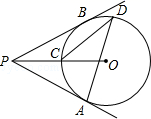 A、15° B、20° C、25° D、30°7. 如图,△OAC和△BAD都是等腰直角三角形, ,反比例函数 在第一象限的图象经过点B,则S△OAC-S△BAD=( )
A、15° B、20° C、25° D、30°7. 如图,△OAC和△BAD都是等腰直角三角形, ,反比例函数 在第一象限的图象经过点B,则S△OAC-S△BAD=( )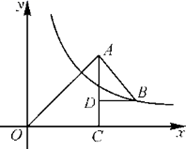 A、1.5 B、2.5 C、3 D、18. 新型冠状肺炎疫情正在全球蔓延肆虐,口罩成了人们生活中必不可少的物品,某口罩厂有26名工人,每人每天可以生产800个口罩面或1000个口罩耳绳.一个口罩面需要配两个耳绳,为使每天生产的口罩刚好配套,设安排x名工人生产口罩面,则下面所列方程正确的是( )A、2×1000(26﹣x)=800x B、1000(13﹣x)=800x C、1000(26﹣x)=2×800x D、1000(26﹣x)=800x9. 如图,在 中,点 分别在 边上,连接 ,若 ,则下列结论错误的是( )
A、1.5 B、2.5 C、3 D、18. 新型冠状肺炎疫情正在全球蔓延肆虐,口罩成了人们生活中必不可少的物品,某口罩厂有26名工人,每人每天可以生产800个口罩面或1000个口罩耳绳.一个口罩面需要配两个耳绳,为使每天生产的口罩刚好配套,设安排x名工人生产口罩面,则下面所列方程正确的是( )A、2×1000(26﹣x)=800x B、1000(13﹣x)=800x C、1000(26﹣x)=2×800x D、1000(26﹣x)=800x9. 如图,在 中,点 分别在 边上,连接 ,若 ,则下列结论错误的是( ) A、 B、 C、 D、10.
A、 B、 C、 D、10.如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
 A、
A、 B、
B、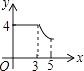 C、
C、 D、
D、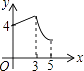
二、填空题
-
11. 在函数y= 中,自变量x的取值范围是.12. 改革开放以来,中国经济总量不断创新高,在2019年中国经济总量达到99.0865万亿元,将数99.0865万亿元用科学记数法表示为 元.13. 分解因式: .14. 小华为参加毕业晚会演出,准备制一顶圆锥形彩色纸帽,如图所示,如果纸帽的底面半径为8cm,母线长为25cm,那么制作这顶纸帽至少需要彩色纸板的面积为cm2.(结果保留π)
 15. 在防治新型冠状病毒知识问答中,10名参赛选手得分情况如下表:那么这10名选手所得分数的中位数.
15. 在防治新型冠状病毒知识问答中,10名参赛选手得分情况如下表:那么这10名选手所得分数的中位数.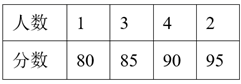 16. 如图,△ABC内接于⊙O,∠C=45°,AB=6,则⊙O的半径为 .
16. 如图,△ABC内接于⊙O,∠C=45°,AB=6,则⊙O的半径为 . 17. 如图,矩形ABCD中,AB=12,AD=15,E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处,点P是线段CB延长线上的动点,连接PA,若△PAF是等腰三角形,则PB的长为.
17. 如图,矩形ABCD中,AB=12,AD=15,E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处,点P是线段CB延长线上的动点,连接PA,若△PAF是等腰三角形,则PB的长为. 18. 二次函数y= x2的图象如图,点A0位于坐标原点,点A1 , A2 , A3…An在y轴的正半轴上,点B1 , B2 , B3…Bn在二次函数位于第一象限的图象上,点C1 , C2 , C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1 , 四边形A1B2A2C2 , 四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形A2019B2020A2020C2020的周长为 .
18. 二次函数y= x2的图象如图,点A0位于坐标原点,点A1 , A2 , A3…An在y轴的正半轴上,点B1 , B2 , B3…Bn在二次函数位于第一象限的图象上,点C1 , C2 , C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1 , 四边形A1B2A2C2 , 四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形A2019B2020A2020C2020的周长为 .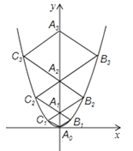
三、解答题
-
19. 化简分式:( ﹣ )÷ 并从﹣2,0,1,2这四个数中选取一个合适的数作a的值代入求值.20. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到A小区的概率是多少(2)、请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.21. 2019年全国两会于3月5日在人民大会堂开幕,某社区为了解居民对此次两会的关注程度,在全社区范围内随机抽取部分居民进行问卷调查,根据调查结果,把居民对两会的关注程度分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下不完整的统计图:

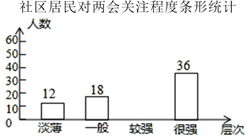
请结合图表中的信息,解答下列问题:
(1)、此次调查一共随机抽取了名居民;(2)、请将条形统计图补充完整;(3)、扇形统计图中,“很强”所对应扇形圆心角的度数为;(4)、若该社区有1500人,则可以估计该社区居民对两会的关注程度为“淡薄”层次的约有 人.22. 如图,某高楼顶部有一信号发射塔,在矩形建筑物 的 两点测得该塔顶端 的仰角分别为 和 ,矩形建筑物的宽度 ,高度 ,求信号发射塔顶端到地面的距离 . (结果精确到 )(参考数据: )
 23. 已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连接AE,交CD于点F.
23. 已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连接AE,交CD于点F.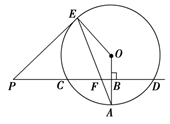 (1)、若⊙O的半径为8,求CD的长;(2)、若PF=13,求PE的长;(3)、在(2)的条件下,sinA= ,求EF的长.24. 某公司展销如图所示的长方形工艺品,该工艺品长60cm宽40cm,中间镶有宽度相同的三条丝绸花边.
(1)、若⊙O的半径为8,求CD的长;(2)、若PF=13,求PE的长;(3)、在(2)的条件下,sinA= ,求EF的长.24. 某公司展销如图所示的长方形工艺品,该工艺品长60cm宽40cm,中间镶有宽度相同的三条丝绸花边.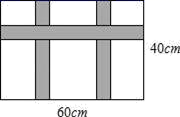 (1)、若丝绸花边的面积(阴影面积)为650cm2 , 求丝绸花边的宽度;(2)、已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天还需支付各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件.
(1)、若丝绸花边的面积(阴影面积)为650cm2 , 求丝绸花边的宽度;(2)、已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天还需支付各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件.(ⅰ)若想每天获利18000元,该公司应该把销售单价定为多少元?
(ⅱ)该公司应该把销售单价定为多少元,才能使每天所获销售利润最大?最大利润是多少?
25. 如图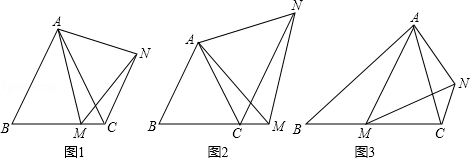
(提出问题)
(1)、如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.(2)、如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.(3)、如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.26. 如图,已知抛物线y=x2+bx+c与x轴交于A、B两点,交y轴于点C,AB=4,对称轴是直线x=﹣1.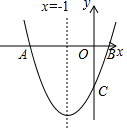 (1)、求抛物线的解析式及点C的坐标;(2)、连接AC,E是线段OC上一点,点E关于直线x=﹣1的对称点F正好落在AC上,求点F的坐标;(3)、动点M从点O出发,以每秒2个单位长度的速度向点A运动,到达点A即停止运动,过点M作x轴的垂线交抛物线于点N,交线段AC于点Q.设运动时间为t(t>0)秒.
(1)、求抛物线的解析式及点C的坐标;(2)、连接AC,E是线段OC上一点,点E关于直线x=﹣1的对称点F正好落在AC上,求点F的坐标;(3)、动点M从点O出发,以每秒2个单位长度的速度向点A运动,到达点A即停止运动,过点M作x轴的垂线交抛物线于点N,交线段AC于点Q.设运动时间为t(t>0)秒.①连接BC,若△BOC与△AMN相似,请直接写出t的值;
②△AOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.