辽宁省五城市2020年数学中考一模试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
1. 的绝对值是( )A、 B、 C、-2020 D、20202. 下列计算结果正确的是( )A、 B、 C、 D、3. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列对一元二次方程x2+x﹣3=0根的情况的判断,正确的是( )A、有两个不相等实数根 B、有两个相等实数根 C、有且只有一个实数根 D、没有实数根5. 顺次连结任意四边形各边中点所得到的四边形一定是( )A、平行四边形 B、菱形 C、矩形 D、正方形6. 为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
4. 下列对一元二次方程x2+x﹣3=0根的情况的判断,正确的是( )A、有两个不相等实数根 B、有两个相等实数根 C、有且只有一个实数根 D、没有实数根5. 顺次连结任意四边形各边中点所得到的四边形一定是( )A、平行四边形 B、菱形 C、矩形 D、正方形6. 为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:捐款的数额(单位:元)
5
10
20
50
100
人数(单位:个)
2
4
5
3
1
关于这15名同学所捐款的数额,下列说法正确的是( )
A、众数是100 B、平均数是30 C、极差是20 D、中位数是207. 如图, 中, , , ,则 的长为( )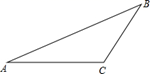 A、 B、 C、5 D、8. 如图,矩形 中,E是 的中点,且 ,当 时, 等于( )
A、 B、 C、5 D、8. 如图,矩形 中,E是 的中点,且 ,当 时, 等于( ) A、 B、 C、 D、9. 如图,在 中, ,以 为直径的 分别交 、 于点D、E,点F在 的延长线上,且 , ,则 的长为( )
A、 B、 C、 D、9. 如图,在 中, ,以 为直径的 分别交 、 于点D、E,点F在 的延长线上,且 , ,则 的长为( )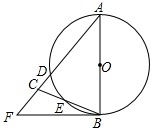 A、 B、 C、 D、10. 如图是二次函数 的图象,下列结论:
A、 B、 C、 D、10. 如图是二次函数 的图象,下列结论:①二次三项式 的最大值为4;② ;③一元二次方程 的两根之和为 ;④使 成立的 的取值范围是 ;⑤抛物线上有两点 和 ,若 ,且 ,则
其中正确的个数有( ).
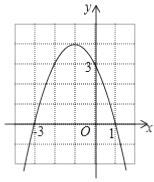 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
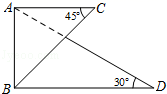
11. 华为 系列是近期相当火爆的 国产手机,它采用的麒麟990 芯片在指甲盖大小的尺寸上集成了103亿个晶体管,将103亿用科学记数法表示为.12. 因式分解: .13. 等腰三角形的一边长为2,周长为5,那么它的腰长为.14. 正六边形的外接圆的半径与内切圆的半径之比为.15. 如图,将一副三角板按图中方式叠放,BC=4,那么BD=
 16. 如图,在地板的环形图案上, ,任意抛出一个乒乓球,落在阴影区域的概率是.
16. 如图,在地板的环形图案上, ,任意抛出一个乒乓球,落在阴影区域的概率是.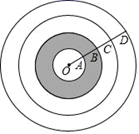 17. 如图,过点C(3,4)的直线 交 轴于点A,∠ABC=90°,AB=CB,曲线 过点B,将点A沿 轴正方向平移 个单位长度恰好落在该曲线上,则 的值为.
17. 如图,过点C(3,4)的直线 交 轴于点A,∠ABC=90°,AB=CB,曲线 过点B,将点A沿 轴正方向平移 个单位长度恰好落在该曲线上,则 的值为.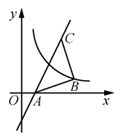 18. 如图,在平面直角坐标系中, ,以 为一边,在第一象限作菱形 ,并使 ,再以对角线 为一边,在如图所示的一侧作相同形状的菱形 ,再依次作菱形 , ,……, ,则 的长度为.
18. 如图,在平面直角坐标系中, ,以 为一边,在第一象限作菱形 ,并使 ,再以对角线 为一边,在如图所示的一侧作相同形状的菱形 ,再依次作菱形 , ,……, ,则 的长度为.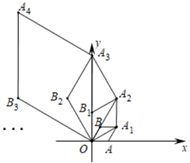
三、解答题
-
19. 先化简,再求值: ,其中 .20. △ABC在边长为l的正方形网格中如图所示.
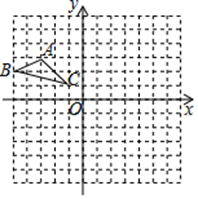 (1)、①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2.且△A1B1C位于点C的异侧,并表示出A1的坐标.
(1)、①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2.且△A1B1C位于点C的异侧,并表示出A1的坐标.
②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.(2)、在(2)的条件下求出点B经过的路径长.21. 为了解某校九年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行统计,结果如下表,并绘制了如下尚不完整的统计图,已知B,E两组发言的人数比为5:2,请结合图表中相关数据回答下列问题: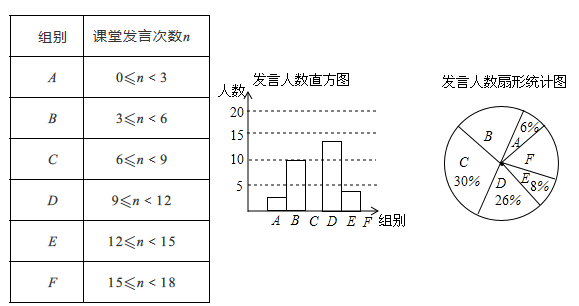 (1)、本次抽样的学生人数为;(2)、补全条形统计图;(3)、该年级共有学生500人,请估计这天全年级发言次数不少于12的人数;(4)、已知 组发言的学生中有1位女生, 组发言的学生中有2位男生,现从 组与 组中分别抽一位学生写报告,请用树状图或列表法,求所抽到的两位学生恰好是一男一女的概率.22. 如图,已知∠AOB=90°,∠OAB=30°,反比例函数 的图象过点 ,反比例函数 的图象过点A.
(1)、本次抽样的学生人数为;(2)、补全条形统计图;(3)、该年级共有学生500人,请估计这天全年级发言次数不少于12的人数;(4)、已知 组发言的学生中有1位女生, 组发言的学生中有2位男生,现从 组与 组中分别抽一位学生写报告,请用树状图或列表法,求所抽到的两位学生恰好是一男一女的概率.22. 如图,已知∠AOB=90°,∠OAB=30°,反比例函数 的图象过点 ,反比例函数 的图象过点A.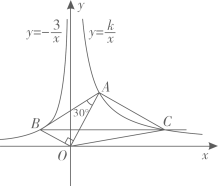 (1)、求 和 的值.(2)、过点B作BC∥x轴,与双曲线 交于点C.求△OAC的面积.23. 如图, 是 的直径,点P是 延长线上一点,过点P作 的切线 ,切点是C,过点C作弦 于E,连接 , .
(1)、求 和 的值.(2)、过点B作BC∥x轴,与双曲线 交于点C.求△OAC的面积.23. 如图, 是 的直径,点P是 延长线上一点,过点P作 的切线 ,切点是C,过点C作弦 于E,连接 , .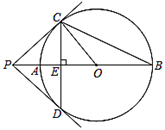 (1)、求证: 是 的切线;(2)、若 , ,求 的长.24. 鄂尔多斯市某百货商场销售某一热销商品A,其进货和销售情况如下:用16000元购进一批该热销商品A,上市后很快销售一空,根据市场需求情况,该商场又用7500元购进第二批该商品,已知第二批所购件数是第一批所购件数的一半,且每件商品的进价比第一批的进价少10元.(1)、求商场第二批商品A的进价;(2)、商场同时销售另一种热销商品B,已知商品B的进价与第二批商品A的进价相同,且最初销售价为165元,每天能卖出125件,经市场销售发现,若售价每上涨1元,其每天销售量就减少5件,问商场该如何定售价,每天才能获得最大利润?并求出每天的最大利润是多少?25. 在 中, , ,点E是直线 上一动点,点D是直线 上动点,点F是直线 上一动点,且 , .(1)、如图1,当点D,E,F分别在 , , 边上时,请你判断线段 , , 之间有怎样的数量关系?请直接写出你的结论;
(1)、求证: 是 的切线;(2)、若 , ,求 的长.24. 鄂尔多斯市某百货商场销售某一热销商品A,其进货和销售情况如下:用16000元购进一批该热销商品A,上市后很快销售一空,根据市场需求情况,该商场又用7500元购进第二批该商品,已知第二批所购件数是第一批所购件数的一半,且每件商品的进价比第一批的进价少10元.(1)、求商场第二批商品A的进价;(2)、商场同时销售另一种热销商品B,已知商品B的进价与第二批商品A的进价相同,且最初销售价为165元,每天能卖出125件,经市场销售发现,若售价每上涨1元,其每天销售量就减少5件,问商场该如何定售价,每天才能获得最大利润?并求出每天的最大利润是多少?25. 在 中, , ,点E是直线 上一动点,点D是直线 上动点,点F是直线 上一动点,且 , .(1)、如图1,当点D,E,F分别在 , , 边上时,请你判断线段 , , 之间有怎样的数量关系?请直接写出你的结论;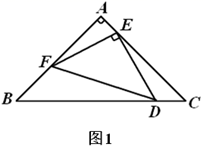 (2)、如图2,当D在 延长线上,E在 延长线上,F在 延长线上时,(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请判断线段 , , 之间有怎样的数量关系?并证明你的结论;
(2)、如图2,当D在 延长线上,E在 延长线上,F在 延长线上时,(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请判断线段 , , 之间有怎样的数量关系?并证明你的结论;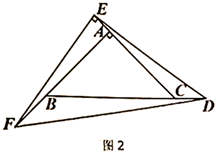 (3)、若 ,当 时,请直接写出 的长.
(3)、若 ,当 时,请直接写出 的长.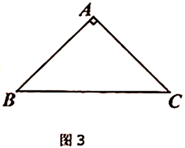 26. 如图,在平面直角坐标系中,抛物线 与x轴交于 和 ,与y轴交于点C.
26. 如图,在平面直角坐标系中,抛物线 与x轴交于 和 ,与y轴交于点C. (1)、求该抛物线的解析式;(2)、绕点A旋转的直线 : 与y轴相交于点D,与抛物线相交于点E,且满足 时,求直线l的解析式;(3)、点P为抛物线上的一点,点Q为抛物线对称轴上的一点,是否存在以点B,C,P,Q为顶点的平行四边形,若存在,请直接写出点P的坐标:若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、绕点A旋转的直线 : 与y轴相交于点D,与抛物线相交于点E,且满足 时,求直线l的解析式;(3)、点P为抛物线上的一点,点Q为抛物线对称轴上的一点,是否存在以点B,C,P,Q为顶点的平行四边形,若存在,请直接写出点P的坐标:若不存在,请说明理由.