辽宁省辽阳市2020年数学中考四模试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
1. 的倒数是( )A、-2 B、2 C、 D、2. 下列图形中既是轴对称图形又是中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是由4个完全相同的小正方体组成的立体图形,它的左视图是( )
A、1个 B、2个 C、3个 D、4个3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是由4个完全相同的小正方体组成的立体图形,它的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 在一个不透明的布袋中装有若干个只有颜色不同的小球,如果袋中有红球5个,黄球4个,其余为白球,从袋子中随机摸出一个球,“摸出黄球”的概率为 ,则袋子中白球的个数为( )A、12 B、5 C、4 D、36. 暑假快到了,为了人同学们过一个有意义的假期,老师推荐给大家一本好书.已知小芳每天比小丽多看5页书,并且小芳看80页书所用的天数与小丽看70页书所用的天数相等,若设小芳每天看书 页,则根据题意课可列出方程为( )A、 B、 C、 D、7. 如图,在 中, ,以顶点A为圆心,适当长为半径画弧,分别交 , 于点M,N,再分别以点M,N为圆心,大于 的长为半径画弧,两弧交于点P,作射线 交边 于点D,若 , ,则 的面积是 ( )
5. 在一个不透明的布袋中装有若干个只有颜色不同的小球,如果袋中有红球5个,黄球4个,其余为白球,从袋子中随机摸出一个球,“摸出黄球”的概率为 ,则袋子中白球的个数为( )A、12 B、5 C、4 D、36. 暑假快到了,为了人同学们过一个有意义的假期,老师推荐给大家一本好书.已知小芳每天比小丽多看5页书,并且小芳看80页书所用的天数与小丽看70页书所用的天数相等,若设小芳每天看书 页,则根据题意课可列出方程为( )A、 B、 C、 D、7. 如图,在 中, ,以顶点A为圆心,适当长为半径画弧,分别交 , 于点M,N,再分别以点M,N为圆心,大于 的长为半径画弧,两弧交于点P,作射线 交边 于点D,若 , ,则 的面积是 ( )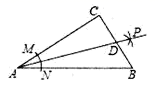 A、15 B、30 C、45 D、608. 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
A、15 B、30 C、45 D、608. 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )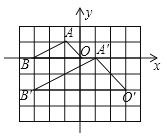 A、(0,0) B、(0,1) C、(﹣3,2) D、(3,﹣2)9. 如图, 与x轴交于点 , ,与 轴的正半轴交于点 .若 ,则点 的纵坐标为( )
A、(0,0) B、(0,1) C、(﹣3,2) D、(3,﹣2)9. 如图, 与x轴交于点 , ,与 轴的正半轴交于点 .若 ,则点 的纵坐标为( )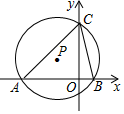 A、 B、 C、 D、10. 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③4a﹣2b+c<0;④8a+c>0.其中正确的有 ( )
A、 B、 C、 D、10. 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b﹣2a=0;②abc<0;③4a﹣2b+c<0;④8a+c>0.其中正确的有 ( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 据统计,2020年中国人口数量约为1424000000人,将1424000000人用科学记数法表示为人.12. 函数y= 的自变量x的取值范围是 .13. 已知数据:﹣1,4,2,﹣2,x的众数是2,那么这组数据的平均数为 .
14. 已知关于x的不等式组 只有两个整数解,则a的取值范围.15. 如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为米. 16. 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= 的图象上.若点B在反比例函数y= 的图象上,则k的值为.
16. 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= 的图象上.若点B在反比例函数y= 的图象上,则k的值为.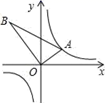 17. 如图,在等边三角形 中, 于点D,点 分别是 上的动点,沿 所在直线折叠 ,使点 落在 上的点 处,当 是直角三角形时, 的值为.
17. 如图,在等边三角形 中, 于点D,点 分别是 上的动点,沿 所在直线折叠 ,使点 落在 上的点 处,当 是直角三角形时, 的值为. 18. 如图,在平面直角坐标系中,直线l1:y=x,直线l2:y=x,在直线l1上取一点B,使OB=1,以点B为对称中心,作点O的对称点B1 , 过点B1作B1A1∥l2 , 交x轴于点A1 , 作B1C1∥x轴,交直线l2于点C1 , 得到四边形OA1B1C1;再以点B1为对称中心,作O点的对称点B2 , 过点B2作B2A2∥l2 , 交x轴于点A2 , 作B2C2∥x轴,交直线l2于点C2 , 得到四边形OA2B2C2;…;按此规律作下去,则四边形OAnBnCn的面积是 .
18. 如图,在平面直角坐标系中,直线l1:y=x,直线l2:y=x,在直线l1上取一点B,使OB=1,以点B为对称中心,作点O的对称点B1 , 过点B1作B1A1∥l2 , 交x轴于点A1 , 作B1C1∥x轴,交直线l2于点C1 , 得到四边形OA1B1C1;再以点B1为对称中心,作O点的对称点B2 , 过点B2作B2A2∥l2 , 交x轴于点A2 , 作B2C2∥x轴,交直线l2于点C2 , 得到四边形OA2B2C2;…;按此规律作下去,则四边形OAnBnCn的面积是 .
三、解答题
-
19. 先化简,再求值: ,其中20. 某中学为做好学生“午餐工程”工作,学校工作人员搭配了A,B,C,D四种不同种类的套餐,学校决定围绕“在A,B,C,D四种套餐中,你最喜欢的套餐种类是什么?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查问适当整理后绘制成如图所示的不完整的条形统计图,其中最喜欢D种套餐的学生占被抽取人数的20%.请你根据以上信息解答下列问题:
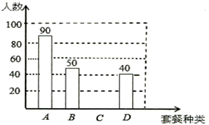
最喜欢的套餐种类的人数发布情况
(1)、在这次调查中,一共抽取了名学生;(2)、通过计算,补全条形统计图;(3)、如果全校有2000名学生,请你估计全校学生中最喜欢 种套餐的学生有多少名?(4)、甲、乙两名同学一起去学校餐厅就餐,他们随机在“A,B,C,D四种套餐”中选择一种,求甲、乙两名同学选择同一种套餐就餐的概率.21. 近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.(1)、求每台A种、B种设备各多少万元?(2)、根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?22. 如图,直线y=x+m与双曲线y= 相交于A(2,1),B两点. (1)、求出一次函数与反比例函数的解析式,并求出B点坐标;(2)、若P为直线x= 上一点,当△APB的面积为6时,请求出点P的坐标.23. (2016·黄冈)东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为:
(1)、求出一次函数与反比例函数的解析式,并求出B点坐标;(2)、若P为直线x= 上一点,当△APB的面积为6时,请求出点P的坐标.23. (2016·黄冈)东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为:,且其日销售量y(kg)与时间t(天)的关系如下表:
时间t(天)
1
3
6
10
20
…
日销售量y(kg)
118
114
108
100
80
…
(1)、已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?(2)、问哪一天的销售利润最大?最大日销售利润为多少?(3)、在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.24. 如图,在 中, , 是 的角平分线, 平分 交 于点E,点O在 边上,以点O为圆心的 经过B、E两点,交 于点F. (1)、求证: 是 的切线;(2)、若 , ,求阴影部分的面积.25. 如图
(1)、求证: 是 的切线;(2)、若 , ,求阴影部分的面积.25. 如图 (1)、问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
(1)、问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.(发现证明)小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
(2)、(类比引申)如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足关系时,仍有EF=BE+FD.(3)、(探究应用)如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40( ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: =1.41, =1.73)26. 如图1,在平面直角坐标系中,抛物线 交x轴于A、B两点,交y轴于点C,且 、 . (1)、求该抛物线的表达式及顶点D的坐标;(2)、若点M是x轴上的一个动点,设 的面积为S,动点M的坐标为 ,令 ,当 时,Q是否有最小值?若有,请求出Q的最小值和此时 的值;若没有,请说明理由;(3)、在抛物线上有一个动点P,y轴上有一个动点N,使得以A、B、P、N为顶点的四边形是平行四边形,请直接写出点P的坐标.
(1)、求该抛物线的表达式及顶点D的坐标;(2)、若点M是x轴上的一个动点,设 的面积为S,动点M的坐标为 ,令 ,当 时,Q是否有最小值?若有,请求出Q的最小值和此时 的值;若没有,请说明理由;(3)、在抛物线上有一个动点P,y轴上有一个动点N,使得以A、B、P、N为顶点的四边形是平行四边形,请直接写出点P的坐标.