辽宁省锦州市黑山县2020年数学中考一模试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
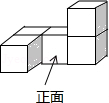
1. 中国人最早使用负数,可追溯到两千多年前的秦汉时期, 的相反数是( )A、2020 B、-2020 C、 D、2. 如图是一个由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、a4+a2=a6 B、a6÷a2=a3 C、a2•a3=a6 D、(﹣2ab2)3=﹣8a3b64. 某班体育委员记录了第一小组七名同学定点投篮(每人投10个)的情况,投进篮框的个数为7,10,5,3,4,9,4,这组数据的众数和平均数分别是( )A、4,6 B、4,5 C、5,4 D、5,65. 如图,数轴上点A,B分别对应实数1,2,过点B作 ,以点B为圆心, 长为半径画弧,交 于点C,以点A为圆心, 长为半径画弧,交数轴于点M,则点M对应的实数的平方是( )
3. 下列运算正确的是( )A、a4+a2=a6 B、a6÷a2=a3 C、a2•a3=a6 D、(﹣2ab2)3=﹣8a3b64. 某班体育委员记录了第一小组七名同学定点投篮(每人投10个)的情况,投进篮框的个数为7,10,5,3,4,9,4,这组数据的众数和平均数分别是( )A、4,6 B、4,5 C、5,4 D、5,65. 如图,数轴上点A,B分别对应实数1,2,过点B作 ,以点B为圆心, 长为半径画弧,交 于点C,以点A为圆心, 长为半径画弧,交数轴于点M,则点M对应的实数的平方是( )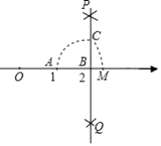 A、2 B、5 C、 D、6. 若关于x的一元二次方程 有两个实数根,则k的取值范围是( )A、 B、 C、 D、7. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中结论正确的有( )
A、2 B、5 C、 D、6. 若关于x的一元二次方程 有两个实数根,则k的取值范围是( )A、 B、 C、 D、7. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中结论正确的有( )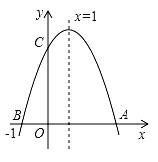 A、①③ B、①④ C、①② D、①③④8. 如图,Rt△ABC中,AB=4,BC=2,正方形ADEF的边长为2,F、A、B在同一直线上,正方形ADEF向右平移到点F与B重合,点F的平移距离为x,平移过程中两图重叠部分的面积为y,则y与x的关系的函数图象表示正确的是( )
A、①③ B、①④ C、①② D、①③④8. 如图,Rt△ABC中,AB=4,BC=2,正方形ADEF的边长为2,F、A、B在同一直线上,正方形ADEF向右平移到点F与B重合,点F的平移距离为x,平移过程中两图重叠部分的面积为y,则y与x的关系的函数图象表示正确的是( )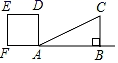 A、
A、 B、
B、 C、
C、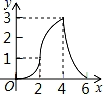 D、
D、
二、填空题
-
9. 分解因式: .10. 从辽宁省工商联获悉,自新型冠状病毒引发的肺炎疫情出现以来,截止2月13日下午6点,全省民营企业、商会及企业家个人累计7412家(人),共向武汉等疫情严重地区及我省定点防治新冠肺炎的医院、政府部门、执勤卡点等捐赠物款约10.1亿元.10.1亿用科学记数法表示应为.11. 如图,直线AB∥CD,直线EF分别交AB、CD于E、F两点,EG平分∠AEF交CD于点G,如果∠2=64°,那么∠1的度数是.
 12. 辽宁省将在2020年底前实现县城以上城区5G全覆盖.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输500兆数据,5G网络比4G网络快45秒,求这两种网络的峰值速率.设5G网络的峰值速率为每秒传输x兆数据,依题意列方程为.13. 如图,在⊙O中,半径OC垂直弦AB于D,点E在⊙O上,∠E=22.5°,AB=2,则半径OB等于.
12. 辽宁省将在2020年底前实现县城以上城区5G全覆盖.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输500兆数据,5G网络比4G网络快45秒,求这两种网络的峰值速率.设5G网络的峰值速率为每秒传输x兆数据,依题意列方程为.13. 如图,在⊙O中,半径OC垂直弦AB于D,点E在⊙O上,∠E=22.5°,AB=2,则半径OB等于. 14. 如图,在平面直角坐标系xOy中,一次函数y=﹣x+4的图象与反比例函数y= (k>0)的图象相交于A,B两点,与x轴相交于点C,连接OB,且 BOC的面积为2.则k=.
14. 如图,在平面直角坐标系xOy中,一次函数y=﹣x+4的图象与反比例函数y= (k>0)的图象相交于A,B两点,与x轴相交于点C,连接OB,且 BOC的面积为2.则k=. 15. 如图,在矩形纸片ABCD中,AB=4,BC=4 ,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是.
15. 如图,在矩形纸片ABCD中,AB=4,BC=4 ,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是.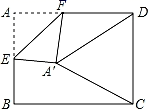 16. 已知:如图,在平面直角坐标系中,点B的坐标为(1,0),以OB为边,在第一象限内作等边三角形OAB,过点A作AB的垂线,交x轴于点 ,过点 作 的垂线,交y轴于点 ,过点 作 的垂线,交x轴于点 ,过点 作 的垂线,交y轴于点 ,…,这样一直作下去,则点 的坐标为.
16. 已知:如图,在平面直角坐标系中,点B的坐标为(1,0),以OB为边,在第一象限内作等边三角形OAB,过点A作AB的垂线,交x轴于点 ,过点 作 的垂线,交y轴于点 ,过点 作 的垂线,交x轴于点 ,过点 作 的垂线,交y轴于点 ,…,这样一直作下去,则点 的坐标为.
三、解答题
-
17. 先化简代数式( )× ,请你选取一个使原分式有意义的x值,代入求值.18. 某校为了了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱的乐器),现将收集到的数据绘制成如下两幅不完整的统计图.
 (1)、这次共抽取学生调查,扇形统计图中的x=;(2)、请补全统计图;(3)、在扇形统计图中“扬琴”所对扇形的圆心角是多少度;(4)、若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有多少名.19. 七巧板是我国流传已久的一种智力玩具.小鹏在玩七巧板时用它画成了3幅图案并将它贴在3张完全相同的不透明卡片上,如图.小鹏将这3张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,放回后洗匀,再随机抽取一张卡片.请你用列表法或画树状图(树形图)法,帮助小鹏求出两张卡片上的图案都是小动物的概率(卡片名称可用字母表示).
(1)、这次共抽取学生调查,扇形统计图中的x=;(2)、请补全统计图;(3)、在扇形统计图中“扬琴”所对扇形的圆心角是多少度;(4)、若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有多少名.19. 七巧板是我国流传已久的一种智力玩具.小鹏在玩七巧板时用它画成了3幅图案并将它贴在3张完全相同的不透明卡片上,如图.小鹏将这3张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,放回后洗匀,再随机抽取一张卡片.请你用列表法或画树状图(树形图)法,帮助小鹏求出两张卡片上的图案都是小动物的概率(卡片名称可用字母表示). 20. 某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万kg与3.6万kg,现假定该养殖场蛋鸡产蛋量的月增长率相同.(1)、求该养殖场蛋鸡产蛋量的月平均增长率;(2)、假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万kg.如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?21. 如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了5.2米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1:2.4,求建筑物AB的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
20. 某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万kg与3.6万kg,现假定该养殖场蛋鸡产蛋量的月增长率相同.(1)、求该养殖场蛋鸡产蛋量的月平均增长率;(2)、假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万kg.如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?21. 如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了5.2米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1:2.4,求建筑物AB的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51) 22. 如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP,AE.
22. 如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP,AE. (1)、判断直线PQ与⊙O的关系;(2)、若直径AB的长为4.当四边形AEOP为菱形时,求PE的长.23. 某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如图.
(1)、判断直线PQ与⊙O的关系;(2)、若直径AB的长为4.当四边形AEOP为菱形时,求PE的长.23. 某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如图. (1)、求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;(2)、当每件产品的销售价定为多少元时,此时每日的销售利润最多,最多是多少元.24. 如图,将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)、求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;(2)、当每件产品的销售价定为多少元时,此时每日的销售利润最多,最多是多少元.24. 如图,将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F. (1)、求证:AF+EF=DE.(2)、若将图①中的△DBE绕点B按顺时针方向旋转α,且0°<α<60°,其他条件不变,请在图②中画出旋转后的图形,并直接写出(1)中的结论是否仍然成立.(3)、若将图①中的△DBE绕点B按顺时针方向旋转β,且60°<β<180°,其他条件不变,如图③.你认为(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请写出AF,EF与DE之间的关系,并说明理由.25. 如图,抛物线y=- x2+bx+c与x轴交于A、B两点,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(1)、求证:AF+EF=DE.(2)、若将图①中的△DBE绕点B按顺时针方向旋转α,且0°<α<60°,其他条件不变,请在图②中画出旋转后的图形,并直接写出(1)中的结论是否仍然成立.(3)、若将图①中的△DBE绕点B按顺时针方向旋转β,且60°<β<180°,其他条件不变,如图③.你认为(1)中的结论还成立吗?若成立,请写出证明过程;若不成立,请写出AF,EF与DE之间的关系,并说明理由.25. 如图,抛物线y=- x2+bx+c与x轴交于A、B两点,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD. (1)、求抛物线的表达式及对称轴;(2)、点F是抛物线上的动点,当∠FBA=2∠BDE时,求点F的坐标;(3)、若点P是x轴上方抛物线上的动点,以PB为边作正方形PBGH,随着点P的运动,正方形的大小、位置也随着改变,当顶点G或H恰好落在y轴上时,请直接写出点P的横坐标.
(1)、求抛物线的表达式及对称轴;(2)、点F是抛物线上的动点,当∠FBA=2∠BDE时,求点F的坐标;(3)、若点P是x轴上方抛物线上的动点,以PB为边作正方形PBGH,随着点P的运动,正方形的大小、位置也随着改变,当顶点G或H恰好落在y轴上时,请直接写出点P的横坐标.