辽宁省大连市中山区2020年数学中考二模试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
1. 下列几何体中,其俯视图与主视图完全相同的是( )A、
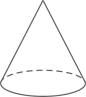 B、
B、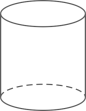 C、
C、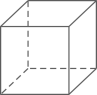 D、
D、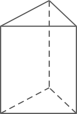 2. 一5的绝对值是( )A、5 B、 C、 D、-53. 在平面直角坐标系中,将点 向右平移 个单位长度后得到的点的坐标为( )A、 B、 C、 D、4. 不等式3x+2≥5的解集是( )A、x≥1 B、x≥ C、x≤1 D、x≤﹣15. 下列各式运算正确的是( )A、 B、 C、 D、6. 现有四个外观完全一样的粽子,其中有且只有一个有蛋黄.若从中一次随机取出两个,则这两个粽子都没有蛋黄的概率是( )A、 B、 C、 D、7. 如图,把一块等腰直角三角板的直角顶点放在直尺的一边上,如果∠1=40°,那么∠2=( )
2. 一5的绝对值是( )A、5 B、 C、 D、-53. 在平面直角坐标系中,将点 向右平移 个单位长度后得到的点的坐标为( )A、 B、 C、 D、4. 不等式3x+2≥5的解集是( )A、x≥1 B、x≥ C、x≤1 D、x≤﹣15. 下列各式运算正确的是( )A、 B、 C、 D、6. 现有四个外观完全一样的粽子,其中有且只有一个有蛋黄.若从中一次随机取出两个,则这两个粽子都没有蛋黄的概率是( )A、 B、 C、 D、7. 如图,把一块等腰直角三角板的直角顶点放在直尺的一边上,如果∠1=40°,那么∠2=( )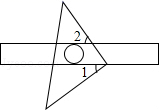 A、40° B、45° C、50° D、60°8. 用一条长40cm的绳子围成一个面积为64cm2的长方形.设长方形的长为xcm,则可列方程为( )A、x(20+x)=64 B、x(20﹣x)=64 C、x(40+x)=64 D、x(40﹣x)=649. 如图,在平行四边形 中, , , ,则 的长是( )
A、40° B、45° C、50° D、60°8. 用一条长40cm的绳子围成一个面积为64cm2的长方形.设长方形的长为xcm,则可列方程为( )A、x(20+x)=64 B、x(20﹣x)=64 C、x(40+x)=64 D、x(40﹣x)=649. 如图,在平行四边形 中, , , ,则 的长是( )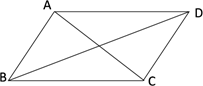 A、 B、 C、3 D、510. 已知 ,二次函数 的图象为下列之一,则a的值为( )
A、 B、 C、3 D、510. 已知 ,二次函数 的图象为下列之一,则a的值为( )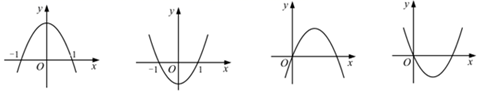 A、1 B、-1 C、 D、
A、1 B、-1 C、 D、二、填空题
-
11. 数据2,7,5,7,9的众数是 。12. 如图,小亮为了测量校园里教学楼 的高度,将测角仪 竖直放置在与教学楼水平距离为 的地面上,若测角仪的高度为 ,测得教学楼的顶部A处的仰角为 ,则教学楼的高度是 .
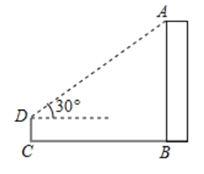 13. 中国的《九章算术》是世界现代数学的两大源泉之一,其中有一问题:“今有牛五,羊二,值金十两.牛二,羊五,值金八两.问牛羊各值金几何?”译文:今有牛5头,羊2头,共值金10两,牛2头,羊5头,共值金8两.问牛、羊每头各值金多少?设牛、羊每头各值金 两、 两,依题意,可列出方程为 .14. 如图,点A、B、C在 上, , ,则 的半径为.
13. 中国的《九章算术》是世界现代数学的两大源泉之一,其中有一问题:“今有牛五,羊二,值金十两.牛二,羊五,值金八两.问牛羊各值金几何?”译文:今有牛5头,羊2头,共值金10两,牛2头,羊5头,共值金8两.问牛、羊每头各值金多少?设牛、羊每头各值金 两、 两,依题意,可列出方程为 .14. 如图,点A、B、C在 上, , ,则 的半径为. 15. 如图,点A在反比例函数 图象上,点B、C在反比例函数 图象上,且 轴, 轴,若点C的纵坐标为2,则 的长度为.
15. 如图,点A在反比例函数 图象上,点B、C在反比例函数 图象上,且 轴, 轴,若点C的纵坐标为2,则 的长度为.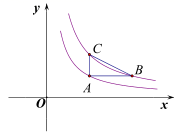 16. 在 中, , ,D为 中点,E为 上一点(不与点A、C重合),连接 、 交于点F, .设 , .则y关于x的函数解析式为.
16. 在 中, , ,D为 中点,E为 上一点(不与点A、C重合),连接 、 交于点F, .设 , .则y关于x的函数解析式为.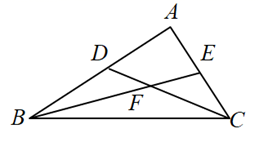
三、解答题
-
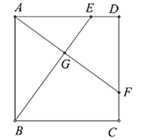
17. 计算: .18. 化简: .19. 如图,正方形 ,点 分别在 , 上,且 , 与 相交于点G.求证: .
 20. 为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了部分学生,调查了他们平均每天的睡眠时间(单位:h).以下是根据调查结果绘制的统计图表的一部分.
20. 为了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了部分学生,调查了他们平均每天的睡眠时间(单位:h).以下是根据调查结果绘制的统计图表的一部分.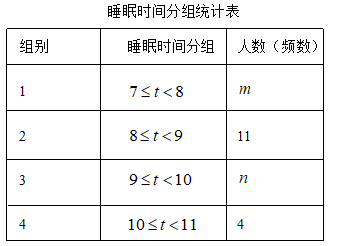
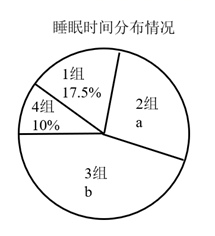
请根据以上信息,解答下列问题:
(1)、共随机抽取名学生;(2)、 , , , ;(3)、抽取的这40名学生平均每天睡眠时间的中位数落在组(填组别);(4)、如果按照学校要求,学生平均每天的睡眠时间应不少于 ,请估计该校学生中睡眠时间符合要求的人数.21. 端午节前后,张阿姨两次到超市购买同一种粽子.节前,按标价购买,用了96元;节后,按标价的6折购买,用了72元,两次一共购买了27个.这种粽子的标价是多少?22. 已知: 为 的直径,C为圆弧上一点, 垂直于过C点的切线,垂足为D, 的延长线交直线 于点E. ,垂足为点F.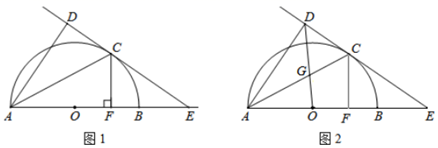 (1)、如图1,求证: ;(2)、如图2,若 ,连接 交 于点G,且 时,求 的长度.23. 为缓解油价上涨给出租车行业带来的成本压力,某市调整出租车运价,调整方案见下列表格及图象(其中a、b、c为常数):
(1)、如图1,求证: ;(2)、如图2,若 ,连接 交 于点G,且 时,求 的长度.23. 为缓解油价上涨给出租车行业带来的成本压力,某市调整出租车运价,调整方案见下列表格及图象(其中a、b、c为常数):行驶路程
收费标准
调价前
调价后
不超出 的部分
起步价9元
起步价a元
超出 不超出 的部分
每公里2元
每公里b元
超出 的部分
每公里c元

设行驶路程为 时,调价前的运价为 (元),调价后的运价为 (元).如图,折线 表示 与x之间的函数关系;线段 表示 时, 与x之间的函数关系.根据图表信息,完成下列各题:
(1)、填空: , , ;(2)、写出当 时, 与x之间的函数关系式,并在上图中画出该函数图象;(3)、当行驶路程为 时,讨论调价前后运价的高低.24. 在平面直角坐标系中,直线 与x轴、y轴分别交于点B、A,动点C以每秒2个单位长度的速度从点B向终点O运动,过点 作 ,交直线 于点D.设 ,将 绕点 顺时针旋转 得到线段 ,连接 .设四边形 与 的重叠部分面积为 (平方单位), ,点C的运动时间为t秒.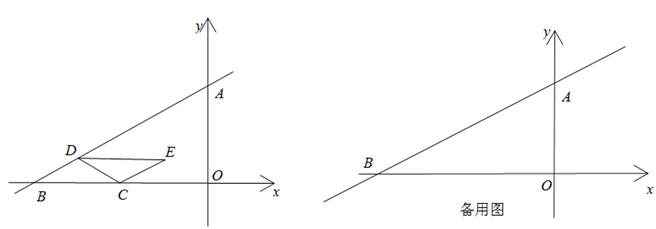 (1)、求 的长;(2)、求证:四边形 是平行四边形;(3)、求S与t的函数关系式,并直接写出自变量取值范围.25. 如图,在 中, 为边 上的中线,点D为 延长线上一点,连接 交 于点E, , .
(1)、求 的长;(2)、求证:四边形 是平行四边形;(3)、求S与t的函数关系式,并直接写出自变量取值范围.25. 如图,在 中, 为边 上的中线,点D为 延长线上一点,连接 交 于点E, , .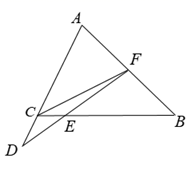 (1)、求证: ;(2)、在图中找出与 相等的线段,并证明;(3)、若 ,求 的值(用含k的代数式表示).26. 定义:函数 与 的图象关于 轴对称,点 是x轴上一点,将函数 的图象位于直线 左侧的部分,以x轴为对称轴翻折,得到新的函数w的图象,我们称函数w是函数l的对称折函数,函数w的图象记作 ,函数l的图象位于直线 上以及右侧的部分记作 ,图象 和 合起来记作图象F.
(1)、求证: ;(2)、在图中找出与 相等的线段,并证明;(3)、若 ,求 的值(用含k的代数式表示).26. 定义:函数 与 的图象关于 轴对称,点 是x轴上一点,将函数 的图象位于直线 左侧的部分,以x轴为对称轴翻折,得到新的函数w的图象,我们称函数w是函数l的对称折函数,函数w的图象记作 ,函数l的图象位于直线 上以及右侧的部分记作 ,图象 和 合起来记作图象F.例如:如图,函数l的解析式为 ,当 时,它的对称折函数w的解析式为 .
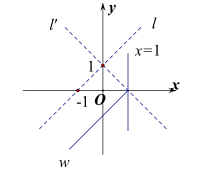 (1)、函数l的解析式为 ,当 时,它的对称折函数w的解析式为;(2)、函数l的解析式为 ,当 且 时,求图象F上点的纵坐标的最大值和最小值;(3)、函数 的解析式为 .若 ,直线 与图象F有两个公共点,求t的取值范围.
(1)、函数l的解析式为 ,当 时,它的对称折函数w的解析式为;(2)、函数l的解析式为 ,当 且 时,求图象F上点的纵坐标的最大值和最小值;(3)、函数 的解析式为 .若 ,直线 与图象F有两个公共点,求t的取值范围.