湖北省襄阳市保康县2020年数学中考适应性试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
1. -3的倒数是( )A、3 B、-3 C、 D、2. 2019年,保康县全年投入资金3593万元,实施学校建设项目16个,新建、改扩建校舍20398平方米.其中20398m2用科学记数法可表示为( )A、 20.4×103m2 B、2.03×104m2 C、2.04×104m2 D、3.60×103万元3. 如图,直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α的余角等于( )
 A、19° B、38° C、42° D、52°4. 下列计算正确的是( )A、3x2y+5xy=8x3y2 B、(x+y)2=x+y C、(-2x)2÷x=4x D、a6÷a3=a25. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A、19° B、38° C、42° D、52°4. 下列计算正确的是( )A、3x2y+5xy=8x3y2 B、(x+y)2=x+y C、(-2x)2÷x=4x D、a6÷a3=a25. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )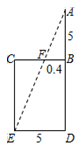 A、1.25尺 B、56.5尺 C、6.25尺 D、57.5尺6. 如图,在Rt△ABC中,AC=5cm,BC=12cm,∠ACB=90°,把Rt△ABC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为( )
A、1.25尺 B、56.5尺 C、6.25尺 D、57.5尺6. 如图,在Rt△ABC中,AC=5cm,BC=12cm,∠ACB=90°,把Rt△ABC所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为( )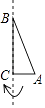 A、60πcm2 B、65πcm2 C、120πcm2 D、130πcm27. 某中学对该校九年级45名女学生进行了一次立定跳远测试,成绩如表:
A、60πcm2 B、65πcm2 C、120πcm2 D、130πcm27. 某中学对该校九年级45名女学生进行了一次立定跳远测试,成绩如表:跳远成绩
160
170
180
190
200
210
人数
3
9
6
9
15
3
这些立定跳远成绩的中位数和众数分别是( )
A、9,9 B、15,9 C、190,200 D、185,2008. 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )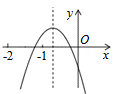 A、a<0 B、b<0 C、c<0 D、a<b9. 如图,EF过▱ABCD对角线的交点O,交AD于E,交BC于F,若▱ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )
A、a<0 B、b<0 C、c<0 D、a<b9. 如图,EF过▱ABCD对角线的交点O,交AD于E,交BC于F,若▱ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( ) A、14 B、13 C、12 D、1010. 如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3 ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
A、14 B、13 C、12 D、1010. 如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3 ),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )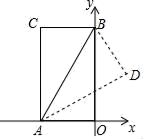 A、( , ) B、(2, ) C、( , ) D、( ,3﹣ )
A、( , ) B、(2, ) C、( , ) D、( ,3﹣ )二、填空题
-
11. 分解因式: =.12. 已知一元二次方程x2-3x-2=0的两个实数根为x1 , x2 , 则(x1-1)(x2-1)的值是.13. 经过某十字路口的汽车,可直行,也可向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过该十字路口时都直行的概率是 .14. 如图,在 中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与 相交于点F.若 的长为 ,则图中阴影部分的面积为.
 15. 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cos∠α= ,下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或 ;④0<CE≤6.4.其中正确的结论是.(把你认为正确结论的序号都填上)
15. 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cos∠α= ,下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或 ;④0<CE≤6.4.其中正确的结论是.(把你认为正确结论的序号都填上)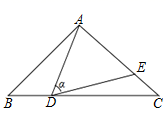 16. 如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是.
16. 如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是.
三、解答题
-
17. 化简:( )÷ .18. 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别
A
B
C
D
E
类型
新闻
体育
动画
娱乐
戏曲
人数
11
20
40
m
4
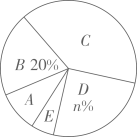
请你根据以上信息,回答下列问题:
(1)、统计表中m的值为 , 统计图中n的值为 , A类对应扇形的圆心角为度;(2)、该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;(3)、样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.19. 为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度 ,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部 的仰角为 ,同时测得教学楼窗户D处的仰角为 (A、B、D、E在同一直线上).然后,小明沿坡度 的斜坡从C走到F处,此时 正好与地面 平行. (1)、求点F到直线 的距离(结果保留根号);(2)、若小明在F处又测得宣传牌顶部A的仰角为 ,求宣传牌的高度 (结果精确到0.1米, , ).20. 如图,一次函数y=kx+b与反比例函数y= 的图象相交于A(2,4)、B(-4,n)两点.
(1)、求点F到直线 的距离(结果保留根号);(2)、若小明在F处又测得宣传牌顶部A的仰角为 ,求宣传牌的高度 (结果精确到0.1米, , ).20. 如图,一次函数y=kx+b与反比例函数y= 的图象相交于A(2,4)、B(-4,n)两点. (1)、分别求出一次函数与反比例函数的表达式;(2)、根据所给条件,请直接写出不等式kx+b> 的解集;(3)、过点B作BC⊥x轴,垂足为点C,连接AC,求S△ABC.21. 春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
(1)、分别求出一次函数与反比例函数的表达式;(2)、根据所给条件,请直接写出不等式kx+b> 的解集;(3)、过点B作BC⊥x轴,垂足为点C,连接AC,求S△ABC.21. 春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
22. 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F. (1)、求证:DF是⊙O的切线;(2)、若AE=4,cosA= ,求DF的长.23. 某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象(如图),图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)、求证:DF是⊙O的切线;(2)、若AE=4,cosA= ,求DF的长.23. 某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象(如图),图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件. (1)、第24天的日销售量是件,日销售利润是元;(2)、求y与x之间的函数关系式,并写出x的取值范围;(3)、日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元?24. 如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.
(1)、第24天的日销售量是件,日销售利润是元;(2)、求y与x之间的函数关系式,并写出x的取值范围;(3)、日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元?24. 如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N. (1)、(问题引入)若点O是AC的中点, ,求 的值;温馨提示:过点A作MN的平行线交BN的延长线于点G.(2)、(探索研究)若点O是AC上任意一点(不与A,C重合),求证: ;(3)、(拓展应用)如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若 , ,求 的值.25. 如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)、(问题引入)若点O是AC的中点, ,求 的值;温馨提示:过点A作MN的平行线交BN的延长线于点G.(2)、(探索研究)若点O是AC上任意一点(不与A,C重合),求证: ;(3)、(拓展应用)如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若 , ,求 的值.25. 如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C. (1)、求抛物线的函数表达式;(2)、如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;(3)、若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
(1)、求抛物线的函数表达式;(2)、如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;(3)、若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.