广东省汕头市龙湖区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-08-10 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分
-
1. 计算
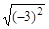 =( ) A、 9 B、 3 C、-3 D、±32. 下列选项中,是直角三角形的三边长的是( )A、 1,2,3 B、 2,3,4 C、 3,4,5 D、 4,5,63. 下列哪个点在正比例函数
=( ) A、 9 B、 3 C、-3 D、±32. 下列选项中,是直角三角形的三边长的是( )A、 1,2,3 B、 2,3,4 C、 3,4,5 D、 4,5,63. 下列哪个点在正比例函数 的图像上( ) A、(2,0) B、(-2,0) C、(2,1) D、(-1,-2)4. 在参加今年体育中考前,甲、乙两名同学各作了5次立定跳远测试,两人的平均成绩相同,所测得成绩的方差分别是 =2.4, =5.2,那么( )A、甲的成绩更稳定 B、乙的成绩更稳定 C、甲、乙的成绩一样稳定 D、不能确定谁的成绩更稳定5. 下列二次根式是最简二次根式的是( ).A、 B、 C、 D、6. 如图,已知正方形B的面积为144,正方形C的面积为169,那么正方形A的面积为( )
的图像上( ) A、(2,0) B、(-2,0) C、(2,1) D、(-1,-2)4. 在参加今年体育中考前,甲、乙两名同学各作了5次立定跳远测试,两人的平均成绩相同,所测得成绩的方差分别是 =2.4, =5.2,那么( )A、甲的成绩更稳定 B、乙的成绩更稳定 C、甲、乙的成绩一样稳定 D、不能确定谁的成绩更稳定5. 下列二次根式是最简二次根式的是( ).A、 B、 C、 D、6. 如图,已知正方形B的面积为144,正方形C的面积为169,那么正方形A的面积为( )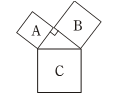 A、313 B、144 C、169 D、257. 如图,□ ABCD中,CE⊥AB,垂足为E,如果∠A=125°,则∠BCE等于( )
A、313 B、144 C、169 D、257. 如图,□ ABCD中,CE⊥AB,垂足为E,如果∠A=125°,则∠BCE等于( )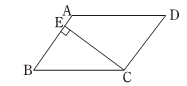 A、55° B、35° C、25° D、30°8. 一次函数 的图象经过的象限是( )A、 一、二、三 B、 二、三、四 C、一、二、四 D、一、三、四9. 如图,在矩形ABCD中,对角线 BD=8cm , ∠AOD=120°,则AB的长为( )
A、55° B、35° C、25° D、30°8. 一次函数 的图象经过的象限是( )A、 一、二、三 B、 二、三、四 C、一、二、四 D、一、三、四9. 如图,在矩形ABCD中,对角线 BD=8cm , ∠AOD=120°,则AB的长为( )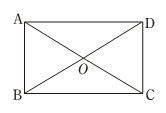 A、
A、 cm
B、2cm
C、2
cm
B、2cm
C、2  cm
D、4 cm
10. 点P(x, y )在第一象限内,且 x+y =6,点 A (4,0).设 的面积为 S ,则下列图像中,能正确反映 S 与之间的函数关系式的图像是( )A、
cm
D、4 cm
10. 点P(x, y )在第一象限内,且 x+y =6,点 A (4,0).设 的面积为 S ,则下列图像中,能正确反映 S 与之间的函数关系式的图像是( )A、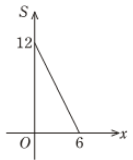 B、
B、 C、
C、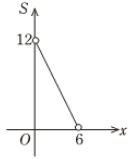 D、
D、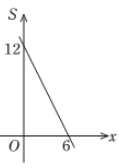
二、填空题(本大题共7小题,每小题4分,共28分
-
11. 在式子
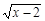 中,的取值范围是 .
12. 已知一次函数 , 随的增大而增大,则 0.(填“>”,“<”或“=”)13. 小明某学期数学平时成绩70分,期中考成绩80分,期末考成绩90分,计算学期总评成绩方法如下:平时成绩占30%,期中成绩占30%,期末成绩占40%,那么小明这学期的数学总评成绩是分.14. 如图,在 中, , , ,则斜边 的长是 .
中,的取值范围是 .
12. 已知一次函数 , 随的增大而增大,则 0.(填“>”,“<”或“=”)13. 小明某学期数学平时成绩70分,期中考成绩80分,期末考成绩90分,计算学期总评成绩方法如下:平时成绩占30%,期中成绩占30%,期末成绩占40%,那么小明这学期的数学总评成绩是分.14. 如图,在 中, , , ,则斜边 的长是 .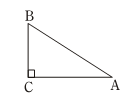 15. 已知 的三边分别为a, b ,c,且a, b 满足 ,c=13,则 = .16. 如图,正方形ABCD的面积为1,则以相邻两边中点连接 EF为边的正方形EFGH的周长为 .
15. 已知 的三边分别为a, b ,c,且a, b 满足 ,c=13,则 = .16. 如图,正方形ABCD的面积为1,则以相邻两边中点连接 EF为边的正方形EFGH的周长为 .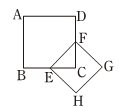 17. 如图,矩形纸片ABCD中,已知 AD=8,折叠纸片使 AB 边与对角线 AC 重合,点 B 落在点 F 处,折痕为 AE , 且 EF=3,则 AB 的长为 .
17. 如图,矩形纸片ABCD中,已知 AD=8,折叠纸片使 AB 边与对角线 AC 重合,点 B 落在点 F 处,折痕为 AE , 且 EF=3,则 AB 的长为 .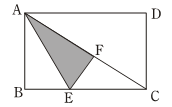
三、解答题(一
-
18. 计算:19. 下表是一次函数 , 、 为常数)的自变量与函数 的对应值:
x -2
0
1
3
0
(1)、根据表格,求一次函数的解析式.(2)、请直接写出 =.20. 在矩形ABCD中,BF=CE,求证:AE=DF.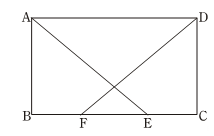
四、解答题(二
-
21. 如图,直线 与直线 交于点M(﹣1,2),与轴分别交于点A,B,与 轴分别交于C,D.
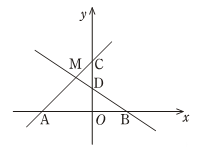 (1)、根据图像写出方程组 的解是.(2)、根据函数图象写出不等式 的解集.(3)、求直线AC,直线BD与轴围成的△ABM的面积.22. 某校在“爱护地球、绿化祖国”的创建活动中,组织学生开展了植树造林活动,为了解全校学生植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
(1)、根据图像写出方程组 的解是.(2)、根据函数图象写出不等式 的解集.(3)、求直线AC,直线BD与轴围成的△ABM的面积.22. 某校在“爱护地球、绿化祖国”的创建活动中,组织学生开展了植树造林活动,为了解全校学生植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:植树数量(棵)
5
6
7
8
10
人数
28
25
10
15
22
(1)、上述数据中,中位数是棵,众数是棵.(2)、若该校有1800名学生,请根据以上调查结果估计该校学生植树总数.23. 如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.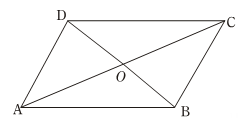 (1)、求证:四边形ABCD是平行四边形;(2)、若AC⊥BD,AC=8,BD=6,
(1)、求证:四边形ABCD是平行四边形;(2)、若AC⊥BD,AC=8,BD=6,求平行四边形ABCD的面积.
五、解答题(三)(本大题共2小题,每小题10分,共20分
-
24. A城有肥料200t,B城有肥料300t,现要把这些肥料全部运往C、D两乡.从A城运往C,D两乡肥料费分别为20元/t和25元/t;从B城往C,D两乡运肥料的费用分别为15元/t和24元/t.现C乡需要肥料240t,D乡需要肥料260t.
设A城运往C乡x,请解答下列问题:
(1)、根据题意,填写下列表格:城、乡/吨数
A
B
C
D
(2)、设总运费为W(元),求出W(元)与(吨)的函数关系式,并写出自变量的取值范围.(3)、求怎么调运可使总运费最少?最少为多少元?25. 如图,在平面直角坐标系中,直线 ∶ 分别与 轴、 轴交于点B、C,且与直线 ∶ 交于点A.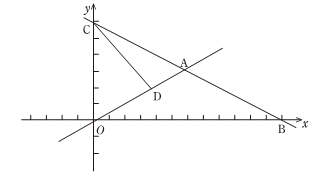 (1)、请写出A( , ),B( , ),C ( , ).(2)、若D是线段OA上的一点,且△COD的面积为12,求直线CD的函数表达式.(3)、在(2)的条件下,设P是射线CD上的点,在平面内存在点Q,使以O、C、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.
(1)、请写出A( , ),B( , ),C ( , ).(2)、若D是线段OA上的一点,且△COD的面积为12,求直线CD的函数表达式.(3)、在(2)的条件下,设P是射线CD上的点,在平面内存在点Q,使以O、C、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.