湖北省武汉市硚口区2020年数学中考二模试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 式子 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、3. 事件A:随意翻看一本书的某页,这页的页码是奇数.事件B:任意画一个三角形,内角和是 .则( )A、事件A和事件B都是必然事件 B、事件A是随机事件,事件B是不可能事件 C、事件A是必然事件,事件 是不可能事件 D、事件A和事件B都是随机事件4. 下列图形中,既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 下图是由八个相同的小正方体组合而成的几何体,其俯视图是( )
5. 下图是由八个相同的小正方体组合而成的几何体,其俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 关于反比例函数 的下列说法:①若其图象在第三、一象限,则 ;②若其图象上两点 、 ,当 时, ,则 ;③其图象与坐标轴没有公共点.其中正确的说法是( )A、① B、①② C、①②③ D、②③7. 疫情防控,我们一直在坚守.某居委会组织两个检查组,分别对“居民体温”和“居民安全出行”的情况进行抽查.若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查,则他们恰好抽到同一个小区的概率是( )A、 B、 C、 D、8. 某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )
6. 关于反比例函数 的下列说法:①若其图象在第三、一象限,则 ;②若其图象上两点 、 ,当 时, ,则 ;③其图象与坐标轴没有公共点.其中正确的说法是( )A、① B、①② C、①②③ D、②③7. 疫情防控,我们一直在坚守.某居委会组织两个检查组,分别对“居民体温”和“居民安全出行”的情况进行抽查.若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查,则他们恰好抽到同一个小区的概率是( )A、 B、 C、 D、8. 某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )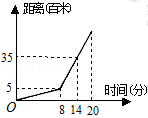 A、仍会迟到2分钟到校 B、刚好按时到校 C、可以提前2分钟到校 D、可以提前5分钟到校9. 如图,点A、B、C、D都在 上, , 为 上的一点, , 的延长线交 于 ,若 ,则 的值为( )
A、仍会迟到2分钟到校 B、刚好按时到校 C、可以提前2分钟到校 D、可以提前5分钟到校9. 如图,点A、B、C、D都在 上, , 为 上的一点, , 的延长线交 于 ,若 ,则 的值为( )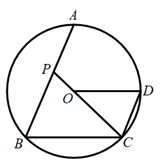 A、2 B、 C、 D、410. 观察下列算式: , , ,…,它有一定的规律性,把第 个算式的结果记为 ,则 的值是( )A、 B、 C、 D、
A、2 B、 C、 D、410. 观察下列算式: , , ,…,它有一定的规律性,把第 个算式的结果记为 ,则 的值是( )A、 B、 C、 D、二、填空题
-
11. 计算 的结果是.12. 某班同学进行数学测试,将所得成绩(整数)进行整理后分成五组,并绘制成如图的频数分布直方图,则这次成绩的中位数落在这一分数段内(填具体分数).
 13. 计算 的结果是.14. 已知一张三角形纸片 如图甲 ,其中 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为 如图乙 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为 如图丙 原三角形纸片ABC中, 的大小为
13. 计算 的结果是.14. 已知一张三角形纸片 如图甲 ,其中 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为 如图乙 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为 如图丙 原三角形纸片ABC中, 的大小为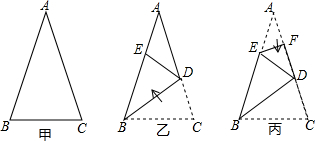 15. 如图,二次函数 的图象与 轴交于 ,对称轴为直线 ,与 轴的交点 在 和 之间(不包括这两个点),下列结论:①当 时, ;② ;③当 时, ;④ .其中正确的结论的序号是.
15. 如图,二次函数 的图象与 轴交于 ,对称轴为直线 ,与 轴的交点 在 和 之间(不包括这两个点),下列结论:①当 时, ;② ;③当 时, ;④ .其中正确的结论的序号是. 16. 如图,在四边形 中, , , , ,则 的长为.
16. 如图,在四边形 中, , , , ,则 的长为.
三、解答题
-
17. 计算:8a6÷2a2+4a3•2a﹣(3a2)218. 如图, ,点C在 上, 交 于点 , , ,求证: .
 19. 为了加强学生课外阅读,开阔视野,某校开展了“书香校园,诵读经典”活动,学校随机抽查了部分学生,对他们每天的课外阅读时间进行调查,并将调查统计的结果分为四类:每天诵读时间 分钟的学生记为A类,20分钟 分钟记为B类,40分钟 分钟记为C类, 分钟记为D类,收集的数据绘制如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
19. 为了加强学生课外阅读,开阔视野,某校开展了“书香校园,诵读经典”活动,学校随机抽查了部分学生,对他们每天的课外阅读时间进行调查,并将调查统计的结果分为四类:每天诵读时间 分钟的学生记为A类,20分钟 分钟记为B类,40分钟 分钟记为C类, 分钟记为D类,收集的数据绘制如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题: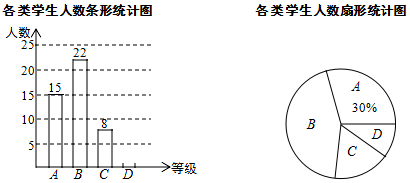 (1)、这次共抽取了名学生进行调查统计,扇形统计图中 类所对应的扇形圆心角大小为;(2)、将条形统计图补充完整;(3)、如果该校共有2000名学生,请你估计该校 类学生约有多少人?20. 如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.点A、B、C、F都是格点.用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示.
(1)、这次共抽取了名学生进行调查统计,扇形统计图中 类所对应的扇形圆心角大小为;(2)、将条形统计图补充完整;(3)、如果该校共有2000名学生,请你估计该校 类学生约有多少人?20. 如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.点A、B、C、F都是格点.用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示. (1)、在图1中,
(1)、在图1中,①画线段 ,使AD∥BC,且 ;
②画 ;
③在线段 上画点 ,使 .
(2)、在图2中,画点M,使点M与点F关于 对称.21. 如图,在 中, ,以 上的一点O为圆心, 为半径作 ,与 切于点D,交 于点E,交 于点F.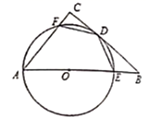 (1)、求证: ;(2)、若 ,求 的值.22. 某公司有A型产品40件, 型产品60件,分配给甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.甲、乙两商店销售A、B型产品每件的利润如下表:
(1)、求证: ;(2)、若 ,求 的值.22. 某公司有A型产品40件, 型产品60件,分配给甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.甲、乙两商店销售A、B型产品每件的利润如下表:A型产品利润(元/件)
B型产品利润(元/件)
甲店
200
170
乙店
160
150
设分配给甲店A型产品x件,公司卖出这100件产品的总利润为w元.
(1)、求w与x的函数关系式;(2)、求总利润w的取值范围;(3)、为了促销,公司决定对甲店销售A型产品让利a元/件,且让利后仍高于甲店销售 型产品的每件利润,请问x为何值时,总利润最大?23. 在正方形 中,点E是 边上的动点,连接 . (1)、如图1,点F在 的延长线上,且 .
(1)、如图1,点F在 的延长线上,且 .①求证: ;
②如图2,将 绕点 逆时针旋转 得到对应 ,射线 交 于N,交 于M,连接 ,试探究 与 之间的数量关系.
(2)、如图3,若 ,点 是 边上的动点,且 ,连接 ,直接写出 的最小值.24. 直线 与 轴、 轴分别交于点B、E,抛物线 经过点 、点B,与y轴交于点C.
 (1)、求抛物线L的解析式;(2)、如图1,点P在y轴上,连接 ,若 ,求点P的坐标;(3)、如图2,将抛物线L平移,使其顶点是坐标原点O,得到抛物线 ,平移直线 经过原点O,交抛物线 于点 .点 ,点N是 第一象限内一动点, 交 于Q点, 轴分别交 、 于S、R,试探究 与 之间的数量关系.
(1)、求抛物线L的解析式;(2)、如图1,点P在y轴上,连接 ,若 ,求点P的坐标;(3)、如图2,将抛物线L平移,使其顶点是坐标原点O,得到抛物线 ,平移直线 经过原点O,交抛物线 于点 .点 ,点N是 第一象限内一动点, 交 于Q点, 轴分别交 、 于S、R,试探究 与 之间的数量关系.