湖北省武汉市江岸区2020年数学中考二模试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
1. 2020的相反数是( )A、 2020 B、﹣2020 C、 D、2. 若代数式 在实数范围内有意义,则x的取值范围是( )A、 且 B、 C、 D、3. 下列事件不属于随机事件的是( )A、品学兼优的小涛在考试中取得满分 B、太阳从西边升起 C、掷一枚骰子得到的点数为6 D、小王在抽奖活动中获得一等奖4. 下列图形中,是中心对称图形的是( )
①菱形②等边三角形③圆④梯形⑤正方形
A、②④⑤ B、①②③⑤ C、①③⑤ D、②③⑤5. 如图所示的几何体的俯视图是( )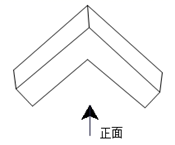 A、
A、 B、
B、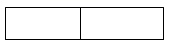 C、
C、 D、
D、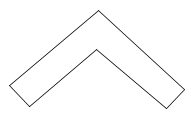 6. 在反比例函数 图象的每一支上,y都随x的增大而增大,则k的取值范围是( )A、 B、 C、 D、7. 小鲲在上学的路上有三个红绿灯,在畅通无阻的时候需要步行8分钟,闪红灯和绿灯的时间各占一半(不闪黄灯),遇到红灯的时候需要停顿1分钟,小明在10分钟内(包括10分钟)到达学校的概率为( )A、 B、 C、0 D、8. A将军和B将军要在甲地秘密集合,他们从不同地方出发相向而行.由于甲地地处密林而路况复杂,因此有一联络员在两人间不停地骑车往返来通风报信.在某一次遇见B时,B刚好抵达了甲地,联络员就骑车去接A.已知 到甲地的距离相同,且C在一开始( 时)是从B将军处向A将军处骑去.此过程中A的行进距离y(单位:m)随时间x(单位:s)的函数图象如图所示.若点D对应B到达,且B到达的时间恰为计划时间,则A迟到了( )
6. 在反比例函数 图象的每一支上,y都随x的增大而增大,则k的取值范围是( )A、 B、 C、 D、7. 小鲲在上学的路上有三个红绿灯,在畅通无阻的时候需要步行8分钟,闪红灯和绿灯的时间各占一半(不闪黄灯),遇到红灯的时候需要停顿1分钟,小明在10分钟内(包括10分钟)到达学校的概率为( )A、 B、 C、0 D、8. A将军和B将军要在甲地秘密集合,他们从不同地方出发相向而行.由于甲地地处密林而路况复杂,因此有一联络员在两人间不停地骑车往返来通风报信.在某一次遇见B时,B刚好抵达了甲地,联络员就骑车去接A.已知 到甲地的距离相同,且C在一开始( 时)是从B将军处向A将军处骑去.此过程中A的行进距离y(单位:m)随时间x(单位:s)的函数图象如图所示.若点D对应B到达,且B到达的时间恰为计划时间,则A迟到了( )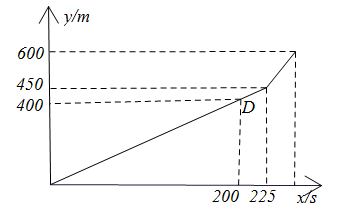 A、 B、 C、 D、9. 如图, 为⊙O的内接四边形,且 平分 , 与⊙O相切.若 ,则 ( )
A、 B、 C、 D、9. 如图, 为⊙O的内接四边形,且 平分 , 与⊙O相切.若 ,则 ( ) A、 B、 C、 D、10. (问题背景)“整体替换法”是数学里的一种常用计算方法.利用式子的特征进行整体代换,往往能解决许多看似复杂的问题.
A、 B、 C、 D、10. (问题背景)“整体替换法”是数学里的一种常用计算方法.利用式子的特征进行整体代换,往往能解决许多看似复杂的问题.(迁移运用)计算 的值
解:设原式 ,则可分析得:
根据上述方程解得: ,
而原式 ,故:原式
(联系拓展) ___________
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 某质量检测实验室统一采购了一批 芯片共16件,收集尺寸如下表:
尺寸/
195
205
220
225
275
315
数量/件
2
2
1
3
3
5
这组数据的中位数是.
13. 计算: .14. 在四边形 中, 且 , , , ,则 .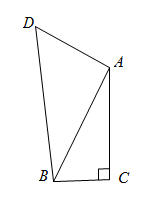 15. 如图,拋物线 过 ,且与 轴的交点分别为 ( 在 左侧).观察图像,选出下列选项中的正确项.
15. 如图,拋物线 过 ,且与 轴的交点分别为 ( 在 左侧).观察图像,选出下列选项中的正确项.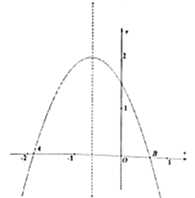
① ;② ;③ ;④若 ,则 ;⑤若抛物线 满足 且经过 ,则 与 轴必有两个不相同的交点.
16. 如图,在四边形 中, , 交 于F,使得 且 .若在线段 上取一点G,满足: 平分 且 ,则 的值为.
三、解答题
-
17. 计算: .18. 如图,矩形 在四边形 中,且满足 .
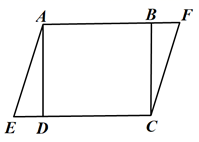
求证:四边形 为平行四边形.
19. 在武汉人民的共同努力下,疫情防控态势稳步向好,学生们分批回到了向往已久的校园.为了有序地分类开展体育活动,体育老师在全年级针对大家的兴趣爱好进行了抽样调查,并以收集的结果绘制出了以下两幅不完整的规范统计图.其中A代表跑步,B代表俯卧撑,C代表蹦跳,D代表跳绳,E代表其他类别.根据以上信息,回答下列问题:
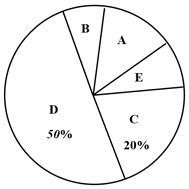 (1)、此次共有人接受调查;最受欢迎的运动是.(2)、若图中的圆半径为2,则扇形统计图中 组所对应的弧长为.(3)、若该校共有1200名学生,请估计该校喜欢蹦跳的学生共有多少.20. 如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫格点,仅用无刻度直尺,在给定网格 中画图,完成下列问题.
(1)、此次共有人接受调查;最受欢迎的运动是.(2)、若图中的圆半径为2,则扇形统计图中 组所对应的弧长为.(3)、若该校共有1200名学生,请估计该校喜欢蹦跳的学生共有多少.20. 如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫格点,仅用无刻度直尺,在给定网格 中画图,完成下列问题.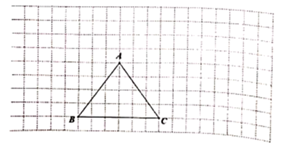 (1)、①过点B作直线 直线 ;
(1)、①过点B作直线 直线 ;
②作线段 中点R;
③作点B关于直线 的对称点 ;(2)、根据以上提示,点M、N、P分别为边 、 、 上的动点,当 的周长最小时,作出点M、N、P,并直接写出 的周长为.21. 如图,⊙ 过 的顶点A、B,交 于D,连接 、 、 , .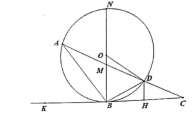 (1)、证明: 为⊙ 的切线;(2)、 平分 交 于 , 且 分别交 、⊙ 于M、N.已知 , ,求 的值.22. 某品牌 恤现在已经火遍全武汉.有一家商店正在火热售卖该T恤,每日销售量y(件)与销售单价x(元/件)之间存在一次函数关系,如下表所示.已知该T恤的成本为30元/件.
(1)、证明: 为⊙ 的切线;(2)、 平分 交 于 , 且 分别交 、⊙ 于M、N.已知 , ,求 的值.22. 某品牌 恤现在已经火遍全武汉.有一家商店正在火热售卖该T恤,每日销售量y(件)与销售单价x(元/件)之间存在一次函数关系,如下表所示.已知该T恤的成本为30元/件.销售单价x(元/件)
40
50
60
销售量y(件)
220
200
180
(1)、直接写出y与x的函数关系式(不要求写出自变量 的取值范围)(2)、当销售单价为元时,每日销售利润最大.此时最大利润为.(直接写出答案)(3)、该品牌总经理为了给武汉各店送福利,将该T恤的成本降低了m元( ).同时,应市场要求,每日销售量不得超过100件,此时每日最大销售利润为7600元.求m的值.23. 平行四边形 中,N为线段 上一动点.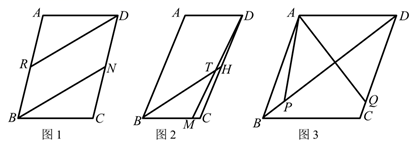 (1)、如图1,已知 .若 ,求证:四边形 为平行四边形;(2)、如图2,已知 .若 为 的角平分线,T为线段 上一点, 的延长线交线段 于点M,满足: 且 .请认真思考(1)中图形,探究 的值.(3)、如图3,平行四边形 中, , ,P在线段 上,Q在线段 上,满足: .直接写出 的最小值为.24. 如图1,抛物线 交 轴于 .
(1)、如图1,已知 .若 ,求证:四边形 为平行四边形;(2)、如图2,已知 .若 为 的角平分线,T为线段 上一点, 的延长线交线段 于点M,满足: 且 .请认真思考(1)中图形,探究 的值.(3)、如图3,平行四边形 中, , ,P在线段 上,Q在线段 上,满足: .直接写出 的最小值为.24. 如图1,抛物线 交 轴于 . (1)、直接写出抛物线 的解析式.(2)、如图1,x轴上两动点 满足: .若 (B在C左侧)为线段 上的两个动点,且满足:B点和C点关于直线 对称.过B作 轴交 于 ,过C作 轴交 于 ,连接 .求 的最大值(用含n的代数式表示).(3)、如图2,将抛物线 向下平移 个单位长度得到抛物线 . 对称轴左侧的抛物线上有一点M,其横坐标为m.以 为直径作 ,记⊙ 的最高点为Q.若Q在直线 上,求m的值.
(1)、直接写出抛物线 的解析式.(2)、如图1,x轴上两动点 满足: .若 (B在C左侧)为线段 上的两个动点,且满足:B点和C点关于直线 对称.过B作 轴交 于 ,过C作 轴交 于 ,连接 .求 的最大值(用含n的代数式表示).(3)、如图2,将抛物线 向下平移 个单位长度得到抛物线 . 对称轴左侧的抛物线上有一点M,其横坐标为m.以 为直径作 ,记⊙ 的最高点为Q.若Q在直线 上,求m的值.