湖北省黄石市阳新县2020年数学中考模拟试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
1. 2020的相反数是( )A、 2020 B、﹣2020 C、 D、2. 下面的四个汉字可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一个立体图形的三视图如图所示,则这个立体图形是( )
3. 一个立体图形的三视图如图所示,则这个立体图形是( )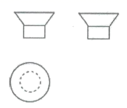 A、
A、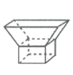 B、
B、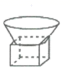 C、
C、 D、
D、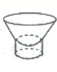 4. 下列计算正确的是( )A、 B、 C、 D、5. 二次根式 ,则a的取值范围是( )A、a≤2 B、a≤﹣2 C、a>2 D、a<06. 解不等式组 时,不等式①②的解集在同一条数轴上表示正确的是( )A、
4. 下列计算正确的是( )A、 B、 C、 D、5. 二次根式 ,则a的取值范围是( )A、a≤2 B、a≤﹣2 C、a>2 D、a<06. 解不等式组 时,不等式①②的解集在同一条数轴上表示正确的是( )A、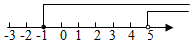 B、
B、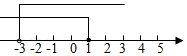 C、
C、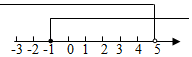 D、
D、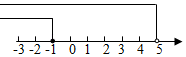 7. 如图,在平面直角坐标系中, 的顶点 在第一象限,点 、 的坐标分别为 、 , , ,直线 交 轴于点 ,若 与 关于点 成中心对称,则点 的坐标为( )
7. 如图,在平面直角坐标系中, 的顶点 在第一象限,点 、 的坐标分别为 、 , , ,直线 交 轴于点 ,若 与 关于点 成中心对称,则点 的坐标为( )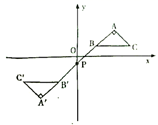 A、 B、 C、 D、8. 如图,两个全等的矩形 ,矩形 如图所示放置. 所在直线与 分别交于点 .若 .则线段 的长度是( )
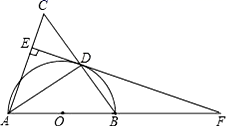
A、 B、 C、 D、8. 如图,两个全等的矩形 ,矩形 如图所示放置. 所在直线与 分别交于点 .若 .则线段 的长度是( )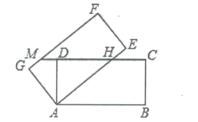 A、 B、 C、 D、29. 如图,四边形 内接于半圆O, 为直径, ,则弦 的长为( )
A、 B、 C、 D、29. 如图,四边形 内接于半圆O, 为直径, ,则弦 的长为( )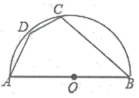 A、3.5 B、 C、 D、10. 对于一个函数,自变量x取a时,函数值y也等于a , 我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2 , 且x1<1<x2 , 则c的取值范围是( )A、c<﹣3 B、c<﹣2 C、c< D、c<1
A、3.5 B、 C、 D、10. 对于一个函数,自变量x取a时,函数值y也等于a , 我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2 , 且x1<1<x2 , 则c的取值范围是( )A、c<﹣3 B、c<﹣2 C、c< D、c<1二、填空题
-
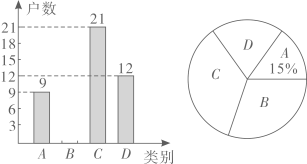
11. 计算: .12. 因式分解: .13. 根据资料显示,新冠病毒的直径约为100nm,其中1nm=1 m,则100nm用科学记数法可表示为m.14. 董永社区在创建全国卫生城市的活动中,随机检查了本社区部分住户五月份某周内“垃圾分类”的实施情况,将他们绘制了两幅不完整的统计图( .小于5天; .5天; .6天; .7天),则扇形统计图 部分所对应的圆心角的度数是.
 15. 如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=°.
15. 如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=°.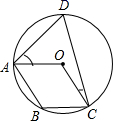 16. 设 是一列正整数,其中 表示第一个数, 表示第二个数,依此类推, 表示第 个数( 是正整数),已知 ,则 等于.
16. 设 是一列正整数,其中 表示第一个数, 表示第二个数,依此类推, 表示第 个数( 是正整数),已知 ,则 等于.三、解答题
-
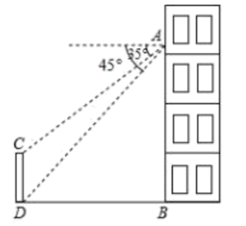
17. 先化简,再求值: ÷( ﹣m﹣1),其中m=6.18. 如图,在一场马拉松比赛中,某人在大楼 处,测得起点拱门 的顶部 的俯角为 ,底部 的俯角为 ,如果 处离地面的高度 米,求起点拱门 的高度,(结果精确到; ,参考数据: )
 19. 如图,菱形 中,作 、 ,分别交 、 的延长线于点 .
19. 如图,菱形 中,作 、 ,分别交 、 的延长线于点 .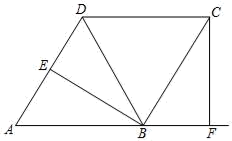 (1)、求证: ;(2)、若点 恰好是 的中点, ,求 的值.20. 如图,一次函数 的图象与反比例函数 的图象交于点 和点C,与y轴交于点B, 的面积是6.
(1)、求证: ;(2)、若点 恰好是 的中点, ,求 的值.20. 如图,一次函数 的图象与反比例函数 的图象交于点 和点C,与y轴交于点B, 的面积是6.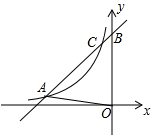 (1)、求一次函数与反比例函数的表达式;(2)、当 时,比较 与 的大小.21. 已知x1 , x2是一元二次方程x2﹣x+m﹣2=0的两个实根.(1)、求m的取值范围;(2)、若m满足2x1+x2=m+1,求m的值.22. “十一”期间,老张在某商场购物后,参加了出口处的抽奖活动.抽奖规则如下:每张发票可摸球一次,每次从装有大小形状都相同的1个白球和2个红球的盒子中,随机摸出一个球,若摸出的是白球,则获得一份奖品;若摸出的是红球,则不获奖.(1)、求每次摸球中奖的概率;(2)、老张想“我手中有两张发票,那么中奖的概率就翻了一倍.”你认为老张的想法正确吗?用列表法或画树形图分析说明.23. 某工程队(有甲、乙两组)承包一条路段的修建工程,要求在规定时间内完成.(1)、已知甲组单独完成这项工作所需时间比规定时间多32天,乙组单独完成这项工程所需时间比规定时间多12,如果甲、乙两组先合作20天,剩下的由甲组单独做,则要误期2天完成,那么规定时间是多少天?(2)、在实际工作中,甲、乙两组合做这项工作的 后,工程队又承包了其他路段的工程,需抽调一组过去,从按时完成任务的角度考虑,你认为留下哪一组最好?请说明理由.
(1)、求一次函数与反比例函数的表达式;(2)、当 时,比较 与 的大小.21. 已知x1 , x2是一元二次方程x2﹣x+m﹣2=0的两个实根.(1)、求m的取值范围;(2)、若m满足2x1+x2=m+1,求m的值.22. “十一”期间,老张在某商场购物后,参加了出口处的抽奖活动.抽奖规则如下:每张发票可摸球一次,每次从装有大小形状都相同的1个白球和2个红球的盒子中,随机摸出一个球,若摸出的是白球,则获得一份奖品;若摸出的是红球,则不获奖.(1)、求每次摸球中奖的概率;(2)、老张想“我手中有两张发票,那么中奖的概率就翻了一倍.”你认为老张的想法正确吗?用列表法或画树形图分析说明.23. 某工程队(有甲、乙两组)承包一条路段的修建工程,要求在规定时间内完成.(1)、已知甲组单独完成这项工作所需时间比规定时间多32天,乙组单独完成这项工程所需时间比规定时间多12,如果甲、乙两组先合作20天,剩下的由甲组单独做,则要误期2天完成,那么规定时间是多少天?(2)、在实际工作中,甲、乙两组合做这项工作的 后,工程队又承包了其他路段的工程,需抽调一组过去,从按时完成任务的角度考虑,你认为留下哪一组最好?请说明理由.