河南省南阳市卧龙区2020年数学中考一模试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
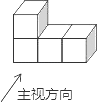
1. 的绝对值是( )A、 B、 C、 D、2. 预计到2025年,中国5G用户将达到460000000.将460000000科学记数法表示成a×10n(1≤a<10,n是整数)的形式,则n的值应为( )A、9 B、8 C、7 D、63. 如图,由四个正方体组成的几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列计算:① ;②(x﹣2y)2=x2﹣4y2;③(﹣a)4•a3=﹣a7;④x10÷x5=x2 , 其中错误的个数是( )A、1 B、2 C、3 D、45. 给定一组数据,那么这组数据的( )可以有多个.A、平均数 B、中位数 C、方差 D、众数6. 不等式组 的解集在数轴上表示正确的是( )A、
4. 下列计算:① ;②(x﹣2y)2=x2﹣4y2;③(﹣a)4•a3=﹣a7;④x10÷x5=x2 , 其中错误的个数是( )A、1 B、2 C、3 D、45. 给定一组数据,那么这组数据的( )可以有多个.A、平均数 B、中位数 C、方差 D、众数6. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、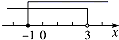 C、
C、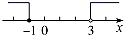 D、
D、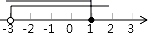 7. 若关于x的一元二次方程x2+4x+k=0有两个不相等的实数根,则k的取值范围是( )A、k<4 B、k>4 C、k<1 D、k>18. 学校决定从甲、乙、丙三名学生中随机抽取两名介绍学习经验,则同时抽到乙、丙两名同学的概率为( )A、 B、 C、 D、9. 如图,已知∠1=39°,∠2=39°,∠3=54°,则∠4的度数是( )
7. 若关于x的一元二次方程x2+4x+k=0有两个不相等的实数根,则k的取值范围是( )A、k<4 B、k>4 C、k<1 D、k>18. 学校决定从甲、乙、丙三名学生中随机抽取两名介绍学习经验,则同时抽到乙、丙两名同学的概率为( )A、 B、 C、 D、9. 如图,已知∠1=39°,∠2=39°,∠3=54°,则∠4的度数是( ) A、39° B、51° C、54° D、126°10. 如图,已知点A1(1,1),将点A1向上平移1个单位长度,再向右平移2个单位长度得到点A2;将点A2向上平移2个单位长度,再向右平移4个单位长度得到点A3;将点A3向上平移4个单位长度,再向右平移8个单位长度得到点A4 , …按这个规律平移下去得到点An(n为正整数),则点An的坐标是( )
A、39° B、51° C、54° D、126°10. 如图,已知点A1(1,1),将点A1向上平移1个单位长度,再向右平移2个单位长度得到点A2;将点A2向上平移2个单位长度,再向右平移4个单位长度得到点A3;将点A3向上平移4个单位长度,再向右平移8个单位长度得到点A4 , …按这个规律平移下去得到点An(n为正整数),则点An的坐标是( ) A、(2n , 2n﹣1) B、(2n﹣1 , 2n) C、(2n﹣1 , 2n+1) D、(2n﹣1,2n﹣1)
A、(2n , 2n﹣1) B、(2n﹣1 , 2n) C、(2n﹣1 , 2n+1) D、(2n﹣1,2n﹣1)二、填空题
-
11. 计算:( ﹣1)0﹣( )﹣1=.12. 已知抛物线y=x2+mx+9的顶点在x轴上,则m的值为.13. 如图,直线y=- x+4与 x轴、y轴的交点为A,B.按以下步骤作图:
①以点 A 为圆心,适当长度为半径作弧,分别交 AB,x 轴于点 C,D;
②分别以点 C,D 为圆心,大于 CD的长为半径作弧,两弧在∠OAB内交于点M;③作射线AM,交 y 轴于点E.则点 E 的坐标为
 14. 如图,在扇形AOB中,∠AOB=90°,点C在 , ,OA=3,CD⊥OB于点D,则图中阴影部分的面积为.
14. 如图,在扇形AOB中,∠AOB=90°,点C在 , ,OA=3,CD⊥OB于点D,则图中阴影部分的面积为. 15. 如图,在边长为3的等边△ABC中,点D在AC上,且CD=1,点E在AB上(不与点A、B重合),连接DE,把△ADE沿DE折叠,当点A的对应点F落在等边△ABC的边上时,AE的长为.
15. 如图,在边长为3的等边△ABC中,点D在AC上,且CD=1,点E在AB上(不与点A、B重合),连接DE,把△ADE沿DE折叠,当点A的对应点F落在等边△ABC的边上时,AE的长为.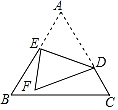
三、解答题
-
16. 先化简,再求值:( ﹣2)÷ ,其中x= ﹣1.17. 某学校为了解九年级男同学1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制了不完整的成绩等级频数表和扇形统计图.
成绩等级
频数
A
24
B
10
C
b
D
2
合计
a
 (1)、表中a= , b=;(2)、扇形图中C的圆心角度数是;(3)、若该校共有九年级男生600人,请估计没有获得A等级的学生人数.18. 已知△ABC内接于⊙O,AB是⊙O的直径,OD∥AC,AD=OC.
(1)、表中a= , b=;(2)、扇形图中C的圆心角度数是;(3)、若该校共有九年级男生600人,请估计没有获得A等级的学生人数.18. 已知△ABC内接于⊙O,AB是⊙O的直径,OD∥AC,AD=OC. (1)、求证:四边形OCAD是平行四边形;(2)、若AD与⊙O相切,求∠B.19. 如图,某海监船向正西方向航行,在A处望见一艘正在作业的渔船D在南偏西45°方向,海监船航行到B处时,望见渔船D在南偏东45°方向,又航行半小时到达C处望见渔船D在南偏东62°方向,若海监船的速度为40海里/小时,求A、B之间的距离.(精确到0.1海里,参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
(1)、求证:四边形OCAD是平行四边形;(2)、若AD与⊙O相切,求∠B.19. 如图,某海监船向正西方向航行,在A处望见一艘正在作业的渔船D在南偏西45°方向,海监船航行到B处时,望见渔船D在南偏东45°方向,又航行半小时到达C处望见渔船D在南偏东62°方向,若海监船的速度为40海里/小时,求A、B之间的距离.(精确到0.1海里,参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88) 20. 某兴趣小组对函数y= 的图象和性质进行探究,请你帮助解决下面问题:(1)、函数y= 中自变量x的取值范围是;(2)、如表是x、y的几组对应值,则m=;
20. 某兴趣小组对函数y= 的图象和性质进行探究,请你帮助解决下面问题:(1)、函数y= 中自变量x的取值范围是;(2)、如表是x、y的几组对应值,则m=;x
…
﹣2
﹣1
0
1
2
4
5
6
7
8
…
y
…
m
0
﹣1
3
2
…
(3)、如图,已经画出了该函数图象的一部分,请你画出函数图象的另一部分; (4)、该函数图象两个分支关于一个点成中心对称,这个点的坐标是;(5)、若函数y= 的图象上有三点A(x1 , y1)、B(x2 , y2)、C(x3 , y3)且x1<x2<3<x3 , 则y1、y2、y3的大小关系是(用“<”连接).21. 在2020年新冠肺炎疫情期间,我市某企业为支援湖北,准备将购买的70吨蔬菜运往武汉,现有甲、乙两种货车可以租用,已知2辆甲货车和3辆乙货车一次可运44吨蔬菜;3辆甲货车和1辆乙货车一次可运38吨蔬菜.(1)、求每辆甲种货车和每辆乙种货车一次分别能运多少吨蔬菜?(2)、已知甲种货车每辆租金500元,乙种货车每辆租金450元,该企业共租用甲、乙两种货车8辆,设租甲种货车a辆,求租车总费用w(元)与a之间的函数关系式,并求出自变量a的取值范围;(3)、在(2)的条件下,请你为该企业设计出费用最少的方案,并求出最少的租车费用.22. 在△ABC中,AC=BC,∠ACB=α,点D为直线BC上一动点,过点D作DF∥AC交直线AB于点F,将AD绕点D顺时针旋转α得到ED,ED交直线AB于点O,连接BE.
(4)、该函数图象两个分支关于一个点成中心对称,这个点的坐标是;(5)、若函数y= 的图象上有三点A(x1 , y1)、B(x2 , y2)、C(x3 , y3)且x1<x2<3<x3 , 则y1、y2、y3的大小关系是(用“<”连接).21. 在2020年新冠肺炎疫情期间,我市某企业为支援湖北,准备将购买的70吨蔬菜运往武汉,现有甲、乙两种货车可以租用,已知2辆甲货车和3辆乙货车一次可运44吨蔬菜;3辆甲货车和1辆乙货车一次可运38吨蔬菜.(1)、求每辆甲种货车和每辆乙种货车一次分别能运多少吨蔬菜?(2)、已知甲种货车每辆租金500元,乙种货车每辆租金450元,该企业共租用甲、乙两种货车8辆,设租甲种货车a辆,求租车总费用w(元)与a之间的函数关系式,并求出自变量a的取值范围;(3)、在(2)的条件下,请你为该企业设计出费用最少的方案,并求出最少的租车费用.22. 在△ABC中,AC=BC,∠ACB=α,点D为直线BC上一动点,过点D作DF∥AC交直线AB于点F,将AD绕点D顺时针旋转α得到ED,ED交直线AB于点O,连接BE. (1)、问题发现:
(1)、问题发现:如图1,α=90°,点D在边BC上,猜想:
①AF与BE的数量关系是
②∠ABE=度.
(2)、拓展探究:如图2,0°<α<90°,点D在边BC上,请判断AF与BE的数量关系及∠ABE的度数,并给予证明.
(3)、解决问题如图3,90°<α<180°,点D在射线BC上,且BD=3CD,若AB=8,请直接写出BE的长.
23. 如图,抛物线y=ax2+bx+c(a<0)与x轴交于点A(﹣2,0)、B(4,0),与y轴交于点C,且OC=2OA. (1)、该抛物线的解析式为;(2)、直线y=kx+l(k>0)与y轴交于点D,与直线BC交于点M,与抛物线上直线BC上方部分交于点P,设m= ,求m的最大值及此时点P的坐标;(3)、若点D、P为(2)中求出的点,点Q为x轴的一个动点,点N为坐标平面内一点,当以点P、D、Q、N为顶点的四边形为矩形时,直接写出点N的坐标.
(1)、该抛物线的解析式为;(2)、直线y=kx+l(k>0)与y轴交于点D,与直线BC交于点M,与抛物线上直线BC上方部分交于点P,设m= ,求m的最大值及此时点P的坐标;(3)、若点D、P为(2)中求出的点,点Q为x轴的一个动点,点N为坐标平面内一点,当以点P、D、Q、N为顶点的四边形为矩形时,直接写出点N的坐标.