河南南阳市卧龙区2020年数学中考二模试卷

试卷更新日期：2020-08-10 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各数中最大的负数是（）

A、 $- \frac{1}{3}$ B、 $- \frac{1}{2}$ C、－1 D、－3

查看试题解析
2. 某种计算机完成一次基本运算的时间约为1 纳秒（ns），已知1 纳秒＝0.000000001秒，该计算机完成15次基本运算，所用时间用科学记数法表示为（）

A、1.5× $10^{- 9}$ 秒 B、15× $10^{- 9}$ 秒 C、1.5× $10^{- 8}$ 秒 D、15× $10^{- 8}$ 秒

查看试题解析
3. 如图， $C D // A B$ ，点O在 $A B$ 上， $O E$ 平分 $∠ B O D$ ， $O F ⊥ O E$ ， $∠ D = 110 °$ ，则 $∠ A O F =$ （）

A、 $25 °$ B、 $30 °$ C、 $35 °$ D、 $40 °$

查看试题解析
4. 小明同学做了下面四道计算题：① ${(x^{2})}^{3} = x^{5}$ ；② ${(- x - y)}^{2} = x^{2} - 2 x y + y^{2}$ ；③ $(x + y) (y - x) = y^{2} - x^{2}$ ；④ ${(\frac{1}{3} x^{2} y)}^{3} = \frac{1}{9} x^{6} y^{3}$ ，其中正确的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
5. 关于x的一元二次方程 $x^{2} - m x + m - 2 = 0$ 的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、m不确定，所以无法判断

查看试题解析
6. 一个几何体由一些大小相同的小正方体组成，如图是它的主视图和左视图，那么组成该几何体所需小正方体的个数最少为（）

A、5 B、6 C、7 D、8

查看试题解析
7. 如果一组数据6、7、x、9、5的平均数是2x，那么这组数据的方差为（）

A、4 B、3 C、2 D、1

查看试题解析
8. 如图，在 $R t Δ A B C$ 中， $∠ B = 90^{\circ}$ ，以点 $A$ 为圆心，适当长为半径画弧，分别交 $A B 、 A C$ 于点 $D ， E$ ，再分别以点 $D 、 E$ 为圆心，大于 $\frac{1}{2} D E$ 为半径画弧，两弧交于点 $F$ ，作射线 $A F$ 交边 $B C$ 于点 $B G = 1 ， A C = 4$ ，则 $Δ A C G$ 的面积是（）

A、 $1$ B、 $\frac{3}{2}$ C、 $2$ D、 $\frac{5}{2}$

查看试题解析
9. 如图1，已知在四边形ABCD中， $A B / / C D$ ， $∠ B = 90 °$ ， $A C = A D$ ，动点P从点B出发沿折线B→A→D→C的方向以1个单位/秒的速度匀速运动，整个运动过程中，△BCP的面积S与运动时间t（秒）的函数关系如图2所示，则AD的长为（）

A、5 B、 $\sqrt{34}$ C、8 D、 $2 \sqrt{3}$

查看试题解析
10. 我们知道，四边形具有不稳定性，如图，平行四边形ABCD的顶点A在y轴上， $A B / / x$ 轴，已知点B(4，3)，D(2，6)，固定A、B两点，拖动CD边向右下方平行移动，使平行四边形ABCD的面积变为原来的 $\frac{1}{3}$ ，则变换后点D的对应点 $D^{'}$ 的坐标为（）

A、 $(2 \sqrt{3} ， 3)$ B、 $(2 \sqrt{3} ， 6)$ C、 $(\sqrt{3} ， 4)$ D、 $(2 \sqrt{3} ， 4)$

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{- 8} + {(\frac{1}{2})}^{- 2} - π^{0} =$ .

查看试题解析
12. 婷婷和她妈妈玩猜拳游戏.规定每人每次至少要出一个手指，两人出拳的手指数之和为偶数时婷婷获胜.那么，婷婷获胜的概率为.

查看试题解析
13. 如图，在△ABC中， $∠ B A C = 90 °$ ， $∠ B = 36 °$ ，AD是BC边上的中线，将△ACD沿AD折叠，使点C落在点F处，DF交AB于点E，则∠DEB＝.

查看试题解析
14. 如图，已知在矩形ABCD中， $A B = 4$ ，以点A为圆心，AD长为半径作弧 $\overset{⌢}{D E}$ ，交AB于点E，以AB为直径的半圆恰好与边DC相切，则图中阴影部分的面积为.

查看试题解析
15. 如图，已知在△ABC中， $∠ A C B = 90 °$ ， $A C = 2$ ， $B C = 4$ ，点E为AB的中点，D为BC边上的一动点，把△ACD沿AD折叠，点C落在点F处，当△AEF为直角三角形时，CD的长为.

查看试题解析

三、解答题

16. 先化简，再求值： $(\frac{3}{a + 1} - a + 1) \div \frac{a^{2} - 4 a + 4}{a + 1}$ ，其中a的值从不等式组 $- \sqrt{2} < a < \sqrt{5}$ 的解集中选取一个整数.

查看试题解析
17. 某学校为了解九年级的600名学生每天的自主学习情况，随机抽查了九年级的部分学生，并调查他们每天自主学习的时间.根据调查结果，制作了两副不完整的统计图（图1图2），请根据统计图中的信息回答下列问题：

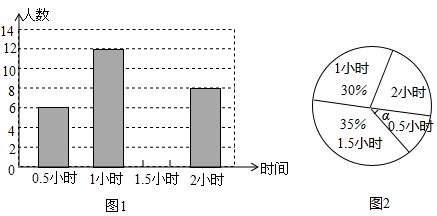(1)、本次调查的学生人数是人；

(2)、图2中角 $α$ 是度；

(3)、将图1条形统计图补充完整；

(4)、估算该校九年级学生自主学习不少于1.5小时有多少人.

查看试题解析
18. 如图，已知在Rt△ABC中， $∠ A C B = 90 °$ ，以BC为直径作 $⊙ O$ 交AB于点E，D为AC边的中点，连接OD、DE，

(1)、求证：DE是 $⊙ O$ 的切线.

(2)、填空：①若 $A C = 3$ ， $A E = 1$ ，则 $⊙ O$ 的半径长是.
②当∠A＝时，四边形OCDE是正方形.

查看试题解析
19. 为积极宣传国家相关政策，某村在一山坡的顶端的平地上竖立一块宣传牌 $A B$ .小明为测得宣传牌的高度，他站在山脚C处测得宣传牌的顶端 $A$ 的仰角为 $40 °$ ，已知山坡 $C D$ 的坡度 $i = 1 ： 2$ ，山坡 $C D$ 的长度为 $4 \sqrt{5}$ 米，山坡顶端 $D$ 与宣传牌底端 $B$ 的水平距离为2米，求宣传牌的高度 $A B$ （精确到1米）
（参考数据： $s i n 40 ° \approx 0.64$ ， $c o s 40 ° \approx 0.77$ ， $t a n 40 ° \approx 0.84$ ， $\sqrt{5} \approx 2.24$ ）

查看试题解析
20. 某茶具店购进了A、B两种不同的茶具，1套A种茶具和2套B种茶具共需250元；3套A种茶具和4套B种茶具共需600元.

(1)、求A、B两种茶具每套的进价分别是多少元？

(2)、由于茶具畅销，茶具店准备再购进A、B两种茶具共80套，但这次进货时，工厂对A种茶具每套进价提高了8%，而B种茶具每套按第一次进价的八折，若茶具店本次进货总钱数不超过6240元，则最多可进A种茶具几套？

(3)、若销售一套A种茶具可获利30元，销售一套B种茶其可获利20元，在（2）的条件下，如何进货可使本次购进茶具获利最多？最多是多少？

查看试题解析
21. 如图，点 $A (\frac{3}{2} ， 4)$ 、 $B (m ， 2)$ 是直线 $A B ： y = k x + b$ 与反比例函数 $y = \frac{n}{x} (x > 0)$ 图象的两个交点， $A C ⊥ x$ 轴于点C，已知点D（0，1），连接AD、BD、BC，

(1)、求反比例函数和直线AB的表达式；

(2)、根据函数图象直接写出当 $x > 0$ 时不等式 $k x + b > \frac{n}{x}$ 的解集；

(3)、设△ABC和△ABD的面积分别为 $S_{1}$ 、 $S_{2}$ ，求 $S_{2} - S_{1}$ 的值.

查看试题解析
22. 如图1，在矩形ABCD中，AB＝6，BC＝8，点E是边CD上的点，且CE＝4，过点E作CD的垂线，并在垂线上截取EF＝3，连接CF.将△CEF绕点C按顺时针方向旋转，记旋转角为a.

(1)、问题发现
当a＝0°时，AF＝， BE＝， $\frac{A F}{B E}$ ＝；

(2)、拓展探究
试判断：当0°≤a°＜360°时， $\frac{A F}{B E}$ 的大小有无变化？请仅就图2的情况给出证明.

(3)、问题解决
当△CEF旋转至A，E，F三点共线时，直接写出线段BE的长.

查看试题解析
23. 如图，抛物线 $y = a x^{2} + b x - 2$ 经过点A(4，0)、B(1，0)，交y轴于点C.

(1)、求抛物线的解析式.

(2)、点P是直线AC上方的抛物线上一点，过点P作 $P H ⊥ A C$ 于点H，求线段PH长度的最大值.

(3)、Q为抛物线上的一个动点（不与点A、B、C重合）， $Q M ⊥ x$ 轴于点M，是否存在点Q，使得以点A、Q、M三点为顶点的三角形与△AOC相似？若存在，直接写出点Q的坐标，若不存在，请说明理由.

查看试题解析