海南省定安县2020年数学中考二模试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
1. 如果向西走30米记作-30米,那么向东走20米记作( )A、-20米 B、+20米 C、-10米 D、+50米2. 下列运算中,正确的是( )A、 B、 C、 D、3. 地球上陆地的面积约为149 000 000平方千米,把数据149 000 000用科学记数法表示为 米,其中 等于( )A、6 B、7 C、8 D、94. 从不同方向看一只茶壶,你认为是俯视效果图的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 在函数y= 中,自变量x的取值范围是( )A、x≤﹣3 B、x≥﹣3 C、x<﹣3 D、x>﹣36. 在一个不透明的盒子中装有10个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为 ,则黄球的个数为( )A、4 B、5 C、6 D、77. 若一个正多边形的一个内角是144°,则这个多边形的边数为( )A、12 B、11 C、10 D、98. 如图, , 交 于 ,若 ,则 等于( )
5. 在函数y= 中,自变量x的取值范围是( )A、x≤﹣3 B、x≥﹣3 C、x<﹣3 D、x>﹣36. 在一个不透明的盒子中装有10个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为 ,则黄球的个数为( )A、4 B、5 C、6 D、77. 若一个正多边形的一个内角是144°,则这个多边形的边数为( )A、12 B、11 C、10 D、98. 如图, , 交 于 ,若 ,则 等于( )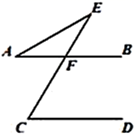 A、30° B、45° C、60° D、120°9. 如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于( )
A、30° B、45° C、60° D、120°9. 如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于( )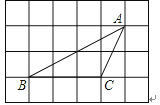 A、 B、 C、 D、10. 已知:如图,在△ABC中,∠ADE=∠C,则下列等式成立的是 ( )
A、 B、 C、 D、10. 已知:如图,在△ABC中,∠ADE=∠C,则下列等式成立的是 ( )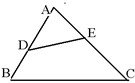 A、 B、 C、 D、11. 如图,直线l与x轴、y轴分别交于A、B两点,与反比例函数y= 的图象在第一象限相交于点C.若AB=BC,△AOB的面积为3,则k的值为( )
A、 B、 C、 D、11. 如图,直线l与x轴、y轴分别交于A、B两点,与反比例函数y= 的图象在第一象限相交于点C.若AB=BC,△AOB的面积为3,则k的值为( ) A、6 B、9 C、12 D、1812. 如图,在矩形 中, , , ,则 内切圆的半径是( )
A、6 B、9 C、12 D、1812. 如图,在矩形 中, , , ,则 内切圆的半径是( )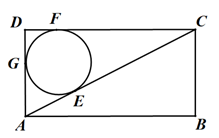 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
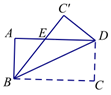
13. 分解因式: .14. 不等式组 的解集为.15. 如图,矩形 中,沿着直线 折叠,使点 落在 处, 交 于 , , ,则 的长是.
 16. 如图,在矩形 中, , ,以点 为圆心, 为半径作圆与 的延长线交于点 ,连接 ,则阴影部分的面积是 .
16. 如图,在矩形 中, , ,以点 为圆心, 为半径作圆与 的延长线交于点 ,连接 ,则阴影部分的面积是 .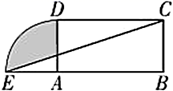
三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 定安粽子有着“海南第一粽”之美称,定安粽分为两种,用糯米制作的又称糯米粽,用籼米制作的称籼米粽.小影购买6个糯米粽和4个籼米粽,共花费100元;小慧购买3个糯米粽和5个籼米粽,共花费71元.求糯米粽和籼米粽的单价分别是多少元?19. 某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.(1)、确定调查方式时,甲同学说:“我到七年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.(2)、他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.请你根据以上图表提供的信息解答下列问题:
类别
频数(人数)
频率
武术类
0.20
书画类
15
0.15
棋牌类
25
b
器乐类
合计
a
1.00
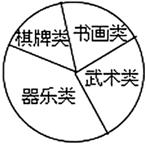
① _▲_, _▲_;②在扇形统计图中,器乐类所对应扇形的圆心角是_▲_度;
③若该校七年级有学生460人,请你估计大约有多少学生参加武术类校本课程.
20. 如图,某大楼的顶部有一块广告牌 ,小背在山坡的坡脚 处测得广告牌底部的仰角为45°,沿坡面 向上走到 处测得广告牌顶部C的仰角为30°.已知山坡 的坡度为 , 米, 米.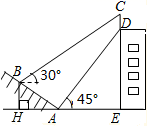
此题考查了折叠的性质、矩形的性质、全等三角形的判定与性质以及勾股定理的应用.熟练掌握折叠的性质是关键.
(1)、求点B距地面的高度 ;(2)、求广告牌 的高度.(结果保留根号)21. 如图,在正方形 中,E是边 上的动点(与点A、D不重合),且 , 于点G, 与 的延长线交于点H,连接 、 .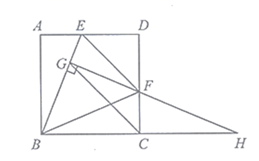 (1)、求证:① ;② ;(2)、若 ,在点E运动过程中,探究:
(1)、求证:① ;② ;(2)、若 ,在点E运动过程中,探究:①线段 的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
②当 为何值时, 为等腰直角三角形.
22. 如图,抛物线 与坐标轴交于点 ,点 和点 ,连接 .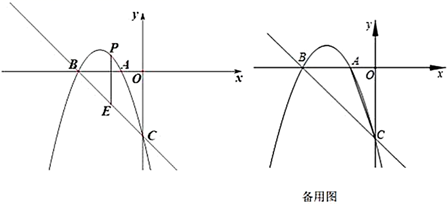 (1)、求抛物线的解析式;(2)、如图,已知点P在线段 的上方(不包括点B和点C),过P点作x轴的垂线交直线 于点E,求线段 的最大值;(3)、该抛物线上是否存在点P,使得 ?若存在,求点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图,已知点P在线段 的上方(不包括点B和点C),过P点作x轴的垂线交直线 于点E,求线段 的最大值;(3)、该抛物线上是否存在点P,使得 ?若存在,求点P的坐标;若不存在,请说明理由.