广西梧州市藤县2020年数学中考一模试卷

试卷更新日期：2020-08-10 类型：中考模拟

进入出卷网下载

一、选择题

1. 4的平方根是（）

A、 4 B、2 C、－2 D、±2

查看试题解析
2. 如图，∠1=∠2，∠3=35°，则∠4等于（）

A、120° B、130° C、145° D、150°

查看试题解析
3. 下列计算正确的是（）

A、7a﹣4a=3 B、（2a²）³=8a⁶ C、3a•（﹣2a）³=24a⁴ D、a³+2a=2a⁴

查看试题解析
4. 已知圆锥的底面半径为2cm，母线长为5cm，则圆锥的侧面积是（）

A、10 cm² B、5π cm² C、10π cm² D、16π cm²

查看试题解析
5. 若正比例函数的图象经过点(﹣4，2)，则它也经过点（）

A、(2，-1) B、(﹣1，﹣2) C、(-2，﹣1) D、(1，﹣2)

查看试题解析
6. 在平面直角坐标系中，将直线l₁：y=﹣3x﹣1平移后，得到直线l₂：y=﹣3x﹣4，则下列平移方式正确的是（）

A、将l₁向左平移1个单位 B、将l₁向右平移1个单位 C、将l₁向上平移2个单位 D、将l₁向上平移1个单位

查看试题解析
7. 如图，每个小正方形的边长为1，格点A、B、C在同一圆弧上，若点A的坐标为(﹣2，3)，则该圆弧所在圆的圆心坐标是（）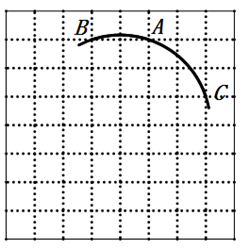

A、(﹣1，1) B、(﹣3，0) C、(﹣3，1) D、(0，1)

查看试题解析
8. 如图， $R t △ A B C$ 中，∠ACB=90°，CD⊥AB于点D，BC=6，AC=8，则sin∠1的值为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

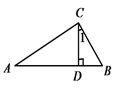查看试题解析
9. 若点O是 $△ A B C$ 的外心，且∠BOC=50°，则∠BAC的度数为（）

A、25° B、130° C、25°或130° D、25°或155°

查看试题解析
10. 若不等式组 ${\begin{array}{l} x - m < 0 \\ 1 - 2 x \leq 7 \end{array}$ 有三个非负整数解，则m的取值范围是（）

A、 $2 < m < 3$ B、 $2 < m \leq 3$ C、 $3 < m < 4$ D、 $3 < m \leq 4$

查看试题解析
11. 如图，将矩形ABCD绕点A旋转至矩形 $A B^{'} C^{'} D^{'}$ 位置，此时 $A C^{'}$ 的中点恰好与D点重合，AB'交CD于点E，若AD=3，则 $△$ AEC的面积为（）

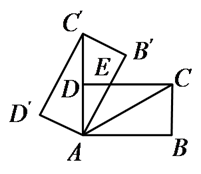A、12 B、4 $\sqrt{3}$ C、3 $\sqrt{3}$ D、6

查看试题解析
12. 若关于x的方程|ax²+bx+c|=5有三个不相等的实数根，则二次函数y=ax²+bx+c有（）

A、最小值为5 B、最大值为5 C、最大值为5或最小值-5 D、最大值-5或最小值5

查看试题解析

二、填空题

13. 分解因式：ab²+4ab+4a=.

查看试题解析
14. 从2个女生1个男生中随机抽取两名，则抽到两个女生的概率为.

查看试题解析
15. 如图，菱形ABCD的对角线AC、BD相交于点O，AB=5，AC=6，AC的平行线DE交BC的延长线于点E，则四边形ACED的面积为.

查看试题解析
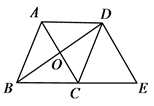16. 如图，⊙O的直径AB垂直于弦CD，垂足是E，∠A=30°，AB=4，则AE的长为.

查看试题解析
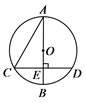17. 如图，直角坐标系xOy中，四边形ODEF和四边形ABCD都是正方形，点F在x轴的正半轴上，点C在边DE上，反比例函数 $y = \frac{k}{x}$ （k≠0，x＞0）的图象过点B，E.若AB=2，则正方形ODEF的边长为.

查看试题解析
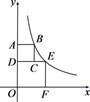18. 用同样大小的按如图所示的规律摆放，则第20个图形有枚.

查看试题解析

三、解答题

19. 计算： |﹣3|+ $\sqrt{3}$ tan30°﹣ $\sqrt{18}$ ﹣2020⁰﹣ ${(- \frac{1}{3})}^{- 2}$ .

查看试题解析
20. 先化简，再求值： $\frac{x - 2}{x - 1} \div (\frac{x^{2} - 1}{x - 1} - \frac{3}{x - 1})$ ，其中x是不等式 $x + 1 < \frac{x + 6}{2}$ 的正整数解.

查看试题解析
21. 如图，点E是平行四边形ABCD的边DC延长线上一点，连接AC、AE、BE，AE交BC于F，CE=DC，CF=EF.求证：四边形ABEC是矩形.

查看试题解析
22. 如图，BC∥AD，AB=4，∠BAD=60°，B、C、E在同一直线上，∠EAD=45°，求BE的长.

查看试题解析

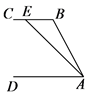23. 某校教务处李主任为了了解本校1200名学生参加安全知识网络平台学习情况，从中随机抽取部分学生的学习情况作为样本，按不合格、合格、良好、优秀四个等级记录，并将数据整理计算，得到下面的频率分布表：

等级	不合格	合格	良好	优秀
频数（人）	6	93	②	54
频率	①	0.31	0.49	0.18

(1)、学校在此次检查中一共抽查了名学生；

(2)、补充表格中所缺的两个数据：① ， ② ；

(3)、样本中的中位数落在等级内；

(4)、学校在这次检查中，良好以上（包含良好）等级的人数约有人.

查看试题解析

24. 某种植户计划将一片荒山改良后种植沃柑，经市场调查得知，当种植沃柑的面积x不超过15亩时，每亩可获得利润y=1900元；超过15亩时，每亩获得利润y（元）与种植面积x（亩）之间的函数关系：y=kx+b，并且当x=20时，y=1800；当x=25时，y=1700.

(1)、请求出y与x的函数关系式，并写出自变量的取值范围；

(2)、设种植户种植x亩沃柑所获得的总利润为w元，由于受条件限制，种植沃柑面积x不超过50亩，求该种植户种植多少亩获得的总利润最大，并求总利润w（元）的最大值.

查看试题解析
25. 如图， $△$ ABC中，∠C=90°，AC=6，AB=10，点O在BC边的中线AD上，OB 平分∠ABC，⊙O与BC相切于点E.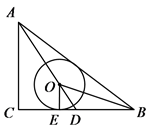

(1)、求证：AB为⊙O的切线；

(2)、求⊙O的半径；

(3)、求tan∠BAD.

查看试题解析
26. 已知抛物线y=-x²+2x+3与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，顶点为D，直线CD与x轴交于点E.

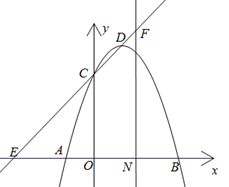(1)、求A、B的坐标；

(2)、求点E的坐标；

(3)、过线段OB的中点N作x轴的垂线并交直线CD于点F，则直线NF上是否存在点M，使得点M到直线CD的距离等于点M到原点O的距离？若存在，求出点M的坐标；若不存在，请说明理由.

查看试题解析