广西柳州市柳江区2020年数学中考模拟试卷（7月）

试卷更新日期：2020-08-10 类型：中考模拟

进入出卷网下载

一、选择题

1. 截至北京时间2020年3月22日14时30分，全球新冠肺炎确诊病例达 $305740$ 例，超过 $30$ 万，死亡病例累计 $12762$ 人，将“ $305740$ ”这个数字用科学记数法表示（）

A、 $3.0574 \times 10^{5}$ B、 $3.0574 \times 10^{4}$ C、 $3.0 \times 10^{5}$ D、 $3.1 \times 10^{5}$

查看试题解析
2. 如图，四个图标分别是剑桥大学、北京大学、浙江大学和北京理工大学的校徽的重要组成部分，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在实数-3， $\sqrt{3}$ ，0，-1中，最小的数是（）

A、-3 B、0 C、-1 D、 $\sqrt{3}$

查看试题解析
4. 不等式组 ${\begin{array}{l} x > 1 \\ x \leq 2 \end{array}$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
5. 如图是由大小相同的5个小正方体搭成的几何体，则它的主视图是（）

A、 B、 C、 D、

查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{5} + \sqrt{2} = \sqrt{7}$ B、 $7 m - 4 m = 3$ C、 $a^{5} \cdot a^{3} = a^{8}$ D、 ${(\frac{1}{3} a^{3})}^{2} = \frac{1}{9} a^{9}$

查看试题解析
7. 2020年3月，我市某区一周天气质量报告中某项污染指标的数据是：60、60、90、100、90、70、90，则下列关于这组数据表述正确的是（）

A、众数是60 B、中位数是100 C、极差是40 D、平均数是78

查看试题解析
8. 分式方程 $\frac{1}{x}$ ＝ $\frac{2}{x - 2}$ 的解为（）

A、x＝2 B、x＝－2 C、x＝－ $\frac{2}{3}$ D、x＝ $\frac{2}{3}$

查看试题解析
9. 如图，BC是⊙O的直径，点A是⊙O上异于B，C的一点，则∠A的度数为（　　）

A、60° B、70° C、80° D、90°

查看试题解析
10. 直线 $y = 2 x$ 必过的点是（）

A、 $(2, 1)$ B、 $(2, 2)$ C、 $(- 1, - 1)$ D、 $(0, 0)$

查看试题解析
11. 如图，反比例函数y＝ $\frac{2}{x}$ 的图象经过矩形OABC的边AB的中点D，则矩形OABC的面积为（）

A、1 B、2 C、4 D、8

查看试题解析
12. 如图，在正方形 $A B C D$ 中，点 $O$ 是对角线 $A C ， B D$ 的交点，过点 $O$ 作射线分别交 $O M ， O N$ 于点 $E ， F$ ，且 $∠ E O F ＝ 90 °$ ，交 $O C ， E F$ 于点 $G$ ．给出下列结论： $① △ C O E ≌ △ D O F$ ； $② △ O G E ∽ △ F G C$ C； $③$ 四边形 $C E O F$ 的面积为正方形 $A B C D$ 面积的 $\frac{1}{4}$ ； $④ D F^{2} + B E^{2} ＝ O G • O C$ ．其中正确的是（）

A、 $① ② ③ ④$ B、 $① ② ③$ C、 $① ② ④$ D、 $③ ④$

查看试题解析

二、填空题

13. 计算： $- 4 + 3 =$ .

查看试题解析
14. 因式分解： x³y －xy³ .

查看试题解析
15. 一元二次方程 $x^{2} - 1 = 0$ 的解.

查看试题解析
16. 如图，在 $Δ A B C$ 中， $D ， E$ 分别是 $A B 、 A C$ 边上的点， $D E / / B C ， ∠ A D E = 35^{°} ， ∠ C = 120^{°} ，$ 则 $∠ A$ 的度数为.

查看试题解析
17. 在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，把它沿斜边AB所在直线旋转一周，所得几何体的侧面积是.（结果保留π）

查看试题解析
18. 如图，在▱ABCD中，AD=7，AB=2 $\sqrt{3}$ ，∠B=60°.E是边BC上任意一点，沿AE剪开，将△ABE沿BC方向平移到△DCF的位置，得到四边形AEFD，则四边形AEFD周长的最小值为.

查看试题解析

三、解答题

19. 计算： ${(- 1)}^{2} + \sqrt{9} - | - 4 |$

查看试题解析
20. 已知：如图， $A E$ 和 $B D$ 相交于点 $C ， A C = E C ， B C = D C$ ；求证： $A B = E D .$

查看试题解析
21. 求证：四个角都相等的四边形是矩形.

查看试题解析
22. 为推进“传统文化进校园”活动，某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图（每人只能选择一个小组）：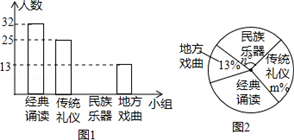

(1)、报名参加课外活动小组的学生共有人，将条形图补充完整；

(2)、扇形图中m= ， n=；

(3)、根据报名情况，学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组，甲、乙恰好都被安排到“地方戏曲”小组的概率是多少？请用列表或画树状图的方法说明.

查看试题解析
23. 深圳天虹某商场从厂家批发电视机进行零售，批发价格与零售价格如下表：

电视机型号

甲

乙

批发价(元/台)

1500

2500

零售价(元/台)

2025

3640

若商场购进甲、乙两种型号的电视机共50台，用去9万元.

(1)、求商场购进甲、乙型号的电视机各多少台？

(2)、迎“元旦”商场决定进行优惠促销：以零售价的七五折销售乙种型号电视机，两种电视机销售完毕，商场共获利8.5%，求甲种型号电视机打几折销售？

查看试题解析
24. 如图是长沙九龙仓国际金融中心，位于长沙市黄兴路与解放路交会处的东北角，投资160亿元人民币，总建筑面积达98万平方米，中心主楼BC高452m，是目前湖南省第一高楼，大楼顶部有一发射塔AB，已知和BC处于同一水平面上有一高楼DE，在楼DE底端D点测得A的仰角为α，tanα＝ $\frac{24}{7}$ ，在顶端E点测得A的仰角为45°，AE＝140 $\sqrt{2}$ m

(1)、求两楼之间的距离CD；

(2)、求发射塔AB的高度．

查看试题解析
25. 如图，在 $Δ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径的 $⊙ O$ 与边 $B C$ ， $A C$ 分别交于D，E两点，过点D作 $D H ⊥ A C$ 于点H.

(1)、判断 $D H$ 与 $⊙ O$ 的位置关系，并说明理由；

(2)、求证： $H$ 为 $C E$ 的中点；

(3)、若 $B C = 10$ ， $\cos C = \frac{\sqrt{5}}{5}$ ，求 $A E$ 的长.

查看试题解析
26. 如图，已知抛物线y= $\frac{1}{3}$ x²+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（-9，10），AC∥x轴，点P是直线AC下方抛物线上的动点.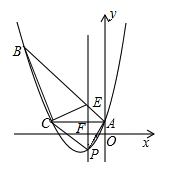

(1)、求抛物线的解析式；

(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；

(3)、当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由.

查看试题解析

电视机型号	甲	乙
批发价(元/台)	1500	2500
零售价(元/台)	2025	3640