广西柳州市2020年数学中考模拟试卷(6月)
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
1. 中国人很早开始使用负数,古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果零上8℃记作+8℃,那么-6℃表示( )A、零下14℃ B、零上6℃ C、零下6℃ D、零上2℃2. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在Rt△ABC中,∠C=90°,BC=4,AC=3,则cosA的值是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 若﹣1<x<0,则 ﹣ =( )A、2x+1 B、1 C、﹣2x﹣1 D、﹣2x+16. 将抛物线y=5(x−1)2+1向上平移2个单位长度,再向右平移3个单位长度,则所得抛物线的解析式为( )A、 B、 C、 D、7. 《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为:今有甲乙二人,不如其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其 的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则可建立方程组为( )A、 B、 C、 D、8. 如图,点A,B,C,D在 上, ∠CAD=30°,∠ACD=50°,则∠ACB=( )
3. 在Rt△ABC中,∠C=90°,BC=4,AC=3,则cosA的值是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 若﹣1<x<0,则 ﹣ =( )A、2x+1 B、1 C、﹣2x﹣1 D、﹣2x+16. 将抛物线y=5(x−1)2+1向上平移2个单位长度,再向右平移3个单位长度,则所得抛物线的解析式为( )A、 B、 C、 D、7. 《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为:今有甲乙二人,不如其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其 的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则可建立方程组为( )A、 B、 C、 D、8. 如图,点A,B,C,D在 上, ∠CAD=30°,∠ACD=50°,则∠ACB=( )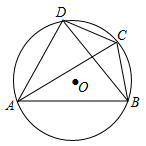 A、 B、 C、 D、9. 某校在“我运动,我快乐”的技能比赛培训活动中,在相同条件下,对甲、乙两名同学的“单手运球”项目进行了5次测试,测试成绩(单位:分)如下:根据右图判断正确的是( )
A、 B、 C、 D、9. 某校在“我运动,我快乐”的技能比赛培训活动中,在相同条件下,对甲、乙两名同学的“单手运球”项目进行了5次测试,测试成绩(单位:分)如下:根据右图判断正确的是( ) A、甲成绩的平均分低于乙成绩的平均分; B、甲成绩的中位数高于乙成绩的中位数; C、甲成绩的众数高于乙成绩的众数; D、甲成绩的方差低于乙成绩的方差.10. 宽与长的比是 (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称美感.我们可以用这样的方法画出黄金矩形:作正方形 ,分别取 的中点 ,连接 ,以点F为圆心,以 为半径画弧,交 的延长线于点G;作 ,交 的延长线于点H,则图中下列矩形是黄金矩形的是( )
A、甲成绩的平均分低于乙成绩的平均分; B、甲成绩的中位数高于乙成绩的中位数; C、甲成绩的众数高于乙成绩的众数; D、甲成绩的方差低于乙成绩的方差.10. 宽与长的比是 (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称美感.我们可以用这样的方法画出黄金矩形:作正方形 ,分别取 的中点 ,连接 ,以点F为圆心,以 为半径画弧,交 的延长线于点G;作 ,交 的延长线于点H,则图中下列矩形是黄金矩形的是( )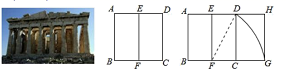 A、矩形ABEF B、矩形EFCD C、矩形EFGH D、矩形ABGH11. 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则DE的长为( )
A、矩形ABEF B、矩形EFCD C、矩形EFGH D、矩形ABGH11. 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则DE的长为( ) A、2.2 B、2.5 C、2 D、1.812. 已知点 ,点 是函数 上的一点,若 (O为坐标原点),则 的面积为( )A、1 B、2 C、3 D、4
A、2.2 B、2.5 C、2 D、1.812. 已知点 ,点 是函数 上的一点,若 (O为坐标原点),则 的面积为( )A、1 B、2 C、3 D、4二、填空题
-
13. 如图,直线 ,直线c与直线a,b都相交.若 ,则 .
 14. 已知x=1是方程x2+bx﹣2=0的一个根,则方程的另一个根是 .15. 因式分解: .16. 已知圆锥的底面积为16 cm2 , 母线长为6cm,则圆锥的侧面积是cm2 .17. 如图1,将边长为a的大正方形剪去一个边长为b的小正方形,并沿图中的虚线剪开,拼接后得到图2,请根据图形的面积写出一个含字母a,b的等式.
14. 已知x=1是方程x2+bx﹣2=0的一个根,则方程的另一个根是 .15. 因式分解: .16. 已知圆锥的底面积为16 cm2 , 母线长为6cm,则圆锥的侧面积是cm2 .17. 如图1,将边长为a的大正方形剪去一个边长为b的小正方形,并沿图中的虚线剪开,拼接后得到图2,请根据图形的面积写出一个含字母a,b的等式.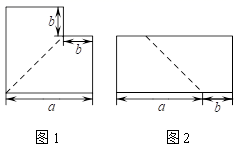 18. 如图,P为长方形 外一点且 .若长方形 的面积为 ,那么 的面积是 .
18. 如图,P为长方形 外一点且 .若长方形 的面积为 ,那么 的面积是 .
三、解答题
-
19. 已知x+y=xy,求代数式 + ﹣(1﹣x)(1﹣y)的值.20. 如图,点 是线段 的中点, , .求证: .
 21. 某市推出电脑上网包月制,每月收取费用y (元)与上网时间x (小时)的函数关系如图所示,其中 是线段,且 轴, 是射线.
21. 某市推出电脑上网包月制,每月收取费用y (元)与上网时间x (小时)的函数关系如图所示,其中 是线段,且 轴, 是射线. (1)、当 时,求y与x之间的函数关系式;(2)、若小李4月份上网35小时,他应付多少元的上网费用?22. 我们用 来表示不超过实数x的最大整数,如 .(1)、若 ,则实数x所有可能取值的范围是.(2)、求方程 的解.23. 中央电视台的“中国诗词大赛”节目文化品位高,内容丰富.某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:
(1)、当 时,求y与x之间的函数关系式;(2)、若小李4月份上网35小时,他应付多少元的上网费用?22. 我们用 来表示不超过实数x的最大整数,如 .(1)、若 ,则实数x所有可能取值的范围是.(2)、求方程 的解.23. 中央电视台的“中国诗词大赛”节目文化品位高,内容丰富.某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题: (1)、扇形统计图中“优秀”所对应扇形的圆心角为度,并将条形统计图补充完整.(2)、此次比赛有四名同学获得满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.24. 已知一次函数 与反比例函数 的图象相交于点A.(1)、求点A的坐标;(2)、若点P是一次函数 图象上的任意一点,求线段 的最小值,并指出此时点P的坐标.
(1)、扇形统计图中“优秀”所对应扇形的圆心角为度,并将条形统计图补充完整.(2)、此次比赛有四名同学获得满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.24. 已知一次函数 与反比例函数 的图象相交于点A.(1)、求点A的坐标;(2)、若点P是一次函数 图象上的任意一点,求线段 的最小值,并指出此时点P的坐标.
