广西北部湾经济区2020年同城中考学科素养测试(四)数学试卷
试卷更新日期:2020-08-10 类型:中考模拟
一、选择题
-
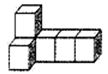
1. ﹣3的相反数为( )A、﹣3 B、﹣ C、 D、32. 如图,用大小一样的正方体搭建一个几何体,该几何体的主视图是( )
 A、
A、 B、
B、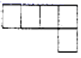 C、
C、 D、
D、 3. 2019年10月1日,为庆祝新中国成立70周年,南京在玄武湖举行了烟花灯光秀.据统计,当晚约有76万人欢聚在玄武湖园内及其周边观看这一表演.数据76万用科学记数法表示为( )A、 7.6×105 B、7.6×106 C、76×105 D、0.76×1064. 下列运算中正确的是( )A、 B、 C、 D、5. 若 ,则下列结论不一定成立的是( )A、 B、 C、 D、6. 如图尺规作业, 为 的平分线,这样的作法依据是( )
3. 2019年10月1日,为庆祝新中国成立70周年,南京在玄武湖举行了烟花灯光秀.据统计,当晚约有76万人欢聚在玄武湖园内及其周边观看这一表演.数据76万用科学记数法表示为( )A、 7.6×105 B、7.6×106 C、76×105 D、0.76×1064. 下列运算中正确的是( )A、 B、 C、 D、5. 若 ,则下列结论不一定成立的是( )A、 B、 C、 D、6. 如图尺规作业, 为 的平分线,这样的作法依据是( )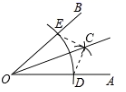 A、 B、 C、 D、7. 已知一个多边形的内角和是外角和的2倍,则此多边形的边数为( )A、6 B、7 C、8 D、98. 如图, 中, , , ,将 绕点A顺时针旋转 得到 ,则 的长为( )
A、 B、 C、 D、7. 已知一个多边形的内角和是外角和的2倍,则此多边形的边数为( )A、6 B、7 C、8 D、98. 如图, 中, , , ,将 绕点A顺时针旋转 得到 ,则 的长为( ) A、2 B、4 C、5 D、69. 如图,等边 的内切圆O切 边于点D,已知等边三角形的边长为12,则图中阴影部分的面积为( )
A、2 B、4 C、5 D、69. 如图,等边 的内切圆O切 边于点D,已知等边三角形的边长为12,则图中阴影部分的面积为( ) A、 B、 C、 D、10. 我图古代《孙子算经》记载“多人共车”问题:“今有三人共车,二车空;二人共车,九人步.问人与车各几何?”意思是说“每三人共乘一辆车,最终剩余2辆车;每2人共乘一辆车,最终有9人无车可乘.问人和车的数量各是多少?”若设有 个人,则可列方程是( )A、 B、 C、 D、11. 如图,抛物线 的对称轴为直线 ,与x轴的一个交点坐标为 ,其部分图象如图所示,下列结论:① ;② ;③当 时,x的取值范围是 ;④当 时,y随x增大而增大;⑤若t为任意实数,则有 ,其中结论正确的个数是( )
A、 B、 C、 D、10. 我图古代《孙子算经》记载“多人共车”问题:“今有三人共车,二车空;二人共车,九人步.问人与车各几何?”意思是说“每三人共乘一辆车,最终剩余2辆车;每2人共乘一辆车,最终有9人无车可乘.问人和车的数量各是多少?”若设有 个人,则可列方程是( )A、 B、 C、 D、11. 如图,抛物线 的对称轴为直线 ,与x轴的一个交点坐标为 ,其部分图象如图所示,下列结论:① ;② ;③当 时,x的取值范围是 ;④当 时,y随x增大而增大;⑤若t为任意实数,则有 ,其中结论正确的个数是( )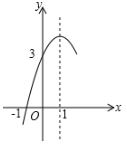 A、4个 B、3个 C、2个 D、1个12. 如图,等边 的边长为 ,以O为圆心, 为直径的半圆经过点A,连接 , 相交于点P,将等边 从 与 重合的位置开始,绕着点O顺时针旋转 ,交点P运动的路径长是( )
A、4个 B、3个 C、2个 D、1个12. 如图,等边 的边长为 ,以O为圆心, 为直径的半圆经过点A,连接 , 相交于点P,将等边 从 与 重合的位置开始,绕着点O顺时针旋转 ,交点P运动的路径长是( )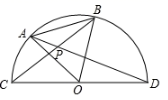 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
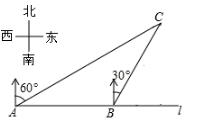
13. 若二次根式 有意义,则x的取值范围为 .14. 把 因式分解的结果是.15. 一个不透明的袋子中装有黑、白小球各两个,这些小球除颜色外无其他差别,从袋子中随机摸出两个小球,则摸出的小球都是黑球的概率为.16. 如图,在一笔直的海岸线 上有相距 的 两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东 的方向上,从B站测得船C在北偏东 的方向上,则船C到海岸线 的距离是 .
 17. 如图,在菱形 中, , 在 上,将 沿 翻折至 ,且 刚好过 的中点P,则 .
17. 如图,在菱形 中, , 在 上,将 沿 翻折至 ,且 刚好过 的中点P,则 . 18. 如图,点A、B在函数 ( , 且 是常数)的图象上,且点A在点B的左侧过点A作 轴,垂足为M,过点B作 轴,垂足为N, 与 的交点为C,连结 、 .若 和 的面积分别为1和4,则k的值为.
18. 如图,点A、B在函数 ( , 且 是常数)的图象上,且点A在点B的左侧过点A作 轴,垂足为M,过点B作 轴,垂足为N, 与 的交点为C,连结 、 .若 和 的面积分别为1和4,则k的值为.
三、解答题
-
19. 计算:20. 解不等式组: ,并将其解集表示在数轴上.21. 如图, 三个顶点的坐标分别为 、 、 .
 (1)、画出 关于 轴的对称图形 ;(2)、画出将 绕原点O按顺时针旋转 所得的 ;(3)、在 轴上求作一点P,使 的周长最小,并直接写出点P的坐标.(不写解答过程,直接写出结果)22. 如图,平行四边形 的对角线 、 交于点O,分别过点C、D作CF∥BD,DF∥AC,连接 交 于点E.
(1)、画出 关于 轴的对称图形 ;(2)、画出将 绕原点O按顺时针旋转 所得的 ;(3)、在 轴上求作一点P,使 的周长最小,并直接写出点P的坐标.(不写解答过程,直接写出结果)22. 如图,平行四边形 的对角线 、 交于点O,分别过点C、D作CF∥BD,DF∥AC,连接 交 于点E.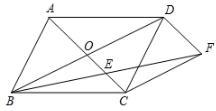 (1)、求证: ;(2)、当 满足什么条件时,四边形 为菱形?请说明理由.23. 良好的饮食对学生的身体、智力发育和健康起到了极其重要的作用,荤菜中蛋白质、钙、磷及脂溶性维生素优于素食,而素食中不饱和脂肪酸、维生素和纤维素又优于荤食,只有荤食与素食适当搭配,才能强化初中生的身体素质.某校为了了解学生的体质健康状况,以便食堂为学生提供合理膳食,对本校七年级、八年级学生的体质健康状况进行了调查,过程如下:
(1)、求证: ;(2)、当 满足什么条件时,四边形 为菱形?请说明理由.23. 良好的饮食对学生的身体、智力发育和健康起到了极其重要的作用,荤菜中蛋白质、钙、磷及脂溶性维生素优于素食,而素食中不饱和脂肪酸、维生素和纤维素又优于荤食,只有荤食与素食适当搭配,才能强化初中生的身体素质.某校为了了解学生的体质健康状况,以便食堂为学生提供合理膳食,对本校七年级、八年级学生的体质健康状况进行了调查,过程如下:收集数据:
从七、八年级两个年级中各抽取15名学生,进行了体质健康测试,测试成绩(百分制)如下:
七年级:74 81 75 76 70 75 75 79 81 70 74 80 91 69 82
八年级:81 94 83 77 83 80 81 70 81 73 78 82 80 70 50
整理数据:
年级
七年级
0
10
4
1
八年级
1
8
1
(说明:90分及以上为优秀,80~90分(不含90分)为良好,60~80分(不含80分)为及格,60分以下为不及格)
分析数据:
年级
平均数
中位数
众数
七年级
b
c
75
八年级
77.5
80
d
得出结论:
(1)、根据上述数据,写出 的值;(2)、可以推断出哪个年级学生的体质状况更好一些,并说明理由;(3)、若七年级共有300名,请估计七年级体质成绩优秀的人数.24. 某汽车制造厂开发一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.(1)、每名熟练工和新工人每月分别可以安装多少辆电动汽车?(2)、如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?(3)、在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?25. 如图1,在 中, , 是 的外接圆,过点 作 交 于点 ,连接 交 于点 ,延长 至点 ,使 ,连接 .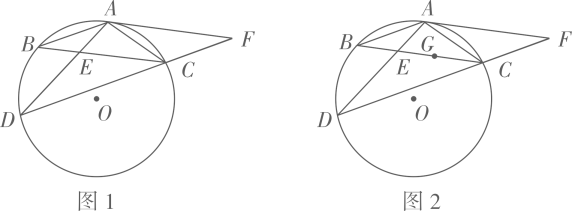 (1)、求证: ;(2)、求证: 是 的切线;(3)、如图2,若点 是 的内心, ,求 的长.26. 已知,如图,抛物线 的顶点为 ,经过抛物线上的两点 和 的直线交抛物线的对称轴于点 .
(1)、求证: ;(2)、求证: 是 的切线;(3)、如图2,若点 是 的内心, ,求 的长.26. 已知,如图,抛物线 的顶点为 ,经过抛物线上的两点 和 的直线交抛物线的对称轴于点 .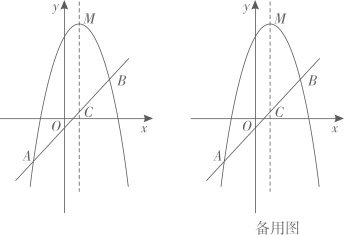 (1)、求抛物线的解析式和直线 的解析式.(2)、在抛物线上 两点之间的部分(不包含 两点),是否存在点 ,使得 ?若存在,求出点 的坐标;若不存在,请说明理由.(3)、若点 在抛物线上,点 在 轴上,当以点 为顶点的四边形是平行四边形时,直接写出满足条件的点 的坐标.
(1)、求抛物线的解析式和直线 的解析式.(2)、在抛物线上 两点之间的部分(不包含 两点),是否存在点 ,使得 ?若存在,求出点 的坐标;若不存在,请说明理由.(3)、若点 在抛物线上,点 在 轴上,当以点 为顶点的四边形是平行四边形时,直接写出满足条件的点 的坐标.