广西北部湾经济区2020年同城中考学科素养测试（三）数学试卷

试卷更新日期：2020-08-10 类型：中考模拟

进入出卷网下载

一、选择题

1. 计算 ${(- 4)}^{3}$ 的结果等于（）

A、-12 B、12 C、-64 D、64

查看试题解析
2. $t a n 30^{\circ}$ 的值等于（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\sqrt{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
3. 下列美丽的图案中，既是轴对称图形又是中心对称图形的个数是（）

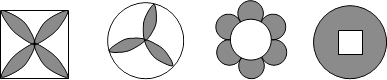A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 某城区青年在“携手添绿，美丽共创”植树活动中，共栽植、养护树木15000株将15000用科学记数法表示为（）

A、 $1.5 \times 10^{4}$ B、 $15 \times 10^{3}$ C、 $1.5 \times 10^{5}$ D、 $0.15 \times 10^{6}$

查看试题解析
5. 如图是一个大正方体切去一个小正方体形成的几何体，它的左视图是（）

A、 B、 C、 D、

查看试题解析
6. 若 $a = \sqrt{30}$ ， $b = | - 6 |$ ， $c = \sqrt[3]{65}$ 则下列关系正确的为（）

A、 $a > b > c$ B、 $c > b > a$ C、 $b > a > c$ D、 $b > c > a$

查看试题解析
7. 计算 $\frac{x^{2} + 1}{x - 6} \cdot \frac{x^{2} - 36}{x^{3} + x}$ 的结果为（）

A、 $\frac{x + 6}{x}$ B、 $\frac{x}{x - 6}$ C、 $\frac{x}{x + 6}$ D、 $x + 6$

查看试题解析
8. 下列方程中，有两个不相等的实数根的方程是（）

A、 $x^{2} -8x+17=0$ B、 $x^{2} -6x-10=0$ C、 $x^{2} -4 \sqrt{2} x+9=0$ D、 $x^{2} -4x+4=0$

查看试题解析
9. 若点 $A (-3 ， y_{1})$ ， $B (-1 ， y_{2})$ ， $C (2 ， y_{3})$ 在反比例函数 $y= \frac{k^{2} +1}{x}$ ( $k$ 为常数)的图象上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{2} < y_{1} < y_{3}$ B、 $y_{1} < y_{2} < y_{3}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
10. 如图，点O是等边三角形 $ABC$ 内的一点， $∠ BOC=150 °$ ，将 $Δ BCO$ 绕点C按顺时针旋转 $60 °$ 得到 $Δ ACD$ ，则下列结论不正确的是（）

A、 $BO=AD$ B、 $∠ DOC=60 °$ C、 $OD ⊥ AD$ D、 $OD//AB$

查看试题解析
11. 如图，已知菱形 $ABCD$ ， $AB=4$ ， $∠ BAD=120 °$ ，E为 $BC$ 中点，P为对角线 $BD$ 上一点，则 $PE+PC$ 的最小值等于（）

A、 $2 \sqrt{2}$ B、 $2 \sqrt{3}$ C、 $2 \sqrt{5}$ D、8

查看试题解析
12. 如图所示，抛物线L：y＝ax²+bx+c（a＜0）的对称轴为x＝5，且与x轴的左交点为(1，0)，则下列说法正确的有（）
①C(9，0)；②b+c＞﹣10；③y的最大值为﹣16a；④若该抛物线与直线y＝8有公共交点，则a的取值范围是a≤ $\frac{1}{2}$ ．

A、①②③④ B、①②③ C、①③④ D、①④

查看试题解析

二、填空题

13. 因式分解 $- 16 x^{4} + y^{4}$ 的结果是.

查看试题解析
14. 计算 $(a - 2 b) (a^{2} + 2 a b + 4 b^{2})$ 的结果是.

查看试题解析
15. 一个不透明的口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4随机摸出1个小球，不放回，再随机摸出1个小球，两次摸出的小球标号的积小于4的概率是

查看试题解析
16. 将函数 $y=-2x$ 的图象向下平移 $n$ 个单位得到的图象经过点(2，-8)，那么 $n$ 的值等于.

查看试题解析
17. 如图， $Rt Δ ABC$ 中， $∠ ACB=90 °$ ， $AC=CB=4 \sqrt{2}$ ， $∠ BAD= ∠ ADE=60 °$ ， $AD=5$ ， $CE$ 平分 $∠ ACB$ ， $DE$ 与 $CE$ 相交于点 $E$ ，则 $DE$ 的长等于.

查看试题解析
18. 如图，在正方形 $A B C D$ 中，点 $E 、 F$ 分别是边 $A D 、 B C$ 的中点，连接 $D F ，$ 过点E作 $E H ⊥ D F ，$ 垂足为 $H ， E H$ 的延长线交 $D C$ 于点G.过点 $H$ 作 $M N / / C D ，$ 分别交 $A D 、 B C$ 于 $M 、 N ，$ 正方形 $A B C D$ 的边长为 $10$ ，下列四个结论：① $C F = \frac{3}{2} D G ，$ ② $t a n ∠ D H M = \frac{1}{3}$ ；③ $S_{四边形 C F H G} = \frac{95}{4}$ ；④若点 $P$ 是 $M N$ 上一点，则 $△ P C D$ 周长的最小值为 $10 + 2 \sqrt{26}$ ，其中正确的结论有.

查看试题解析

三、解答题

19. 计算: ${(- \frac{1}{2})}^{- 1} + 2 c o s 60 ° + {(π - 2019)}^{0}$ .

查看试题解析
20. 解不等式组 ${\begin{cases} 2 x - 1 > x + 1 ① \\ 4 x \leq 3 x + 5 ② \end{cases}$ 并把它的解集在数轴上表示出来.

查看试题解析
21. 如图，已知 $△ A B C$ 的三个顶点的坐标分别为 $A (- 6 ， 4) ， B (- 4 ， 0) ， C (- 2 ， 2)$ .

（1）将 $△ A B C$ 向右平移5个单位得 $△ A_{1} B_{1} C_{1} ，$ 画出图形，并直接写出点 $A_{1}$ 的坐标；
（2）将 $△ A B C$ 绕坐标原点O逆时针旋转 $90 °$ ，得 $△ A_{2} B_{2} C_{2} ，$ 画出图形，并直接写出点 $B_{2}$ 的坐标.

查看试题解析
22. 为了促进学生全面发展，河南省某地区教育局在全区中小学开展“书法、手球、豫剧进校园”活动今年8月份，该区某校举行了“朝阳沟”演唱比赛、比赛分 $A 、 B 、 C 、 D 、 E$ 五个等级，该校部分学生参加了学校的比赛，并将比赛结果绘制成如下两幅不完整的统计图，请根据图中信息，解答下列问题：

(1)、求该校参加本次“朝阳沟”演唱比赛的学生人数；

(2)、求扇形统计图B等级所对应扇形的圆心角度数；

(3)、已知A等级的4名学生中有2名男生，2名女生，现从中任意选取2名学生作为全校学生的楷模请你用列表法或画树状图的方法求出恰好选1男1女的概率.

查看试题解析
23. 如图，分别以 $R t △ A B C$ 的直角边 $A C$ 及斜边 $A B$ 向外作等边 $△ A C D$ 、等边 $△ A B E ，$ 已知 $∠ B A C = 30 ° ， E F ⊥ A B$ ，垂足为F，连接 $D F$ .

(1)、求证： $B C = A F$ ；

(2)、求证：四边形 $A D F E$ 是平行四边形；

查看试题解析

24. 甲、乙两家商场平时以同样价格出售相同的商品，春节期间两家商场都让利酬宾，其中甲商场所有商品按8折出售，乙商场对一次购物中不超过200元的不打折，超过200元后的价格部分打

7

折.设商品原价为x元，顾客购物金额为y元.

(1)、根据题意，填写如表：

商品原价	100	150	250	······
甲商场购物金额(元)	80			······
乙商场购物金额(元)	100			······

(2)、分别就两家商场的让利方式写出

y

关于

x

的函数关系式；

(3)、若

x > 2500

时，选择哪家商场去购物更省钱?并说明理由.

查看试题解析

25. 如图， $Rt Δ ACB$ 中， $∠ ACB=90 °$ ， $O$ 为 $AB$ 上一点， $⊙ O$ 经过点A，与 $AC$ 相交于点E，与 $AB$ 交于点F，连接 $EF$ .

(1)、.如图，若 $∠ B=30 °$ ， $AE=2$ ，求 $AF$ 的长.

(2)、如图， $DA$ 平分 $∠ CAB$ ，交 $CB$ 于点 $D$ ， $⊙ O$ 经过点 $D$ .
①求证： $BC$ 为 $⊙ O$ 的切线；

②若 $AE=3$ ， $CD=2$ ，求 $AF$ 的长.

查看试题解析
26. 如图，在平面直角坐标系中，抛物线 $y = \frac{1}{6} x^{2} + b x + c$ 经过原点O，与x轴交于点A(5，0)，第一象限的点C(m，4)在抛物线上，y轴上有一点B(0，10).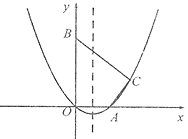

(I)求抛物线的解析式及它的对称轴；

(Ⅱ)点 $P (0 ， n)$ 在线段OB上，点Q在线段BC上，若 $O P = 2 B Q$ ，且 $P A = Q A$ ，求n的值；

(Ⅲ)在抛物线的对称轴上，是否存在点M，使以A，B，M为顶点的三角形是等腰三形？若存在，求出点M的坐标；若不存在，请说明理由.

查看试题解析