黑龙江省哈尔滨市五常市2019-2020学年九年级上学期数学12月月考试卷
试卷更新日期:2020-08-10 类型:月考试卷
一、单选题
-
1. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、2. 下列等式正确的是( )A、( )2=3 B、 =﹣3 C、 =3 D、(﹣ )2=﹣33. 下列图案中,是轴对称图形而不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 抛物线 与y轴的交点坐标为( )A、 B、 C、 D、5. 如图是由五个大小相同的立方体搭成的几何体,其左视图是( )
4. 抛物线 与y轴的交点坐标为( )A、 B、 C、 D、5. 如图是由五个大小相同的立方体搭成的几何体,其左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 在 中, ,则 边的长为( )
6. 在 中, ,则 边的长为( ) A、 B、 C、 D、7. 如图,在 中, 是弦, 切 于点 ,交射线 于点 ,若 ,则 的度数为( )
A、 B、 C、 D、7. 如图,在 中, 是弦, 切 于点 ,交射线 于点 ,若 ,则 的度数为( ) A、 B、 C、 D、8. 如图,在 纸片中, ,将 绕着点A按逆时针方向旋转到 的位置(点B’、C’分别为点B、C的对应点),连接 ,若' ,则 的度数为( )
A、 B、 C、 D、8. 如图,在 纸片中, ,将 绕着点A按逆时针方向旋转到 的位置(点B’、C’分别为点B、C的对应点),连接 ,若' ,则 的度数为( ) A、 B、 C、 D、9. 将一件商品八折销售后,所获利润比按原价销售少30元,该商品的原价为( )A、 元 B、 元 C、 元 D、 元10. 如图,在 中,点D在BC边上,连接AD,点G在线段AD上,过点G作 ,交 边于点E,作 ,交BC边于点F,则下列结论中一定正确的是( )
A、 B、 C、 D、9. 将一件商品八折销售后,所获利润比按原价销售少30元,该商品的原价为( )A、 元 B、 元 C、 元 D、 元10. 如图,在 中,点D在BC边上,连接AD,点G在线段AD上,过点G作 ,交 边于点E,作 ,交BC边于点F,则下列结论中一定正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
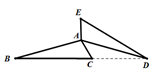
11. 抛物线 的顶点坐标是12. 在二次根式 中,x的取值范围是 .13. 计算 的结果是 .14. 如图,将 绕点A逆时针旋转 ,得到 ,这时点 恰好在同一直线上,则 的度数为 .
 15. 若 是一元二次方程 的一个根,则a的值为 .16. 一个扇形的面积为10π,弧长为4π,则此扇形的圆心角度数为 .17. 不透明的袋子中装有 个白球和 个黑球,它们除颜色外其余均相同,随机从中摸取一个球后放回,再随机摸取一个球,则两次摸取的球颜色不同的概率为 .18. 如图, 内接于 ,若 ,则 的半径长为 .
15. 若 是一元二次方程 的一个根,则a的值为 .16. 一个扇形的面积为10π,弧长为4π,则此扇形的圆心角度数为 .17. 不透明的袋子中装有 个白球和 个黑球,它们除颜色外其余均相同,随机从中摸取一个球后放回,再随机摸取一个球,则两次摸取的球颜色不同的概率为 .18. 如图, 内接于 ,若 ,则 的半径长为 . 19. 在 中, ,将线段 绕点 顺时针旋转 ,点 落在直线 上的点 处,若 ,则 边的长为 .20. 如图,在 中, 于点D,点E在线段BD上,F为AC边的中点,将线段EF绕点E逆时针旋转得到EG,点G落在AB边上,若 , , ,则线段EF的长为 .
19. 在 中, ,将线段 绕点 顺时针旋转 ,点 落在直线 上的点 处,若 ,则 边的长为 .20. 如图,在 中, 于点D,点E在线段BD上,F为AC边的中点,将线段EF绕点E逆时针旋转得到EG,点G落在AB边上,若 , , ,则线段EF的长为 . 21. 先化简,再求代数式 的值,其中 .
21. 先化简,再求代数式 的值,其中 .三、解答题
-
22. 如图,在5X5的正方形网格中,每个小正方形的边长均为 ,线段 的端点 均在小正方形的顶点上,请按要求画出图形并计算:

①以 为一边画出 ,使其是等腰直角三角形,点 在小正方形的顶点上,且 的面积为 ;
②以 为一边画出 ,使得 ,点 在小正方形的顶点上,且 的面积最大;
③连接 ,并直接写出四边形 的面积.
23. 胜利中学从全校学生中随机选取一部分学生,对他们每周上网的时间t进行调查,调查情况分为: 小时; 小时 小时; 小时 小时; 小时四种,并将统计结果制成了如下两幅不完整的统计图,请根据图中信息解答下列问题: (1)、求参加调查的学生的人数;(2)、求扇形图中 组扇形的圆心角度数,并通过计算补全条形统计图;(3)、在所调查的学生中,随机选取一名学生,求他每周上网时间大于 小时的概率.24. 如图,在平面直角坐标系中, 为坐标原点,某反比例函数的图象经过点 .
(1)、求参加调查的学生的人数;(2)、求扇形图中 组扇形的圆心角度数,并通过计算补全条形统计图;(3)、在所调查的学生中,随机选取一名学生,求他每周上网时间大于 小时的概率.24. 如图,在平面直角坐标系中, 为坐标原点,某反比例函数的图象经过点 . (1)、求该反比例函数的解析式;(2)、点 和 均在该反比例函数的图象上,点p在x轴上,请画出使 的值最小的p点位置,并求出此时点p的坐标.25. 某商店经销一种产品,其标价比进价每件多7元,且商店用80元购进这种商品的数量和这种商品150元的销售额所售出的件数相同.(1)、求这种商品的进价及标价;(2)、经过一段时间的销售,商店发现,以标价出售这种商品,每天可售出 件,每涨价 元,则少卖出 件,要使这种商品每天的销售额最大,求该商品每件应涨价多少元.26. 内接于 边于点 ,连接 .(1)、如图1,求证: ;
(1)、求该反比例函数的解析式;(2)、点 和 均在该反比例函数的图象上,点p在x轴上,请画出使 的值最小的p点位置,并求出此时点p的坐标.25. 某商店经销一种产品,其标价比进价每件多7元,且商店用80元购进这种商品的数量和这种商品150元的销售额所售出的件数相同.(1)、求这种商品的进价及标价;(2)、经过一段时间的销售,商店发现,以标价出售这种商品,每天可售出 件,每涨价 元,则少卖出 件,要使这种商品每天的销售额最大,求该商品每件应涨价多少元.26. 内接于 边于点 ,连接 .(1)、如图1,求证: ; (2)、如图2,延长 交 于点 ,点 在线段 上,射线 交 边于点 ,连接 ,若 ,求证: ;
(2)、如图2,延长 交 于点 ,点 在线段 上,射线 交 边于点 ,连接 ,若 ,求证: ; (3)、如图3,在 的条件下,连接 ,若 , ,求线段 的长.
(3)、如图3,在 的条件下,连接 ,若 , ,求线段 的长. 27. 在平面直角坐标系中,点 为坐标原点,抛物线 交 轴的负半轴于点 ,交 轴的正半轴于点 ,交 轴于点 ,且 .(1)、求 的值;(2)、如图1,点 在第四象限的抛物线上,横坐标为 连接 ,交 轴于点 ,设 ,求 与 之间的函数关系式,并直接写出自变量 的取值范围;
27. 在平面直角坐标系中,点 为坐标原点,抛物线 交 轴的负半轴于点 ,交 轴的正半轴于点 ,交 轴于点 ,且 .(1)、求 的值;(2)、如图1,点 在第四象限的抛物线上,横坐标为 连接 ,交 轴于点 ,设 ,求 与 之间的函数关系式,并直接写出自变量 的取值范围; (3)、如图2,在 的条件下,连接 ,交 轴于点 ,点 在线段 上,射线 交 于点 ,点 在第二象限的抛物线上,连接 ,将线段 绕点 顺时针旋转 得到线段 ,连接 ,若 , ,求点 和 的坐标.
(3)、如图2,在 的条件下,连接 ,交 轴于点 ,点 在线段 上,射线 交 于点 ,点 在第二象限的抛物线上,连接 ,将线段 绕点 顺时针旋转 得到线段 ,连接 ,若 , ,求点 和 的坐标.