河南省非凡吉创联盟2019-2020学年高一名校上学期数学12月调研试卷
试卷更新日期:2020-08-10 类型:月考试卷
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 函数 的定义域为( )A、 B、 C、 D、3. 下列命题中,正确的是( )
①在圆柱上、下底面圆周上各取一点,则这两点的连线是圆柱的母线;②圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;③在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.
A、①② B、②③ C、②④ D、③④4. 函数 的零点所在区间是( )A、 B、(0,1) C、(1,2) D、(2,3)5. 设 , , ,则 的大小关系是( )A、 B、 C、 D、6. 已知四棱锥 的三视图如图所示,其侧面积等于 ,则其体积是( )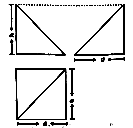 A、 B、 C、 D、87. 的图像为( )A、
A、 B、 C、 D、87. 的图像为( )A、 B、
B、 C、
C、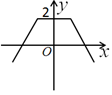 D、
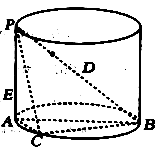
D、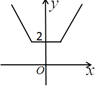 8. 函数 的单调递增区间是( )A、 B、 C、 D、9. 已知平面四边形 ,按照斜二测画法( )画出它的直观图 是边长为1的正方形(如图所示),则原平面四边形 的面积是( )
8. 函数 的单调递增区间是( )A、 B、 C、 D、9. 已知平面四边形 ,按照斜二测画法( )画出它的直观图 是边长为1的正方形(如图所示),则原平面四边形 的面积是( )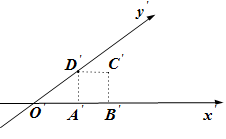 A、 B、 C、 D、10. 已知直三棱柱 的底面为直角三角形,且两直角边长分别为1和 ,此三棱柱的高为 ,则该三棱柱的外接球的表面积为( )A、 B、 C、 D、11. 已知函数 若 有三个不等实数根 ,则 的取值范围是( )A、 B、 C、 D、12. 为了提高资源利用率,2019年全国掀起了垃圾分类的热潮,垃圾分类已经成为新时尚.假设某市2019年全年用于垃圾分类的资金为5000万元,在此基础上,每年投入的资金比上一年增长20%,则该市全年用于垃圾分类的资金开始超过12800万元的年份是( )(参考数据: )A、2022年 B、2023年 C、2024年 D、2025年
A、 B、 C、 D、10. 已知直三棱柱 的底面为直角三角形,且两直角边长分别为1和 ,此三棱柱的高为 ,则该三棱柱的外接球的表面积为( )A、 B、 C、 D、11. 已知函数 若 有三个不等实数根 ,则 的取值范围是( )A、 B、 C、 D、12. 为了提高资源利用率,2019年全国掀起了垃圾分类的热潮,垃圾分类已经成为新时尚.假设某市2019年全年用于垃圾分类的资金为5000万元,在此基础上,每年投入的资金比上一年增长20%,则该市全年用于垃圾分类的资金开始超过12800万元的年份是( )(参考数据: )A、2022年 B、2023年 C、2024年 D、2025年二、填空题
-
13. 函数 恒过定点14. ,则 .15. 圆柱的侧面展开图是一个面积为 的正方形,该圆柱内有一个体积为 的球,则 的最大值为 .16. 已知定义在R上的奇函数 ,对任意的 都满足 ,且当 时, ,则 .
三、解答题
-
17. 已知全集 ,集合 , .(1)、当 时,求 与 .(2)、若 ,求实数m的取值范围.18. 已知函数 .
(Ⅰ)求满足 的实数 的值;
(Ⅱ)求 时函数 的值域.
19. 如图,正方体 的棱长为a,连接 , , , , , ,得到一个三棱锥,求: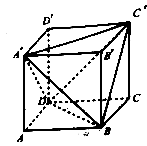 (1)、三棱锥 的表面积与正方体表面积的比值;(2)、三棱锥 的体积.20. 暑假期间,某旅行社为吸引游客去某风景区旅游,推出如下收费标准:若旅行团人数不超过30,则每位游客需交费用600元;若旅行团人数超过30,则游客每多1人,每人交费额减少10元,直到达到70人为止.(1)、写出旅行团每人需交费用 (单位:元)与旅行团人数 之间的函数关系式;(2)、旅行团人数为多少时,旅行社可以从该旅行团获得最大收入?最大收入是多少?
(1)、三棱锥 的表面积与正方体表面积的比值;(2)、三棱锥 的体积.20. 暑假期间,某旅行社为吸引游客去某风景区旅游,推出如下收费标准:若旅行团人数不超过30,则每位游客需交费用600元;若旅行团人数超过30,则游客每多1人,每人交费额减少10元,直到达到70人为止.(1)、写出旅行团每人需交费用 (单位:元)与旅行团人数 之间的函数关系式;(2)、旅行团人数为多少时,旅行社可以从该旅行团获得最大收入?最大收入是多少?