初中数学青岛版九年级上学期 第1章 1.2怎样判定三角形相似
试卷更新日期:2020-08-08 类型:同步测试
一、单选题
-
1. 下列两个三角形不一定相似的是( )A、两条直角边的比都是 的两个直角三角形 B、腰与底的比都是 的两个等腰三角形 C、有一个内角为 的两个直角三角形 D、有一个内角为 的两个等腰三角形2. 下列命题中正确的有( )
①有一个角等于80°的两个等腰三角形相似;②两边对应成比例的两个等腰三角形相似;③有一个角对应相等的两个等腰三角形相似;④底边对应相等的两个等腰三角形相似.
A、0个 B、1个 C、2个 D、3个3. 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( ) A、 = B、 = C、 = D、 =4. 如图,点D、E分别在△ABC的AB、AC边上,下列条件中:①∠ADE=∠C;② ;③ .使△ADE与△ACB一定相似的是( )
A、 = B、 = C、 = D、 =4. 如图,点D、E分别在△ABC的AB、AC边上,下列条件中:①∠ADE=∠C;② ;③ .使△ADE与△ACB一定相似的是( )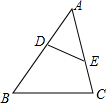 A、①② B、②③ C、①③ D、①②③5. 如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
A、①② B、②③ C、①③ D、①②③5. 如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )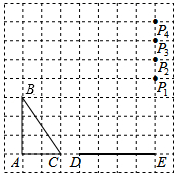 A、P1 B、P2 C、P3 D、P46. 已知:如图,Rt△ABC中,∠BAC=90°,D是AC上一点,∠ABD=∠C,直线EF过点D,与BA的延长线相交于F,且EF⊥BC,垂足为E.则图中所有与△ABD相似的三角形有多少个( )
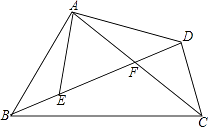
A、P1 B、P2 C、P3 D、P46. 已知:如图,Rt△ABC中,∠BAC=90°,D是AC上一点,∠ABD=∠C,直线EF过点D,与BA的延长线相交于F,且EF⊥BC,垂足为E.则图中所有与△ABD相似的三角形有多少个( )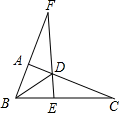 A、3 B、4 C、5 D、67. 如图,下列条件不能判定△ADB∽△ABC的是( )
A、3 B、4 C、5 D、67. 如图,下列条件不能判定△ADB∽△ABC的是( )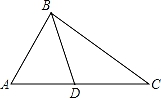 A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、 =8. 已知△ABC的三边长为8,12,18,又知△A1B1C1也有一边长为12,且与△ABC相似而不全等,则这样的△A1B1C1的个数为( )A、0 B、1 C、2 D、39. 如图,在正三角形ABC中,点D、E分别在AC、AB上,且 ,AE=BE,则有( )
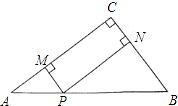
A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、 =8. 已知△ABC的三边长为8,12,18,又知△A1B1C1也有一边长为12,且与△ABC相似而不全等,则这样的△A1B1C1的个数为( )A、0 B、1 C、2 D、39. 如图,在正三角形ABC中,点D、E分别在AC、AB上,且 ,AE=BE,则有( )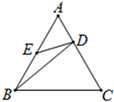 A、△AED∽△BED B、△AED∽△CBD C、△AED∽△ABD D、△BAD∽△BCD10. 如图,P是Rt△ABC的斜边BC上异于端点B,C的点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )
A、△AED∽△BED B、△AED∽△CBD C、△AED∽△ABD D、△BAD∽△BCD10. 如图,P是Rt△ABC的斜边BC上异于端点B,C的点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )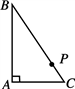 A、1条 B、2条 C、3条 D、4条11. 如图,BD是四边形ABCD的对角线,若∠ABD=∠C=90°,则添加下列条件仍不能判断△ABD∽△DCB的是( )
A、1条 B、2条 C、3条 D、4条11. 如图,BD是四边形ABCD的对角线,若∠ABD=∠C=90°,则添加下列条件仍不能判断△ABD∽△DCB的是( )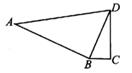 A、AD∥BC B、AD⊥CD C、BD2=AD·BC D、BD平分∠ADC12. 如图,△ABC和阴影三角形的顶点都在小正方形的顶点上,则与△ABC相似的阴影三角形为( )
A、AD∥BC B、AD⊥CD C、BD2=AD·BC D、BD平分∠ADC12. 如图,△ABC和阴影三角形的顶点都在小正方形的顶点上,则与△ABC相似的阴影三角形为( )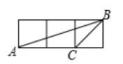 A、
A、 B、
B、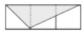 C、
C、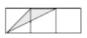 D、
D、
二、填空题
-
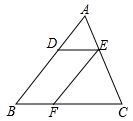
13. 如图,在△ABC中,D、E、F分别为边AB、AC、BC上的点,连接DE、EF。若DE∥BC,EF∥AB,则图中共有对相似三角形.
 14. 如图,AD∥BC,∠D=90°,AD=2,BC=6,DC=8,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有个.
14. 如图,AD∥BC,∠D=90°,AD=2,BC=6,DC=8,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有个.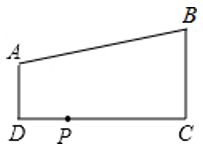 15. 如图,在正方形网格上有6个斜三角形:
15. 如图,在正方形网格上有6个斜三角形: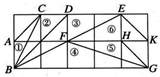
①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.
在②~⑥中,与①相似的三角形的序号是.(把你认为正确的都填上)
16.如图,在△ABC中,AB=AC,点D在边BC上,连接AD,将线段AD绕点A逆时针旋转到AE,使得∠DAE=∠BAC,连接DE交AC于F,请写出图中一对相似的三角形:(只要写出一对即可).
 17. 如图,在 中, , ,点P是AB边的中点,点Q是BC边上一个动点,当 时, 与 相似.
17. 如图,在 中, , ,点P是AB边的中点,点Q是BC边上一个动点,当 时, 与 相似.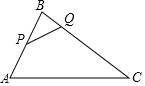 18. 如图所示,在△ABC中,AB=8cm,BC=16cm.点P从点A出发沿AB向点B以2cm/s的速度运动,点Q从点B出发沿BC向点C以4cm/s的速度运动.如果点P,Q分别从点A,B同时出发,则秒钟后△PBQ与△ABC相似?
18. 如图所示,在△ABC中,AB=8cm,BC=16cm.点P从点A出发沿AB向点B以2cm/s的速度运动,点Q从点B出发沿BC向点C以4cm/s的速度运动.如果点P,Q分别从点A,B同时出发,则秒钟后△PBQ与△ABC相似?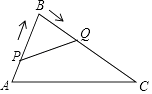 19. 如图,在直角形坐标系中有两点A(6,0)、B(0,8),点C为AB的中点,点D在x轴上,当点D的坐标为时,由点A、C、D组成的三角形与△AOB相似.
19. 如图,在直角形坐标系中有两点A(6,0)、B(0,8),点C为AB的中点,点D在x轴上,当点D的坐标为时,由点A、C、D组成的三角形与△AOB相似.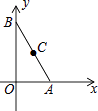 20.
20.如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是 .
①BE=CD;②∠BOD=60°;③△BOD∽△COE.

三、作图题
-
21. 如图
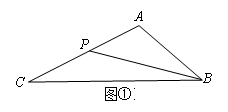
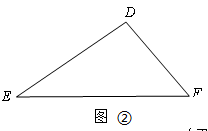 (1)、如图①,在△ABC中,AB=m,AC=n(n>m),点P在边AC上.当AP=时,△APB∽△ABC;(2)、如图②,已知△DEF(DE>DF),请用直尺和圆规在直线DF上求作一点Q,使DE是线段DF和DQ的比例项.(保留作图痕迹,不写作法)
(1)、如图①,在△ABC中,AB=m,AC=n(n>m),点P在边AC上.当AP=时,△APB∽△ABC;(2)、如图②,已知△DEF(DE>DF),请用直尺和圆规在直线DF上求作一点Q,使DE是线段DF和DQ的比例项.(保留作图痕迹,不写作法)四、解答题
-
22. 如图, ,求证: 与 相似.
 23. 已知,如图, = = ,那么△ABD与△BCE相似吗?为什么?
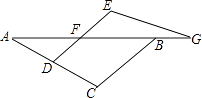
23. 已知,如图, = = ,那么△ABD与△BCE相似吗?为什么?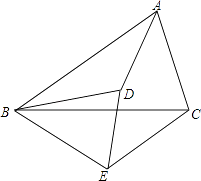 24. 甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”.
24. 甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”.甲同学的解答得到了老师的好评.
乙同学的解答是这样的:“与△ABC相似的三角形只有△AFD,证明如下:
∵DF∥CB,
∴△AFD∽△ABC.”
乙同学的解答正确吗?若不正确,请你改正.
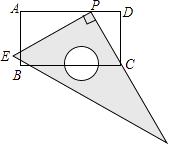
 25. 如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E.
25. 如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E.请问:△CDP与△PAE相似吗?如果相似,请写出证明过程.
-