初中数学青岛版九年级上学期 第1章 1.1相似多边形
试卷更新日期：2020-08-07 类型：同步测试
一、单选题
-
1. 下列说法正确的是（ ）
A、菱形都是相似图形 B、各边对应成比例的多边形是相似多边形 C、等边三角形都是相似三角形 D、矩形都是相似图形2. 下列图案中花边的内外边缘（每个图形边缘等宽）所围成的图形不相似的是（ ）A、
B、
C、
D、
3. 如果一个矩形对折后所得矩形与原矩形相似，则此矩形的长边与短边的比是（ ）A、1： B、 ：1 C、2：1 D、4：14. 如图所示的两个四边形相似，则α的度数是( )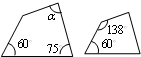
A、60° B、75° C、87° D、120°5. 已知四边形ABCD∽四边形A′B′C′D′，四边形ABCD与四边形A′B′C′D′的周长分别为24、36，则它们对角线AC与A′C′的比为（ ）
A、2：3 B、3：2 C、4：9 D、9：46. 如图所示，在长为8cm，宽为6cm的矩形中，截去一个矩形（图中阴影部分），如果剩下的矩形与原矩形相似，那么剩下矩形的面积是（ ）
A、28cm2 B、27cm2 C、21cm2 D、20cm27. 如果两个相似五边形的面积和等于65cm2 ， 其中一组对应边的长分别为3cm和4.5cm，那么较大五边形的面积为（ ）
A、26cm2 B、39cm2 C、20cm2 D、45cm28. 志远要在报纸上刊登广告，一块10cm×5cm的长方形版面要付广告费180元，他要把该版面的边长都扩大为原来的3倍，在每平方厘米版面广告费相同的情况下，他该付广告费（ ）
A、540元 B、1080元 C、1620元 D、1800元9. 如图，取一张长为a，宽为b的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边a、b应满足的条件是（ ）
A、a= b B、a=2b C、a=2 b D、a=4b10. 如图，已知矩形ABCD中，AB=1，在BC上取一点E，沿AE将△ABE向上折叠，使B点落在AD上的F点，若四边形EFDC与矩形ABCD相似，则AD= （ ）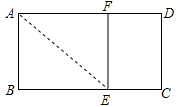
A、
B、
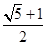C、
D、2
二、填空题
-
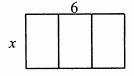
11. 一个四边形的边长分别是3，4，5，6，另一个与它相似的四边形最小边长为6，则另一个四边形的最长边是.12. 在一张比例尺为1：50000的地图上，如果一块多边形地的周长是320cm，那么这块地的实际周长是km.13. 在比例尺为1：10000的地图上，一块面积为2平方厘米的区域表示的实际面积为平方米。14. 矩形的两边长分别为 和6（ ），把它按如图方式分割成三个全等的小矩形，每一个小矩形与原矩形相似，则 .
15. 如图，正方形ABCD中，点E是对角线BD上的一点，BE=BC，过点E作EF⊥AB，EG⊥BC，垂足分别为点F，G，则正方形FBGE与正方形ABCD的相似比为 ．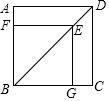
16. 如图，正方形 的边长是 ，除 和 四点外，图形的其他顶点均为所在的一条线段的中点，则从正方形 中挖掉阴影部分后，所剩下部分面积等于 ．
三、作图题
-
17. 如图，左边格点图中有一个四边形，请在右边的格点图中画出一个与该四边形相似的图形，要求大小与左边四边形不同．
四、解答题
-
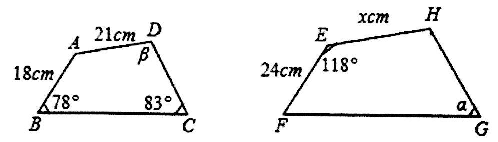
18. 如图，四边形ABCD∽四边形EFGH，求∠α、∠β的大小和EH的长度．
19. 图中所示为两幅形状相似的油画A和B，它们的对角线分别长42cm和48cm．问油画A的面积是油画B的百分之几？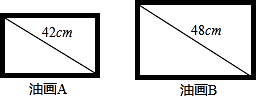
20. 若四边形ABCD与四边形A1B1C1D1相似，相似比为k1= ，又四边形A1B1C1D1与四边形A2B2C2D2相似，相似比为k2= ，请问四边形ABCD与四边形A2B2C2D2相似吗？若相似，相似比是多少？
21. 已知四边形ABCD与四边形A1B1C1D1相似，且A1B1：B1C1：C1D1：D1A1=7：8：11：14，若四边形ABCD的周长为40，求四边形ABCD各边的长．
-
