浙江省杭州市2019-2020学年高一下学期数学教学质量检测试卷
试卷更新日期:2020-08-07 类型:月考试卷
一、单选题
-
1. 设集合 , ,则 ( )A、 B、 C、 D、2. 函数f(x)=log3(2﹣x)的定义域是( )A、[2,+∞) B、(2,+∞) C、(﹣∞,2) D、(﹣∞,2]3. 已知幂函数 在第一象限内的图象如图所示.若 则与曲线 , , , 对应的n的值依次为( )
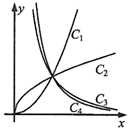 A、 B、 C、 D、4. 要得到函数 的图象,只需将函数 的图象( )A、向左平移 B、向右平移 C、向左平移 D、向右平移5. 已知向量 , .若 ,则 ( )A、 B、 C、 D、6. 已知 ,且 ,则 ( )A、 B、 C、 D、7. 若 是公差不为 的等差数列,满足 ,则该数列的前8项和 ( )A、-10 B、-5 C、0 D、58. 如图,点 在圆 上,且点 位于第一象限,圆 与 正半轴的交点是 ,点 的坐标为 , ,若 则 的值为( )
A、 B、 C、 D、4. 要得到函数 的图象,只需将函数 的图象( )A、向左平移 B、向右平移 C、向左平移 D、向右平移5. 已知向量 , .若 ,则 ( )A、 B、 C、 D、6. 已知 ,且 ,则 ( )A、 B、 C、 D、7. 若 是公差不为 的等差数列,满足 ,则该数列的前8项和 ( )A、-10 B、-5 C、0 D、58. 如图,点 在圆 上,且点 位于第一象限,圆 与 正半轴的交点是 ,点 的坐标为 , ,若 则 的值为( ) A、 B、 C、 D、9. 若不等式 对任意实数x恒成立,则 ( )A、-1 B、0 C、1 D、210. 已知平面向量 , , ,对任意实数x,y都有 , 成立.若 ,则 的最大值是( )A、 B、 C、 D、
A、 B、 C、 D、9. 若不等式 对任意实数x恒成立,则 ( )A、-1 B、0 C、1 D、210. 已知平面向量 , , ,对任意实数x,y都有 , 成立.若 ,则 的最大值是( )A、 B、 C、 D、二、双空题
-
11. 向量 , ,且 ,则 , .12. 函数 的部分图像如图所示.若 (点A为图像的一个最高点), ,则 , .
 13. 已知 是定义在R上的奇函数,当 时 (m为常数),则 , .
13. 已知 是定义在R上的奇函数,当 时 (m为常数),则 , .三、填空题
-
14. 有一扇形其弧长为6,半径为3,则该弧所对弦长为 扇形面积为15. 在数列 中, , ,且数列 为等比数列,则 .16. 如图,在边长为1的正方形ABCD中,P,Q分别在边BC,CD上,且 ,则 的大小为 .
 17. 已知函数 ,若函数 恰有2个不同的零点,则实数 的取值范围为 .
17. 已知函数 ,若函数 恰有2个不同的零点,则实数 的取值范围为 .四、解答题
-
18. 设集合 , .
(Ⅰ)若 ,求实数 的值;
(Ⅱ)若 ,求实数a的取值范围.
19. 已知函数 , .(1)、求 的最大值和最小值;(2)、若不等式 在 上恒成立,求实数m的取值范围.