2021高考一轮复习第十六讲三角函数的图象与性质

试卷更新日期：2020-08-07 类型：一轮复习

进入出卷网下载

一、单选题

1. 将函数 $f (x) = \sin 2 x$ 的图象向右平移 $\frac{π}{6}$ 个单位得到 $g (x)$ ，下列关于 $g (x)$ 的说法正确的是（）

A、 $x = \frac{π}{12}$ 是对称轴 B、在 $[0 ， \frac{π}{2}]$ 上单调递增 C、在 $[0 ， \frac{π}{3}]$ 上最大值为1 D、在 $[- \frac{π}{3} ， 0]$ 上最小值为 $- 1$

查看试题解析
2. 已知函数 $f (x) = \sin ω x + \sqrt{3} \cos ω x (ω > 0)$ 的图象关于直线 $x = \frac{π}{8}$ 对称，则 $ω$ 的最小值为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{4}{3}$ D、 $\frac{8}{3}$

查看试题解析
3. 已知函数 $y = \sin (ω x + \frac{π}{3}) (ω > 0)$ 在区间 $(- \frac{π}{6} ， \frac{π}{3})$ 上单调递增，则 $ω$ 的取值范围是（）

A、 $(0 ， \frac{1}{2}]$ B、 $[\frac{1}{2} ， 1]$ C、 $(\frac{1}{3} ， \frac{2}{3}]$ D、 $[\frac{2}{3} ， 2]$

查看试题解析
4. 已知函数 $f (x) = \cos \frac{x}{2} - \sqrt{3} \sin \frac{x}{2}$ 的图象为C，为了得到关于原点对称的图象，只要把C上所有的点（）

A、向左平移 $\frac{π}{3}$ 个单位 B、向左平移 $\frac{2 π}{3}$ 个单位 C、向右平移 $\frac{π}{3}$ 个单位 D、向右平移 $\frac{2 π}{3}$ 个单位

查看试题解析
5. 函数 $f (x) = 2 sin (w x + φ) (w > 0 ， x \in R)$ 的部分图象如图所示，则该函数图象的一个对称中心是（）

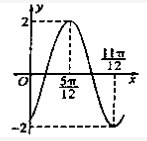A、 $(\frac{π}{3} ， 0)$ B、 $(- \frac{2 π}{3} ， 0)$ C、 $(- \frac{4 π}{3} ， 0)$ D、 $(\frac{4 π}{3} ， 0)$

查看试题解析
6. 下列函数中，周期为1的奇函数是（）

A、y=1-2sin²πx B、y=sin $(2 πx + \frac{π}{3})$ C、y=tan $\frac{π}{2}$ x D、y=sinπxcosπx

查看试题解析
7. 下列函数中，最小正周期为π的偶函数是（）

A、 $y = \sin 2 x$ B、 $y = \cos \frac{x}{2}$ C、 $\sin 2 x + \cos 2 x$ D、 $y = \frac{1 - \tan^{2} x}{1 + \tan^{2} x}$

查看试题解析
8. 已知函数 $f (x) = \sqrt{3} \sin (2 x + φ) + \cos (2 x + φ)$ 为R上的奇函数，且在 $[\frac{π}{4} ， \frac{π}{2}]$ 上单调递增，则 $φ$ 的值可能是（）

A、 $- \frac{2 π}{3}$ B、 $- \frac{π}{6}$ C、 $\frac{π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
9. 函数 $y = \sin (2 x + \frac{π}{4})$ 的最小正周期是（）

A、 $π$ B、 $2 π$ C、 $\frac{π}{2}$ D、 $\frac{π}{4}$

查看试题解析
10. 函数 $f (x) = \cos x (1 + \sqrt{3} \tan x)$ 的最小正周期为（）

A、 $2 π$ B、 $π$ C、 $\frac{3}{2} π$ D、 $\frac{1}{2} π$

查看试题解析
11. 函数 $y = {cos}^{2} x + sin x - 1$ 的值域为（）

A、 $(- \infty, \frac{1}{4}]$ B、 $[0, \frac{1}{4}]$ C、 $[- 2, \frac{1}{4}]$ D、 $[- 2, 0]$

查看试题解析
12. 把函数 $y = \sin (x + \frac{π}{6})$ 图象上各点的横坐标伸长为原来的2倍，纵坐标不变，再将图象向右平移 $\frac{π}{3}$ 个单位，那么所得图象的一个对称中心为（）

A、 $(\frac{π}{3} ， 0)$ B、 $(\frac{π}{4} ， 0)$ C、 $(\frac{π}{12} ， 0)$ D、 $(0 ， 0)$

查看试题解析

二、多选题

13. 函数f（x）＝cos（2x $+ \frac{π}{6}$ ）的图象的一条对称轴方程为（）

A、x = $\frac{π}{6}$ B、x= $\frac{5 π}{12}$ C、x = $\frac{11 π}{12}$ D、x= $- \frac{2 π}{3}$

查看试题解析
14. 将函数 $f (x) = \sqrt{3} \cos (2 x + \frac{π}{3}) - 1$ 的图象向左平移 $\frac{π}{3}$ 个单位长度，再向上平移1个单位长度，得到函数 $g (x)$ 的图象，则下列关于函数 $g (x)$ 的说法正确的是（）

A、最大值为 $\sqrt{3}$ ，图象关于直线 $x = \frac{π}{12}$ 对称 B、图象关于y轴对称 C、最小正周期为 $π$ D、图象关于点 $(\frac{π}{4} ， 0)$ 对称

查看试题解析

三、填空题

15. 若函数 $f (x) = 2 \sin (2 x + φ) (0 < φ < \frac{π}{2})$ 的图象过点 $(0 ， \sqrt{3})$ ，则函数 $f (x)$ 在 $[0 ， π]$ 上的单调减区间是．

查看试题解析
16. 函数 $f (x) = 2 \sin (2 x - \frac{π}{6}) - m$ ，若 $f (x) \leq 0$ 在 $x \in [0 ， \frac{π}{2}]$ 上恒成立，则m的取值范围是；若 $f (x)$ 在 $x \in [0 ， \frac{π}{2}]$ 上有两个不同的解，则m的取值范围是.

查看试题解析
17. 不等式 $\sin^{2} x - \cos^{2} x \geq 0$ 的解集为．

查看试题解析

四、解答题

18. 已知函数 $f (x) = \sin x - 2 \sqrt{3} \cos^{2} \frac{x}{2} + \sqrt{3}$

(1)、求 $f (π)$ 的值；

(2)、求函数 $y = | f (x) |$ 的单调递增区间.

查看试题解析
19. 已知函数 $f (x) = 2 \sqrt{3} {cos}^{2} x + sin (π - 2 x)$ ．

(1)、求函数 $f (x)$ 的最小正周期．

(2)、求函数 $f (x)$ 在 $[0 ， \frac{π}{2}]$ 上的单调区间．

查看试题解析
20. 已知函数 $f (x) = \sin x \cos x + \frac{\sqrt{3}}{2} (\cos^{2} x - \sin^{2} x)$ .

(1)、求 $f (\frac{π}{6})$ 的值；

(2)、求 $f (x)$ 的单调递增区间；

(3)、求 $f (x)$ 的最大值.

查看试题解析

2021高考一轮复习 第十六讲 三角函数的图象与性质

一、单选题

二、多选题

三、填空题

四、解答题

2021高考一轮复习第十六讲三角函数的图象与性质