广东省揭阳市2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期：2020-08-06 类型：期末考试
一、选择题（本大题10小题，每小题3分，共30分.）
-
1. 下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 已知三角形的三边长分别为2、x、3，则x可能是（ ）A、1 B、4 C、5 D、63. 一本笔记本5元，买x本共付y元，则5和y分别是（ ）A、常量，常量 B、变量，变量 C、常量，变量 D、变量，常量4. （π-3.14）0+（ ）-2=（ ）A、5 B、-3 C、 D、5. 袋子中装有10个黑球、1个白球，它们除颜色外无其他差别，随机从袋子中摸出一个球，则（ ）A、这个球一定是黑球 B、摸到黑球、白球的可能性的大小一样 C、这个球可能是白球 D、事先能确定摸到什么颜色的球6. 如图，直线AB//CD，EF分别与AB、CD交于G、H，∠1=55°，则∠2的度数为（ ）
A、105° B、115° C、125° D、135°7. 下列说法错误的是（ ）A、对顶角一定相等 B、在同一平面内，有且只有一条直线和已知直线垂直 C、同位角相等，两直线平行 D、如果两个角的和是90°，那么称这两个角互为余角8. 如图，△ABC中，AB=AC，D是BC中点，下列结论中不正确的是（ ）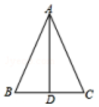
A、AB=2BD B、AD⊥BC C、AD平分∠BAC D、∠B=∠C9. 下列各图中，a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（ ）
A、甲和乙 B、只有乙 C、甲和丙 D、乙和丙10. 下列图案由边长相等的黑、白两色正方形按一定的规律拼接而成，依此规律，第n个图形中白色正方形的个数为（ ）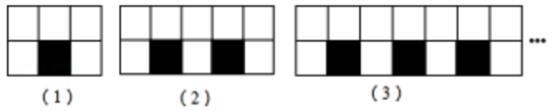
A、4n+1 B、4n-1 C、3n-2 D、3n+2二、填空题（本大题7小题，每小题4分，共28分）
-
11. 某红外线波长为0.00 000 094米，数字0.00 000 094用科学记数法表示为12. 计算：（2x-y）（x-3y）=13. 如图，点P是∠AOB平分线OC上一点，PD⊥OB，垂足为D，若PD=2，则点P到边OA的距离是
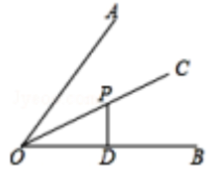14. 如图，△ABC与△A'B'C'关于直线l对称，且∠A=105°，∠C'=30°，则∠B的度数为
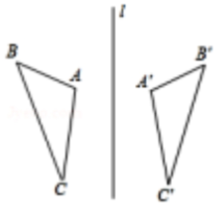15. 如图，三角形ABC的高AD=4，BC=6，点E在BC上运动，若设BE的长为 三角形ACE的面积为y，则y与x的关系式为.
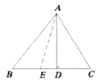16. 若m（m-2）=3，则（m-1）²的值是17. 如图，△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于D.给出下列结论：
⑴∠AFC=∠AFE
⑵BF=DE
⑶∠BFE=∠BAE
⑷∠BFD=∠CAF.
其中正确的结论是（填写所正确结论的序号），
三、解答题（一）（本大题共3小题，每小题6分，共18分）
-
18. 计算：（-2x²）²+x3·x-x5÷x19. 先化简，再求值：
（a²b+2ab²）÷b+（a-b）²，其中a=-1，b=-2.
20. 把下面的推理过程补充完整，并在括号内注明理由.
已知：如图，BC//EF，AB=DE，BC=EF，试说明∠C=∠F.
解：∵.BC//EF（已知）
∴∠ABC= ▲ （ ▲ ）
在△ABC与△DEF中
∴△ABC≌△DEF（ ▲ ）
∴∠C=∠F（ ▲ ）
四、解答题（二）（本大题共3小题，每小题8分，共24分）
-
21. 如图，在△ABC中，∠C=90°，PD=PA，
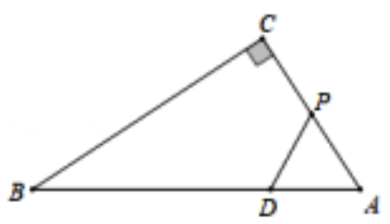(1)、尺规作图：作BD的垂直平分线交BC于点E，垂足为点F（不写作法，但需保留作图痕迹）；(2)、在（1）所作的图中，连接DE，试说明：DE⊥DP.
22. 某商场的一次促销活动规定：凡在本商场购物，可转动转盘一次，并根据所转结果的折扣付账.
(1)、分别求出打九折，打八折的概率；(2)、求不打折的概率：(3)、小华和小明分别购买了价值200元的商品，活动后他们一共付钱360元，请直接写出他们获得优惠可能的情况.23. 图书馆与学校相距600m，明明从学校出发步行去图书馆，亮亮从图书馆骑车去学校两人同时出发，匀速相向而行，他们与学校的距离S（m）与时间t（s）的图象如图所示：根据图象回答：
(1)、明明步行的速度为mls； 亮亮骑车的速度为m/s.(2)、分別写出明明、亮亮与学校的距离S1、S2与时间!的关系式；(3)、求a的值.五、解答题（本大题共2小题，每小题10分，共20分）
-
24. 阅读下列学习材料并解决问题
定义：如果一个数i的平方等于一1，记为i2=-1，这个数i叫做虚数单位，它的加，减，乘法运算与整式的加，减，乘法运算类似，例如计算：
（2+i）+（3-4i）=5-3i，
（2+i）-（3-4i）=-1+5i
（2+i）（3-4i）=6-8i+3i-4i2=10-5i.
(1)、填空：i3=；i4=(2)、计算：①（2+i）（2-i）：②（2+i）²：(3)、试一试：请利用以前学习的有关知识将 化简成a+bi的形式（即分母不含i的形式）25. 如图，在△ABC中，BC=7，高线AD、BE相交于点O，且AE=BE.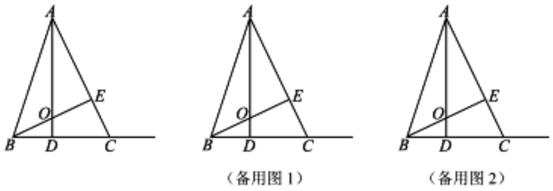
(1)、∠ACB与∠AOB的数量关系是(2)、试说明：△AEO≌△BEC；(3)、点F是直线AC上的一点且CF=BO，动点P从点O出发，沿线段OA以每秒1个单位长度的速度向终点A运动，动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动，P、Q两点同时出发，当点P到达A点时，P、Q两点同时停止运动。设点P的运动时间为t秒，问是否存在t值，使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等?若存在，请在备用图中画出大致示意图，并直接写出符合条件的t值：若不存在，请说明理由.