江苏省海安市八校2019-2020学年七年级下学期数学6月月考试卷

试卷更新日期：2020-08-06 类型：月考试卷

进入出卷网下载

一、单选题

1. 在 $\frac{π}{2}$ ， $\frac{1}{7}$ ， $\sqrt{5}$ ， $- \sqrt[3]{27}$ ，6.1010010001…，3.14中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 2017年中考已经结束，南平市教研室从各校随机抽取1000名考生的数学试卷进行调査分析，这个问题的样本容量是（）

A、 1000 B、1000名 C、1000名学生 D、1000名考生的数学试卷

查看试题解析
3. 有下列五个命题：①过一点有且只有一条直线与已知直线平行； ②平行于同一条直线的两条直线互相平行；③过一点有且只有一条直线与已知直线垂直； ④垂直于同一条直线的两条直线互相平行；⑤三角形的一个外角等于它的两个内角的和.其中真命题的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 若一个多边形的外角和与它的内角和相等，则这个多边形是（）

A、三角形 B、四边形 C、五边形 D、六边形

查看试题解析
5. 篮球比赛规定：胜一场得3分，负一场得1分.某篮球队进行了6场比赛，得了14分，该队获胜的场数是（）

A、2 B、3 C、4 D、5

查看试题解析
6. 若 $x^{| 2 m - 3 |} + (m - 2) y = 6$ 是关于x、y的二元一次方程，则m的值是（）

A、1或2 B、1 C、2 D、3

查看试题解析
7. 对于任意实数m，点P（m﹣1，9﹣3m）不可能在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 等腰三角形的面积为24平方厘米，腰长8厘米.在底边上有一个动点P，则P到两腰的距离之和为（）

A、4cm B、6cm C、8cm D、10cm

查看试题解析
9. 下图是南通市1995-2001年国内生产总值增长率变化情况，下列结论不正确的是（）

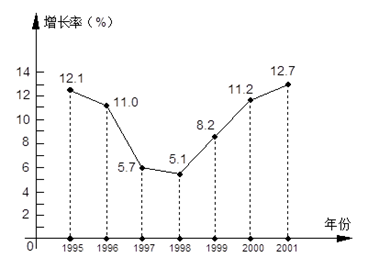A、1995-1998年，南通市国内生产总值的年增长率逐年减小 B、自1998年以来，南通市国内生产总值的年增长率开始回升 C、1995年-2001年，南通市每年的国内生产总值有增有减 D、1995年-2001年，南通市每年的国内生产总值不断增长

查看试题解析
10. 一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后接着按图中箭头所示方向跳动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，且每秒跳动一个单位，那么第 2020 秒时跳蚤所在位置的坐标是（）

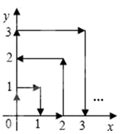A、（5，44） B、（4，44） C、（4，45） D、（5，45）

查看试题解析

二、填空题

11. 已知点P（m+1，2m-1）在x轴上，则P的坐标是.

查看试题解析
12. 一个正多边形的每个内角度数均为135°，则它的边数为.

查看试题解析
13. 若 ${\begin{array}{l} x = 3 - m \\ y = 2 m + 1 \end{array}$ ，则x与y之间的关系为.

查看试题解析
14. △ABC中，AD是BC边上的高，∠BAD=50°，∠CAD=20°，则∠BAC=.

查看试题解析
15. 如图，BD∥CE，∠1=85°，∠2=37°，则∠A=°.

查看试题解析
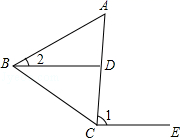16. 如图，三角形纸片ABC中∠A=63°，∠B=77°，将纸片一角折叠，使点C落在△ABC的内部，若∠2=50°，则∠1=.

查看试题解析
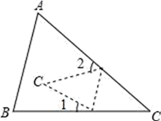17. 已知关于x的不等式组 ${\begin{matrix} x - a \geq 0 \\ 5 - 2 x > 1 \end{matrix}$ 只有四个整数解，则实数a的取值范是．

查看试题解析
18. 设 $[x)$ 表示大于 $x$ 的最小整数，如 $[3) = 4$ ， $[- 1.2) = - 1$ ，下列4个结论：① $[0) = 0$ ；② $[x) - x$ 的最小值是0；③ $[x) - x$ 的最大值是1； ④存在实数 $x$ ，使 $[x) - x = 0.5$ 成立.其中正确的是.（填序号）

查看试题解析

三、解答题

19.

(1)、计算： $| \sqrt{3} - 2 | + \sqrt{{(- 2)}^{2}} - \sqrt[3]{64}$ ；

(2)、解方程： $4 {(x + 1)}^{2} - 3 = 6$ ；

(3)、解方程组： ${\begin{array}{l} 3 x - 5 y = - 3 \\ - 4 x + 10 y = 6 \end{array}$ ；

(4)、解不等式组： ${\begin{array}{l} x - \frac{3}{2} (2 x - 1) \leq 4 \\ \frac{1 + 3 x}{2} > 2 x - 1 \end{array}$ .

查看试题解析
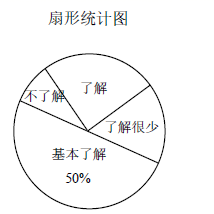
20. 已知 $a 、 b$ 满足 $b = \frac{\sqrt{a^{2} - 4} + \sqrt{4 - a^{2}} + 4}{a - 2}$ ，求 $\sqrt{a - 6 b}$ 的平方根.

查看试题解析
21. “校园安全”受到全社会的广泛关注.某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图.请根据统计图中所提供的信息解答下列问题：

(1)、接受问卷调查的学生共有人；

(2)、扇形统计图中“了解”部分所对应扇形的圆心角为度；

(3)、请补全条形统计图；

(4)、若该中学共有学生1200人，则该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数约为多少人？

查看试题解析
22. 在解方程组 ${\begin{array}{l} a x - b y = 13 \\ c x - y = 4 \end{array}$ 时，甲同学因看错了 $b$ 的符号，从而求得解为 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ 乙同学因看漏了 $c$ ，从而求得解为 ${\begin{array}{l} x = 5 \\ y = 1 \end{array}$ 试求 $a, b, c$ 的值.

查看试题解析
23. 如图， $A E$ 为 $∠ B A D$ 的角平分线， $C F$ 为 $∠ B C D$ 的角平分线，且 $A E / / C F$ ，求证： $∠ B = ∠ D$ .

查看试题解析
24. 现计划把甲种货物306吨和乙种货物230吨运往某地，已知有A、B两种不同规格的货车共50辆，如果每辆A型货车最多可装甲种货物7吨和乙种货物3吨，每辆B型货车最多可装甲种货物5吨和乙种货物7吨.

(1)、装货时如何安排A、B两种货车的辆数，共有哪些方案？

(2)、使用A型车每辆费用为600元，使用B型车每辆费用800元，上述方案中，哪个方案运费最省？最省的运费是多少元？

查看试题解析
25. 在 $Rt △ ABC$ 中， $∠ C = 90 °$ ，点 $D$ ， $E$ 分别是边 $AC$ ， $BC$ 上的点，点 $P$ 是一动点.记 $∠ PDA$ 为 $∠ 1$ ， $∠ PEB$ 为 $∠ 2$ ， $∠ DPE$ 为 $∠ α$ .

(1)、若点 $P$ 在线段 $AB$ 上，且 $∠ α = 50 °$ ，如图1，则 $∠ 1 + ∠ 2 =$ ；

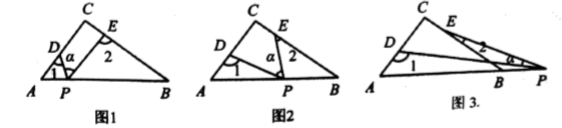(2)、若点 $P$ 在边 $AB$ 上运动，如图2所示，请猜想 $∠ α$ ， $∠ 1$ ， $∠ 2$ 之间的关系，并说明理由；

(3)、若点 $P$ 运动到边 $AB$ 的延长线上，如图3所示，则 $∠ α$ ， $∠ 1$ ， $∠ 2$ 之间又有何关系？请直接写出结论，不用说明理由.

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，对于点 $A (x ， y)$ ，若点 $B$ 的坐标为 $(a x + y ， x + a y)$ ，则称点是的“ $a - a$ 演化点”.例如，点 $A (- 2 ， 6)$ 的“ $\frac{1}{2} - \frac{1}{2}$ 演化点”为 $B (\frac{1}{2} \times (- 2) + 6 ， - 2 + \frac{1}{2} \times 6)$ ，即 $B (5 ， 1)$ .

(1)、已知点 $P (- 1 ， 5)$ 的“ $3 - 3$ 演化点”是 $P_{1}$ ，则 $P_{1}$ 的坐标为；

(2)、已知点 $T (6 ， 0)$ ，且点 $Q$ 的“ $2 - 2$ 演化点”是 $Q_{1} (4 ， 8)$ ，则 $Δ Q T Q_{1}$ 的面积 $S_{Δ Q T Q_{1}}$ 为；

(3)、已知 $O (0 ， 0)$ ， $A (0 ， 8)$ ， $C (5 ， 0)$ ， $D (3 ， 8)$ ，且点 $K (1 ， - k)$ 的“ $k - k$ 演化点”为 $K_{1}$ ，当 $S_{Δ K_{1} A D} = S_{Δ K_{1} O C}$ 时， $k =$ .

查看试题解析