浙江省绍兴市柯桥区钱清学区2019-2020学年八年级下学期数学6月月考试卷

试卷更新日期：2020-08-06 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列计算结果正确的是（）

A、 $\sqrt{2}$ ＋ $\sqrt{5}$ ＝ $\sqrt{7}$ B、3 $\sqrt{2}$ － $\sqrt{2}$ ＝3 C、 $\sqrt{2}$ × $\sqrt{5}$ ＝ $\sqrt{10}$ D、 $\frac{\sqrt{2}}{\sqrt{5}}$ ＝5 $\sqrt{10}$

查看试题解析
2. 在下列图形中，既是中心对称又是轴对称的图形是（）

A、 B、 C、 D、

查看试题解析
3. 下列关于x的一元二次方程中，有两个不相等的实数根的方程是（）

A、 $x^{2} + 1 = 0$ B、 $9 x^{2} - 6 x + 1 = 0$ C、 $x^{2} - x + 2 = 0$ D、 $x^{2} - 2 x - 2 = 0$

查看试题解析
4.
如图，已知∠1=∠2，AC=AD，增加下列条件：①AB=AE；②BC=ED；③∠C=∠D；④∠B=∠E．其中能使△ABC≌△AED的条件有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
5. 若一个多边形的内角和小于其外角和,则这个多边形的边数是（）

A、3 B、4 C、5 D、6

查看试题解析
6. 某校对初中学生开展的四项课外活动进行了一次抽样调查（每人只参加其中的一项活动），调查结果如图所示，根据图形所提供的样本数据，可得学生参加科技活动的频率是（　　）

A、0.15 B、0.2 C、0.25 D、0.3

查看试题解析
7. 下列三角形纸片，能沿直线剪一刀得到等腰梯形的是（）

A、 B、 C、 D、

查看试题解析
8. 如图，菱形ABCD中，∠BAD=60°，M是AB的中点，P是对角线AC上的一个动点，若PM+PB的最小值是3，则AB长为（）

A、3 B、 $\sqrt{3}$ C、6 D、 $2 \sqrt{3}$

查看试题解析
9. 某种新产品进价是120元，在试销阶段发现每件售价（元）与产品的日销售量（件）始终存在下表中的数量关系：

每件售价（元）

130

150

165

每日销售量（件）

70

50

35

商场经理给该件商品定价为x元时，每日盈利可达到1600元。则可列方程为（）

A、（x-120）（200-x）=1600 B、x（200-x）=1600 C、（x-120）（180-x）=1600 D、x（180-x）=1600

查看试题解析
10. 如图，矩形ABCD的边AB在x轴上，且AB的中点与原点重合，AB=2，AD=1，过定点Q（0，2）和动点P（a，0）的直线与矩形ABCD的边有公共点，则实数a的取值范围是（）.

A、-3 $\leq$ a $\leq$ 2 B、-3 $\leq a$ $\leq 3$ C、 $- 2 \leq a \leq 2$ D、 $- 2 \leq a \leq 3$

查看试题解析

二、填空题

11. 使式子 $\sqrt{4 - x}$ 有意义的x的取值范围是.

查看试题解析
12. 数据2， $x$ ，9，2，8，5的平均数为5，这组数据的极差为.

查看试题解析
13. 用反证法证明命题“在△ABC中，若∠A＞∠B＋∠C，则∠A＞90°”时，应先假设.

查看试题解析
14. 请你写出一个有一根为1的一元二次方程：.

查看试题解析
15.
如图，要测量的A、C两点被池塘隔开，李师傅在AC外任选一点B，连接BA和BC，分别取BA和BC的中点E、F，量得E、F两点间的距离等于23米，则A、C两点间的距离米．

查看试题解析
16. 如图，已知△ABC中，∠B=50°，分别以A，C为圆心，BC，AB长为半径画弧，两弧在直线BC上方交于点D，连接AD，CD，则∠D=.

查看试题解析
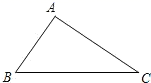17. 已知x²+x-1=0，求2x² +2x-2012= 。

查看试题解析
18. 我们新定义一种三角形，两边平方和等于第三边平方的2倍的三角形叫做奇异三角形，那么“等边三角形一定是奇异三角形”是命题.（填“真”或“假”）

查看试题解析
19. 小宇同学在一次手工制作活动中，先把一张长方形纸片按如图所示的方式进行
折叠，使折痕的左侧部分比右侧部分短 $1 cm$ ；展开后按图的方式再折叠一次，使第二次折痕的左侧部分比右侧部分长 $1 cm$ ，再展开后，在纸上形成的两条折痕之间的距离是 $12$

查看试题解析
20. 如图，正方形ABCD、正方形A₁B₁C₁D₁、正方形A₂B₂C₂D₂均位于第一象限内，它们的边平行于x轴或y轴，其中点A、A₁、A₂在直线OM上，点C、C₁、C₂在直线ON上，O为坐标原点，已知点A的坐标为（3，3），正方形ABCD的边长为1.若正方形A₂B₂C₂D₂的边长为2011，则点B₂的坐标为.

查看试题解析

三、解答题

21.

(1)、先化简，再求值： $(a - \sqrt{3}) (a + \sqrt{3}) - a (a - 6)$ ，其中 $a = \sqrt{5} + \frac{1}{2}$ ；

(2)、解方程：x²+4x-1=0.

查看试题解析
22. 请在所给网格中按下列要求画出图形.

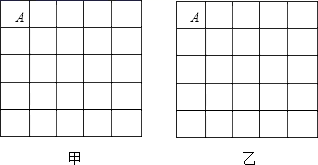(1)、从点A出发画一条线段AB，使它的另一个端点落在格点（即小正方形的顶点，小正方形的边长为1）上，且长度为 $2 \sqrt{2}$

(2)、以（1）中的AB为边的两个四边形，使它们都是中心对称图形且不全等，其顶点都在格点上，各边长都是无理数.（在图乙中画出）

查看试题解析

23. 某中学为了了解七年级男生入学时的跳绳情况，随机选取50名刚入学的男生进行个人一分钟跳绳测试，并以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图（如图所示）.根据图表解答下列问题：

(1)、a= ， b= ；

(2)、这个样本数据的中位数落在第组；

(3)、若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀，则从这50名男生中任意选一人，跳绳成绩为优秀的概率为多少；

(4)、若该校七年级入学时男生共有150人，请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.

组别	次数x	频数（人数）
第1组	50≤x＜70	4
第2组	70≤x＜90	a
第3组	90≤x＜110	18
第4组	110≤x＜130	b
第5组	130≤x＜150	4
第6组	150≤x＜170	2

查看试题解析

24. 两块完全相同的三角板Ⅰ（△ABC）和Ⅱ（△A₁B₁C₁）如图①放置在同一平面上（∠C=∠C₁=90°，∠ABC=∠A₁B₁C₁=60°），斜边重合.若三角板Ⅱ不动，三角板Ⅰ在三角板Ⅱ所在的平面上向右滑动，图②是滑动过程中的一个位置.

(1)、在图②中，连接BC₁、B₁C，求证：△A₁BC₁≌△AB₁C；

(2)、三角板Ⅰ滑到什么位置（点B₁落在AB边的什么位置）时，四边形BCB₁C₁是菱形？说明理由.

查看试题解析
25. 如图是利用四边形的不稳定性制造的一个移动升降装修平台，其基本图形是菱形，主体部分相当于由6个菱形相互连接而成，通过改变菱形的角度，从而可改变装修平台高度.

(1)、如图（1）是一个基本图形，已知AB=1米，当∠ABC为60°时，求AC的长及此时整个装修平台的高度（装修平台的基脚高度忽略不计）；

(2)、当∠ABC从60°变为90°（如图（2）是一个基本图形变化后的图形）时，求整个装修平台升高了多少米.[结果精确到0.1米］

查看试题解析
26. 数学课上，张老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC的中点.∠AEF=90°，且EF交正方形外角∠DCG的角平分线CF于点F，求证：AE=EF.

经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证△AME≌△ECF，所以AE=EF.

在此基础上，同学们作了进一步的研究：

(1)、小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；

(2)、小华提出：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立.你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由.

查看试题解析
27. 如图，把一张长10cm，宽8cm的长方形硬纸板的四周各剪去一个同样大小的正方形，再折合成一个无盖的长方体盒子（纸板的厚度忽略不计）.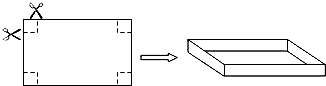

(1)、要使无盖长方体盒子的底面积为48cm² ，那么剪去的正方形的边长为多少？

(2)、如果把长方形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的长方形，然后折合成一个有盖的长方体盒子，那么它的侧面积（指的是高为剪去的正方形边长的长方体的侧面积）可以达到30cm²吗？请说明理由.

查看试题解析

每件售价（元）	130	150	165
每日销售量（件）	70	50	35