江苏省海安市八校2019-2020学年八年级下学期数学6月月考试卷
试卷更新日期:2020-08-06 类型:月考试卷
一、单选题
-
1. 的值等于( )A、 B、 C、 D、2. 在抗击疫情中,某社区志愿者小分队年龄如表:
年龄(岁)
18
22
30
35
43
人数
2
3
2
2
1
则这10名队员年龄的中位数是( )
A、20岁 B、22岁 C、26岁 D、30岁3. 以下列线段的长为三边的三角形中,能构成直角三角形的是( )A、32 , 42 , 52 B、13,5,12 C、 , , D、 , ,4. 一元二次方程2x2+6x+3= 0 经过配方后可变形为( )A、 =6 B、 =12 C、 D、5. 已知y是x的一次函数,下表列出了部分y与x的对应值:x
0
1
2
y
0
2
a
则a的值为( )
A、 B、1 C、3 D、46. 方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定7. 如图,在 的方格中,小正方形的边长是1,点 、 、 都在格点上,则 边上的高为( ) A、 B、 C、 D、8. 已知点 在一次函数 的图像上,且 ,则 的取值范围是( )A、 B、 C、 D、9. 矩形ABCD的边BC上有一动点E,连接AE、DE,以AE、DE为边作▱AEDF.在点E从点B移动到点C的过程中,▱AEDF的面积( )
A、 B、 C、 D、8. 已知点 在一次函数 的图像上,且 ,则 的取值范围是( )A、 B、 C、 D、9. 矩形ABCD的边BC上有一动点E,连接AE、DE,以AE、DE为边作▱AEDF.在点E从点B移动到点C的过程中,▱AEDF的面积( ) A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变10. 在正方形ABCD中,E、F分别为BC、CD边上的两个动点,∠EAF=45°,下列几个结论中:①EF=BE+DF;②MN2=BM2+DN2;③FA平分∠DFE;④连接MF,则△AMF为等腰直角三角形;⑤∠AMN=∠AFE. 其中一定成立的结论有( )A、2个 B、3个 C、4个 D、5个
A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变10. 在正方形ABCD中,E、F分别为BC、CD边上的两个动点,∠EAF=45°,下列几个结论中:①EF=BE+DF;②MN2=BM2+DN2;③FA平分∠DFE;④连接MF,则△AMF为等腰直角三角形;⑤∠AMN=∠AFE. 其中一定成立的结论有( )A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 将直线y=2x-5向上平移2个单位,所得直线解析式为 .12. 若 <0,则代数式 可化简为.13. 如图,一次函数y=kx+b的图象经过点A(0,3),B(4,﹣3),则关于x的不等式kx+b+3<0的解集为.
 14. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根0,则a值为.15. 如图,菱形ABCD中,若BD=8,AC=6,则该菱形的面积为.
14. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根0,则a值为.15. 如图,菱形ABCD中,若BD=8,AC=6,则该菱形的面积为.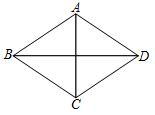 16. 已知 ,则 的值为为.17. 如图,在 中, ,D是AB的中点,若 ,则 的度数为。
16. 已知 ,则 的值为为.17. 如图,在 中, ,D是AB的中点,若 ,则 的度数为。 18. 在平面直角坐标系中,已知直线y x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是.
18. 在平面直角坐标系中,已知直线y x+3与x轴、y轴分别交于A、B两点,点C在线段OB上,把△ABC沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是.三、解答题
-
19. 解方程:(1)、x2+4x﹣1=0;(2)、2(x﹣3)2=x2﹣9.20. 已知 , .(1)、求 的值;(2)、求 的值.21. 已知关于x的一元二次方程mx2-(m+2)x+2=0(m≠0)(1)、求证:方程一定有两个实数根;(2)、若此方程的两根为不相等的整数,求整数m的值.22. 如图中的折线ABC表示某汽车的耗油量y(L/km)与速度x(km/h)之间的函数关系(30≤x≤120).已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
 (1)、当30≤x≤120时,求y与x之间的函数表达式;(2)、该汽车的速度是多少时,耗油量最低?最低是多少.23. 已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.
(1)、当30≤x≤120时,求y与x之间的函数表达式;(2)、该汽车的速度是多少时,耗油量最低?最低是多少.23. 已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.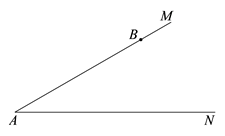 (1)、若△ABC是直角三角形,求AC的长;(2)、若△ABC是等腰三角形,则满足条件的C点有个;(3)、设BC=x,当△ABC唯一确定时,直接写出 的取值范围.24. 如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)、若△ABC是直角三角形,求AC的长;(2)、若△ABC是等腰三角形,则满足条件的C点有个;(3)、设BC=x,当△ABC唯一确定时,直接写出 的取值范围.24. 如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上. (1)、求证:BG=DE;(2)、若E为AD中点,求证:四边形ABGE是平行四边形.
(1)、求证:BG=DE;(2)、若E为AD中点,求证:四边形ABGE是平行四边形.

