江苏省东台市第二联盟2019-2020学年八年级下学期数学6月月考试卷

试卷更新日期：2020-08-06 类型：月考试卷

进入出卷网下载

一、单选题

1. 如果把 $\frac{5 x}{x + y}$ 的x与y都扩大10倍，那么这个代数式的值（）

A、扩大10倍 B、扩大50倍 C、不变 D、缩小到原来的 $\frac{1}{10}$

查看试题解析
2. 对于反比例函数 $y = - \frac{4}{x}$ ，下列说法不正确的是（）

A、图像经过点（1，－4） B、它的图像在第一、三象限 C、当x＞0时，y随x的增大而增大 D、图像关于原点中心对称

查看试题解析
3. 如图，在△ABC中，D是AB上一点，AD＝AC，AE⊥CD，垂足为点E，F是BC的中点，若BD＝16，则EF的长为（）

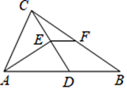A、32 B、16 C、8 D、4

查看试题解析
4. 如图，在菱形ABCD中，AB=BD，点E、F分别在BC、CD上，且BE=CF，连接BF、DE交于点M，延长ED到H使DH=BM，连接AM，AH，则以下四个结论：
①△BDF≌△DCE；②∠BMD=120°；③△AMH是等边三角形；④S_{四边形ABCD}= $\frac{\sqrt{3}}{4}$ AM² ．
其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 在式子 $\sqrt{π}$ ， $\sqrt{a^{2} + b^{2}}$ ， $\sqrt{a + 5}$ ， $\sqrt{- 3 y} （ y \leq 0$ ）, $\sqrt{m^{2} - 1^{}}$ 和 $\sqrt{ab} （ a < 0, b < 0 ）$ 中，是二次根式的有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
6. 如图，菱形ABCD的边长为4，∠DAB=60°，E为BC的中点，在对角线AC上存在一点P，使△PBE的周长最小，则△PBE的周长的最小值为 (　 )

A、 $2 \sqrt{3}$ B、 $4$ C、 $2 \sqrt{3} + 2$ D、 $4 + 2 \sqrt{3}$

查看试题解析
7. 化简 $\sqrt{9 x^{2} - 6 x + 1}$ －（ $\sqrt{3 x - 5}$ ）²的结果是（）

A、6x－6 B、－6x＋6 C、－4 D、4

查看试题解析
8. 正方形ABCD的边AB上有一动点E，以EC为边作矩形ECFG，且边FG过点D，在点E从点A移动到点B的过程中，矩形ECFG的面积（）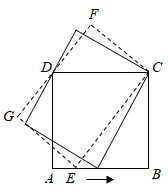

A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变

查看试题解析

二、填空题

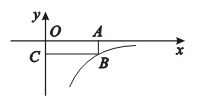
9. 已知点 $A (1, a), B (3, b)$ 都在反比例函数 $y = \frac{4}{x}$ 的图像上，则 $a, b$ 的大小关系为.（用“<”连接）

查看试题解析
10. 如图，面积为3的矩形OABC的一个顶点B在反比例函数 $y = \frac{k}{x}$ 的图象上，另三点在坐标轴上，则 $k =$ .

查看试题解析
11. 当 $m =$ 时，解分式方程 $\frac{x - 5}{x - 3} = \frac{m}{3 - x}$ 会出现增根．

查看试题解析
12. 已知 $a^{2} + b^{2} = 6 a b$ ，且 $a > b > 0$ ，则 $\frac{a + b}{a - b}$ 的值是.

查看试题解析
13. 若 $\sqrt{5}$ 的整数部分是a，小数部分是b，则 $\sqrt{5}$ b $-$ a=.

查看试题解析
14. 如图，在平面直角坐标系中，一条直线与反比例函数y= $\frac{8}{x}$ （x＞0）的图象交于两点A、B，与x轴交于点C，且点B是AC的中点，分别过两点A、B作x轴的平行线，与反比例函数y= $\frac{2}{x}$ （x＞0）的图象交于两点D、E，连接DE，则四边形ABED的面积为．

查看试题解析
15. 为使 $\sqrt{2 x + 4} - \frac{3}{3 x - 6}$ 有意义，x的取值范围是.

查看试题解析
16. 已知a、b、c是△ABC三边的长，且满足关系式 $\sqrt{c^{2} - a^{2} - b^{2}} + | a - b | = 0$ ，
则△ABC的形状为

查看试题解析

三、解答题

17. 如图，正方形网格中的每个小正方形边长都是l，每个小格的顶点叫做格点.以格点为顶点分别按下列要求画图：

(1)、画出一个平行四边形，使其面积为6；

(2)、画出一个菱形，使其面积为4.

(3)、画出一个正方形，使其面积为5.

查看试题解析
18.

(1)、 $(2 \sqrt{6} + 3 \sqrt{5}) (2 \sqrt{6} - 3 \sqrt{5})$ ；

(2)、 $\sqrt{8} + 3 \sqrt{\frac{1}{3}} - \frac{1}{\sqrt{2}} + \frac{\sqrt{3}}{2}$

查看试题解析
19.

(1)、先化简，再求值 $\frac{2}{a - 1} + \frac{a^{2} - 4 a + 4}{a^{2} - 1} \div \frac{a - 2}{a + 1}$ ，其中 $a = 1 + \sqrt{2}$ .

(2)、先化简，再求值 $(\frac{1}{x - y} - \frac{1}{x + y}) \div \frac{2 y}{x^{2} - 2 x y + y^{2}}$ ，其中 $x = 1 + \sqrt{2}$ ， $y = 1 - \sqrt{2}$ .

查看试题解析
20. 关于x的分式方程 $\frac{x}{x + 1} - \frac{a}{x^{2} - 1} = 1$ 的解为负数，求a的取值范围.

查看试题解析
21. 某商场购进甲、乙两种商品，甲种商品共用了20000元，乙种商品共用了24000元.已知乙种商品每件进价比甲种商品每件进价多8元，且购进的甲、乙两种商品件数相同.

(1)、求甲、乙两种商品的每件进价；

(2)、该商场将购进的甲、乙两种商品进行销售，甲种商品的销售单价为60元，乙种商品的销售单价为88元，销售过程中发现甲种商品销量不好，商场决定：甲种商品销售一定数量后，将剩余的甲种商品按原销售单价的七折销售；乙种商品销售单价保持不变.要使两种商品全部售完后共获利不少于24600元，问甲种商品按原销售单价至少销售多少件？

查看试题解析
22. 如图：反比例函数 $y_{1} = \frac{k}{x}$ 的图象与一次函数 $y_{2} = x + b$ 的图象交于 $A$ 、 $B$ 两点，其中 $A$ 点坐标为 $(1 ， 2)$ .

(1)、求反比例函数与一次函数的表达式；

(2)、观察图象，直接写出当 $y_{1} < y_{2}$ 时，自变量 $x$ 的取值范围；

(3)、一次函数的图象与 $y$ 轴交于点 $C$ ，点 $P$ 是反比例函数图象上的一个动点，若 $S_{Δ O C P} = 6$ ，求此时 $P$ 点的坐标.

查看试题解析
23. 为预防传染病，某校定期对教室进行“药熏消毒”．已知药物燃烧阶段，室内每立方米空气中的含药量y(mg)与药物在空气中的持续时间x(min)成正比例；燃烧后，y与x成反比例(如图所示)．现测得药物10分钟燃完，此时教室内每立方米空气含药量为8mg．根据以上信息解答下列问题：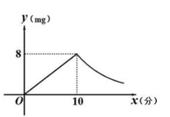

(1)、分别求出药物燃烧时及燃烧后y关于x的函数表达式．

(2)、当每立方米空气中的含药量低于1.6mg时，对人体方能无毒害作用，那么从消毒开始，在哪个时段消毒人员不能停留在教室里?

(3)、当室内空气中的含药量每立方米不低于3.2mg的持续时间超过20分钟，才能有效杀灭某种传染病毒．试判断此次消毒是否有效，并说明理由．

查看试题解析
24. 在矩形ABCD中，AB＝3，BC＝4，E，F是对角线AC上的两个动点，分别从A，C同时出发相向而行，速度均为1cm/s，运动时间为t秒，0≤t≤5.

(1)、AE＝， EF＝

(2)、若G，H分别是AB，DC中点，求证：四边形EGFH是平行四边形.（ $E 、 F$ 相遇时除外）

(3)、在（2）条件下，当t为何值时，四边形EGFH为矩形.

查看试题解析