初中数学人教版八年级上学期 第十二章 全等三角形
试卷更新日期：2020-08-05 类型：单元试卷
一、单选题
-
1. 如图，三条公路两两相交，现计划修建一个油库，要求油库到这三条公路的距离相等，那么选择油库的位置有（ ）处．
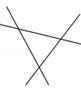A、1 B、2 C、3 D、42. 如图，在△ABC中，∠ACB=90°，BE平分∠ABC，ED⊥AB于点D，若AC=5cm，则AE+DE等于（ ）
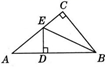A、3cm B、4cm C、5cm D、6cm3. 某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事方法是（ ）
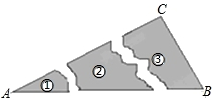A、带①去 B、带②去 C、带③去 D、①②③都带去4. 如图，下列条件中，不能证明 的是（ ）
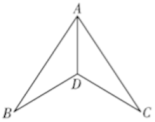A、 ， B、 ， C、 ， D、 ，5. 如图，若△ABC ≌ △ DEF， BC=6， EC=4，则CF的长为 （ ）
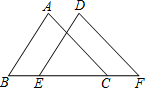A、1 B、2 C、2.5 D、36. 如图，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，连接AC.若AC=8，则四边形ABCD的面积为（ ）
A、32 B、24 C、40 D、367. 如图，△ABC≌△AEF且点F在BC上，若AB=AE，∠B=∠E，则下列结论错误的是（ ）
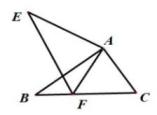A、AC=AF B、∠AFE=∠BFE C、EF=BC D、∠EAB=∠FAC8. 如图，已知∠A=∠B=∠BCD=90 ° ，AB=CD=3，AD=5，BE=10，点C是BE的中点，动点P从点B出发以每秒1个单位的速度沿BC→CD→DA，向终点A运动，设点P的运动时间为t秒.当t为多少秒时，△ABP与△DCE全等（ ）.
A、5 B、3或5 C、3或8 D、5或89. 如图，在△ABC中，∠C=90°，AD平分∠BAC交BC于点D，DE⊥AB于点E，则下列结论：①AD平分∠CDE；②∠BAC=∠BDE；③DE平分∠ADB；④若AC=4BE，则S△ABC=8S△BDE其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个10. 如图，在△ABC中，∠ABC＝45°，F是高AD和BE的交点，CD＝4，则线段DF的长为（ ）
A、3 B、4 C、5 D、6二、填空题
-
11. 如图，在Rt△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC， DC=4cm，则点D到AB的距离为.
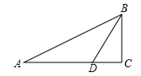12. 如图，已知∠ACD=∠BCE，AC=DC，如果要得到△ACB≌△DCE，那么还需要添加的条件是.（填写一个即可，不得添加辅助线和字母）
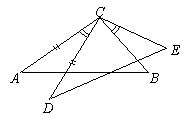13. 工人师傅常用角尺平分一个任意角.做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度分别与M，N重合.则过角尺顶点C的射线OC便是∠AOB的平分线。这样做的依据是.
14. 如图，在△ABC中，∠ACB的平分线交AB于点D，DE⊥AC于点E，F为BC上一点，若DF=AD，△ACD与△CDF的面积分别为10和4，则△AED的面积为。
15. 如图，在△ABC中，BF⊥AC 于点F，AD⊥BC 于点D ，BF 与AD 相交于点E．若AD=BD，BC=8cm，DC=3cm．则 AE= cm ．
16. 如图，在△ABC中，AC=BC，过点A，B分别作过点C的直线的垂线AE，BF，若AE=CF=3，BF=45，则EF=。
17. 如图，在Rt△ABC中，∠C=90°，AC=10，BC=5，PQ=AB，点P和点Q分别在AC和AC
垂线AD上移动，则当AP=时，才能使△ABC和△APQ全等. 
18. 如图，已知在△ABC中，∠A=90°，AB=AC，CD平分∠ACB，DE⊥BC于E，若BC=20cm，则△DEB的周长为cm．
19. 如图， 于E， 于F，若 ， ，则下列结论： ； 平分 ； ； 中正确的是 ．
③④20. 如图，∠AOB=30°，OP平分∠AOB，PD⊥OB于D，PC∥OB交OA于C，若PC=10，则PD= ．
三、解答题
-
21. 如图，有一个池塘，要测池塘两端 ， 的距离，可先在平地上取一个点 ，从点 不经过池塘可以直接达到点 和 ，连接 并延长到点 ，使 ，连接 并延长到点 ，使 ，连接 ，那么量出 的长度就是 ， 的距离，为什么？
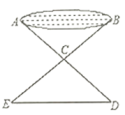22. 如图，D是AB上一点，DF交AC于点E， 试判断AE与CE有怎样的数量关系?并证明你的结论.
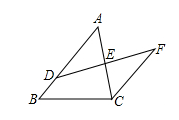23. 如图，在△ABC中，∠1＝∠2，DE∥AC，求证：△ADE是等腰三角形.
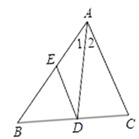24. 如图，∠A=∠D=90°，AC=DB，AC，DB相交于点O，求证：点O在BC的垂直平分线上。
25. 如图，∠A=∠D=90°，BE平分∠ABC，且点E是AD的中点，求证：BC=AB+CD。
26. 如图，等腰△ABC中，∠ACB=90°，AC=BC，点D在AB上，AD=AC，BE垂直于直线CD于点E。
(1)、求∠BCD的度数(2)、求证：CD=2BE(3)、若点O是AB的中点，请直接写出BC、BD、CO三条线段之间的数量关系。27. CD是经过∠BCA顶点C的一条直线，CA=CB，E，F分别是直线CD上两点，且∠BEC=∠CFA=∠α。
(1)、若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：①如图1，若∠BCA=90°，∠α=90°，则BE ▲ CF； EF ▲ |BE-AF|（填“>”，“<”或“=”）；
②如图2，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件，使①中的两个结论仍然成立，并证明两个结论成立；
(2)、如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）。