陕西省渭南市富平县2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-08-05 类型:期末考试
一、选择题:共10个小题,每小题3分,共30分.
-
1. 下列四个图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件为必然事件的是 ( )A、射击一次,中靶 B、12人中至少有2人的生日的在同一个月 C、画一个三角形,其内角和是180° D、掷一枚质地均匀的硬币,正面朝上3. 如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是( )
2. 下列事件为必然事件的是 ( )A、射击一次,中靶 B、12人中至少有2人的生日的在同一个月 C、画一个三角形,其内角和是180° D、掷一枚质地均匀的硬币,正面朝上3. 如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是( )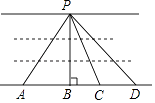 A、PA B、PB C、PC D、PD4. 如图,下列条件能判断 的是( )
A、PA B、PB C、PC D、PD4. 如图,下列条件能判断 的是( ) A、 B、 C、 D、5. 二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.如图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长不足11小时的节气是( )
A、 B、 C、 D、5. 二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.如图是一年中部分节气所对应的白昼时长示意图.在下列选项中白昼时长不足11小时的节气是( )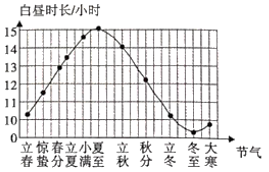 A、惊蛰 B、小满 C、秋分 D、大寒6. 如图,为了估计一池塘岸边两点 之间的距离,小颖同学在池塘一侧选取了一点P,测得 ,那么点A与点B之间的距离不可能是 ( )
A、惊蛰 B、小满 C、秋分 D、大寒6. 如图,为了估计一池塘岸边两点 之间的距离,小颖同学在池塘一侧选取了一点P,测得 ,那么点A与点B之间的距离不可能是 ( )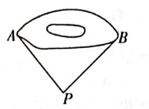 A、 B、 C、 D、7. 如图,若 与 关于直线 对称, 交 于点O,则下列说法不一定正确的是 ( )
A、 B、 C、 D、7. 如图,若 与 关于直线 对称, 交 于点O,则下列说法不一定正确的是 ( )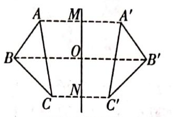 A、 B、 C、 D、8. 某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )
A、 B、 C、 D、8. 某地区用电量与应缴电费之间的关系如下表:则下列叙述错误的是( )用电量(千瓦•时)
1
2
3
4
…
应缴电费(元)
0.55
1.10
1.65
2.20
…
A、用电量每增加1千瓦•时,电费增加0.55元 B、若用电量为8千瓦•时,则应缴电费4.4元 C、若应缴电费为2.75元,则用电量为6千瓦•时 D、应缴电费随用电量的增加而增加9. 如图,把一张上下两边平行的纸条沿 折叠,若 ,则 的度数为( )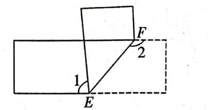 A、48° B、84° C、24° D、96°10. 如图,在 中, 的垂直平分线 交 于点D,连接 ,若 ,则 的度数为 ( )
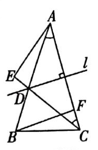
A、48° B、84° C、24° D、96°10. 如图,在 中, 的垂直平分线 交 于点D,连接 ,若 ,则 的度数为 ( ) A、90° B、95° C、105° D、115°
A、90° B、95° C、105° D、115°二、填空题:共4小题,每小题3分,满分12分
-
11. 一个氢原子的直径约为 ,将 用科学记数法表示为.12. 计算: .13. 如图所示的钻石型网格(每个小三角形都相同),假设可以随意在图中取点,那么这个点取在阴影部分的概率为.
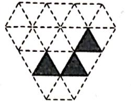 14. 如图,已知在 中, , 平分 ,且 , ,则 °.
14. 如图,已知在 中, , 平分 ,且 , ,则 °.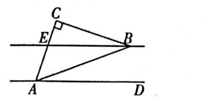
三、解答题:共11小题,共78分.
-
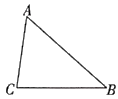
15. 计算: .16. 如图,在 中,尺规作图:作 的角平分线 .(不写作法,保留作图痕迹)
 17. 如图,4×5的方格纸中,请你在除阴影之外的方格中任意选择一个涂黑,使得图中阴影部分构成的图形是轴对称图形.
17. 如图,4×5的方格纸中,请你在除阴影之外的方格中任意选择一个涂黑,使得图中阴影部分构成的图形是轴对称图形. 18. 一个不透明口袋中装有6个红球、9个黄球、3个绿球,这些球颜色外没有任何区别,从中任意摸出一个球.(1)、求摸到绿球的概率;(2)、求摸到红球或绿球的概率.19. 先化简,再求值: ,其中 .20. 如图, 两点分别位于一个假山的两端,小明想用绳子测量 间的距离:现在地上取一个可以直接到达A点和B点的点C,连接 并延长到点D,使 ,连接 并延长到点E,使 ;连接 并测量出它的长度. ,求 的长度.
18. 一个不透明口袋中装有6个红球、9个黄球、3个绿球,这些球颜色外没有任何区别,从中任意摸出一个球.(1)、求摸到绿球的概率;(2)、求摸到红球或绿球的概率.19. 先化简,再求值: ,其中 .20. 如图, 两点分别位于一个假山的两端,小明想用绳子测量 间的距离:现在地上取一个可以直接到达A点和B点的点C,连接 并延长到点D,使 ,连接 并延长到点E,使 ;连接 并测量出它的长度. ,求 的长度.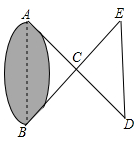 21. 如图, 平分 交 于点D, 于点E, 于点F, ,若 ,求 的长.
21. 如图, 平分 交 于点D, 于点E, 于点F, ,若 ,求 的长.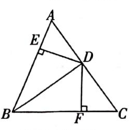 22. 如图,在一个半径为 的圆面上,从中心挖去一个小圆面,当挖去小圆的半径 由小变大时,剩下的圆环面积 也随之发生变化.(结果保留 ).
22. 如图,在一个半径为 的圆面上,从中心挖去一个小圆面,当挖去小圆的半径 由小变大时,剩下的圆环面积 也随之发生变化.(结果保留 ).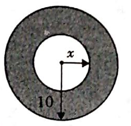 (1)、在这个变化过程中,自变量、因变量各是什么?(2)、求圆环的面积 与 的关系式.(3)、当挖去圆的半径 为 时,剩下圆环面积 为多少?23. 某批乒乓球的质量检验结果如下:
(1)、在这个变化过程中,自变量、因变量各是什么?(2)、求圆环的面积 与 的关系式.(3)、当挖去圆的半径 为 时,剩下圆环面积 为多少?23. 某批乒乓球的质量检验结果如下:抽取的乒乓球数
50
100
150
200
350
400
450
500
优等品的频数
40
96
126
176
322
364
405
450
优等品的频率
0.80
0.96
0.84
0.92
0.90
 (1)、求 的值;(2)、在图中画出这批乒乓球优等品频率的折线统计图;(3)、根据上表,在这批乒乓球中任取一个,它为优等品的概率大约是多少?
(1)、求 的值;(2)、在图中画出这批乒乓球优等品频率的折线统计图;(3)、根据上表,在这批乒乓球中任取一个,它为优等品的概率大约是多少?