陕西省汉中市西乡县2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期：2020-08-05 类型：期末考试
一、选择题（本大题共10小题，每小题3分，共30分）
-
1. 下列手机软件图标中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 生物学家发现一种病毒的长度约为0.0000043米，利用科学记数法表示为（ ）A、4.3×106米 B、4. 3×10﹣5米 C、4.3×10﹣6米 D、43×107米3. 下列计算中，正确的是（ ）A、m2•m3=m6 B、（a2）3=a5 C、（2x）4=16x4 D、2m3÷m3=2m4. 下列事件中，属于必然事件的是（ ）A、一口袋中装有2个红球和1个白球，从中摸出2个球，其中必有一个红球 B、我走出校门，看到的第一辆汽车的牌照的末位数字是偶数 C、抛一枚硬币，正面朝上 D、明天西乡县下雨5. 如图，a∥b，点B在直线b上，且AB⊥BC，若∠1=34°，则∠2的大小为（ ）
A、34° B、54° C、56° D、66°6. 如图表示某加工厂今年前5个月每月生产某种产品的产量c（件）与时间t（月）之间的关系，则对这种产品来说，该厂（ ）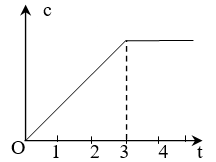
A、1月至3月每月产量逐月增加，4、5两月产量逐月减小。 B、1月至3月每月产量逐月增加，4、5两月产量与3月持平。 C、1月至3月每月产量逐月增加，4、5两月产量均停止生产。 D、1月至3月每月产量不变，4、5两月均停止生产。7. 下列图形中，不一定是轴对称图形的是（ ）A、等腰三角形 B、线段 C、钝角 D、直角三角形8. 作∠AOB的角平分线的作图过程如下，
用下面的三角形全等判定法则解释其作图原理，最为恰当的是（ ）
A、SAS B、ASA C、AAS D、SSS9. 如图，已知∠1＝∠B，∠2＝∠C，则下列结论不成立的是（ ）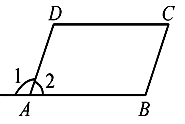
A、∠B＝∠C B、AD∥BC C、∠2＋∠B＝180° D、AB∥CD10. 如图，在四边形ABCD中，∠A=110°，∠B=85°将△BMN沿着MN翻折，得到△FMN，若MF∥AD，FN∥DC，则∠C的度数为（ ）
A、70° B、80° C、90° D、100°二、填空题（本大题共4个小题.每小题3分，共12分）
-
11. 计算 = 。12. 若整式 4x2+Q+1 是完全平方式，请你写出满足条件的单项式Q是。13. 某剧院的观众席的座位为扇形，且按下列方式设置：
排数（x）
1
2
3
4
…
座位数（y）
50
53
56
59
…
写出座位数y与排数x之间的关系式
14. 如图，四边形ABCD中，∠C=40°，∠B=∠D=90°，E、F分别是BC、DC上的一点，当△AEF的周长最小时，∠EAF的度数为。
三、解答题（共78分）
-
15. 计算16. 如图，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A＝32.5°，求∠D的度数。
17. 如图，三角形ABC中，点D在AC上
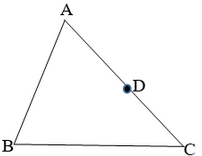(1)、、请你过点D做DE平行BC，交AB于E（要求尺规画图，保留痕迹，不写做法）(2)、如果点E在∠C的平分线上、∠C＝44°那么∠DEC=.18. 口袋里有红球4个、绿球5个和黄球若干个，任意摸出一个球是绿球的概率是 。求：口袋里黄球的个数。
19. 先化简，再求值：[ （x+2y）2-(x+4y )(3x+y)]÷（ 2x ），其中 x=-2，y= .20. 如图所示，在所给正方形网格图中按要求完成下列各题(用直尺画图)：
(1)、画出格点△ABC关于直线DE对称的△A1B1C1；(2)、在DE上画出点Q，使△QBC的周长最小，请简要说明理由。21. 如图所示，O是线段AC、BD的交点，并且AC＝BD，AB＝CD。小明认为证明图中的△AOB和△DOC全等，他说连接BC或AD就可以了，请你用一种方法试一试看：
22. 小明受《乌鸦喝水》故事的启发，利用量筒和体积相同的小球进行了如下操作：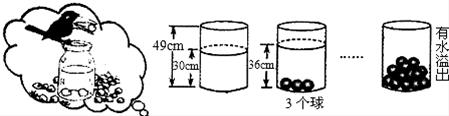
请根据图中给出的信息，解答下列问题：
(1)、放入一个小球量筒中水面升高cm；(2)、求放入小球后量筒中水面的高度y（cm）与小球个数x（个）之间的关系式（不要求写出自变量的取值范围）；(3)、量筒中放入第几个小球时有水溢出？23. 如图，现有一个转盘被平均分成6等份，分别标有数字2、3、4、5、6、7这六个数字，转动转盘，当转盘停止时，指针指向的数字即为转出的数字，求：
(1)、转动转盘，转出的数字大于3的概率是；(2)、现有两张分别写有3和4的卡片，要随机转动转盘，转盘停止后记下转出的数字，与两张卡片上的数字分别作为三条线段的长度。①这三条线段能构成三角形的概率是多少?
②这三条线段能构成等腰三角形的概率是多少?
24. 乘法公式的探究及应用.
(1)、如左图，可以求出阴影部分的面积是（写成两数平方差的形式）；(2)、如右图，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是 ， 长是 ， 面积是（写成多项式乘法的形式）(3)、比较左、右两图的阴影部分面积，可以得到乘法公式（用式子表达）.(4)、运用你所得到的公式，计算下列各题：①
②
25. 如图，在△ABC中，∠ABC为锐角，点D为直线BC上一动点，以AD为直角边且在AD的右侧作等腰直角三角形ADE，∠DAE＝90°，AD＝AE.
(1)、如果AB＝AC，∠BAC＝90°.当点D在线段BC上时，如图1，线段CE、BD的位置关系为 ， 数量关系为
(2)、当点D在线段BC的延长线上时，如图2，（1）中的结论是否仍然成立，请说明理由.(3)、如图3，如果AB≠AC，∠BAC≠90°，点D在线段BC上运动。探究：当∠ACB多少度时，CE⊥BC ？请说明理由.