陕西省渭南市韩城市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-08-05 类型:期末考试
一、选择题:本大题共10个小题,每小题3分,共30分.
-
1. 能使 成立的x的取值范围是( )A、 B、 C、 D、2. 以直角三角形的三边为边向外作正方形,其中两个正方形的面积如图所示,则正方形A的面积为( )
 A、6 B、36 C、64 D、83. 某校5个环保小队参加植树活动,平均每组植树10棵,已知第一、二、三、五组分别植树9棵、12棵、9棵、8棵,则第四小组植树( )A、7棵 B、9棵 C、10棵 D、12棵4. 如图,在平行四边形 中, 于点E,若 ,则 的度数为( )
A、6 B、36 C、64 D、83. 某校5个环保小队参加植树活动,平均每组植树10棵,已知第一、二、三、五组分别植树9棵、12棵、9棵、8棵,则第四小组植树( )A、7棵 B、9棵 C、10棵 D、12棵4. 如图,在平行四边形 中, 于点E,若 ,则 的度数为( )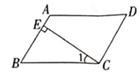 A、28° B、38° C、62° D、72°5. 若点P在一次函数 的图象上,则点P一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 若直线 ( 为常数且 )的图象经过点 ,则关于x的方程 的解为( )A、 B、 C、 D、7. 已知点 , , 都在关于x的一次函数 的图象上,则 , , 之间的大小关系是( )A、 B、 C、 D、8. 在抗击“新型冠状病毒肺炎”疫情中,某社区志愿者小分队年龄如表:
A、28° B、38° C、62° D、72°5. 若点P在一次函数 的图象上,则点P一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 若直线 ( 为常数且 )的图象经过点 ,则关于x的方程 的解为( )A、 B、 C、 D、7. 已知点 , , 都在关于x的一次函数 的图象上,则 , , 之间的大小关系是( )A、 B、 C、 D、8. 在抗击“新型冠状病毒肺炎”疫情中,某社区志愿者小分队年龄如表:年龄(岁)
18
22
30
35
43
人数
2
3
2
2
1
则这10名队员年龄的中位数、众数分别是( )
A、20岁,35岁 B、22岁,22岁 C、26岁、22岁 D、30岁,30岁9. 如图,在矩形 中, 分别是 的中点, ,则 的长为( )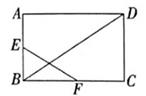 A、6 B、5 C、4 D、310. 如图,正方形 的面积为8,菱形 的面积为4,则 的长是( )
A、6 B、5 C、4 D、310. 如图,正方形 的面积为8,菱形 的面积为4,则 的长是( )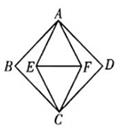 A、4 B、 C、3 D、2
A、4 B、 C、3 D、2二、填空题(本大题共4个小题,每小题3分,共12分)
-
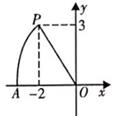
11. 计算 的结果是.12. 如图,点 ,以点O为圆心,以 的长为半径画弧,交x轴的负半轴于点A,则点A的坐标为.
 13. 把直线 向上平移后得到直线 ,若直线 经过点 ,且 ,则直线 的表达式为.14. 如图,在菱形ABCD中,过点A作AH⊥BC,分别交BD,BC于点E,H,F为ED的中点, ,则∠C的度数为
13. 把直线 向上平移后得到直线 ,若直线 经过点 ,且 ,则直线 的表达式为.14. 如图,在菱形ABCD中,过点A作AH⊥BC,分别交BD,BC于点E,H,F为ED的中点, ,则∠C的度数为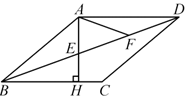
三、解答题:本大题共11个小题,共78分.
-
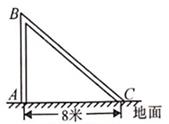
15. 计算:16. 正比例函数 的图象经过点 , ,求a的值.17. 如图,一木杆在离地B处断裂,木杆顶部落在离木杆底部8米处(即 米),已知木杆原长16米,求木杆断裂处B离地面的高度 .
 18. 如图,四边形 是正方形,E是 边上任意一点,连接 ,作 , ,垂足分别为 .求证: .
18. 如图,四边形 是正方形,E是 边上任意一点,连接 ,作 , ,垂足分别为 .求证: .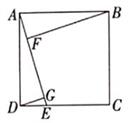 19. 如图,在四边形ABCD中,AB=BC=3,CD= ,DA=5,∠B=90°,求∠BCD的度数
19. 如图,在四边形ABCD中,AB=BC=3,CD= ,DA=5,∠B=90°,求∠BCD的度数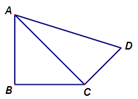 20. 受疫情影响,某地无法按原计划正常开学,在延迟开学期间该地区组织了在线教学活动.开学后,某校针对各班在线教学的个性化落实情况,通过初评决定从甲、乙两个班中推荐一个作为在线教学先进班级,下表是这两个班的五项指标(10分制)的考评得分表(单位:分):
20. 受疫情影响,某地无法按原计划正常开学,在延迟开学期间该地区组织了在线教学活动.开学后,某校针对各班在线教学的个性化落实情况,通过初评决定从甲、乙两个班中推荐一个作为在线教学先进班级,下表是这两个班的五项指标(10分制)的考评得分表(单位:分):班级
课程设置
课程质量
在线答疑
作业情况
学生满意度
甲班
10
10
6
10
7
乙班
10
8
8
9
8
如果学校把“课程设置”、“课程质量”、“在线答疑”、“作业情况”、“学生满意度”这五项指标得分按照2:2:3:1:2的比例确定最终成绩,则应推荐哪个班为在线教学先进班级?
21. 如图,有一张边长为 的正方形纸板,现将该纸板的四个角剪掉,制作一个有底无盖的长方体盒子,剪掉的四个角是面积相等的小正方形,此小正方形的边长为3 .求: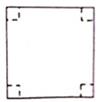 (1)、剪掉四个角后,制作长方体盒子的纸板的面积;(2)、长方体盒子的体积.22. 甲、乙两店销售同一种蔬菜种子.在甲店,不论一次购买数量是多少,价格均为4.5元/ kg .在乙店价格为5元/ kg ,如果一次购买2kg以上的种子,超出2kg部分的种子价格打8折.设小明在同一个店一次购买种子的数量为 xkg . ( ).(1)、设在甲店花费 元,在乙店花费 元,分别求 , 关于x的函数解析式;(2)、若小明计划在同一个店将45元全部用于购买这种蔬菜种子,则他在哪个店购买种子的数量较多?23. 为了选拔一名学生参加全市诗词大赛,学校组织了四次测试,其中甲乙两位同学成绩较为优秀,他们在四次测试中的成绩(单位:分)如表所示:
(1)、剪掉四个角后,制作长方体盒子的纸板的面积;(2)、长方体盒子的体积.22. 甲、乙两店销售同一种蔬菜种子.在甲店,不论一次购买数量是多少,价格均为4.5元/ kg .在乙店价格为5元/ kg ,如果一次购买2kg以上的种子,超出2kg部分的种子价格打8折.设小明在同一个店一次购买种子的数量为 xkg . ( ).(1)、设在甲店花费 元,在乙店花费 元,分别求 , 关于x的函数解析式;(2)、若小明计划在同一个店将45元全部用于购买这种蔬菜种子,则他在哪个店购买种子的数量较多?23. 为了选拔一名学生参加全市诗词大赛,学校组织了四次测试,其中甲乙两位同学成绩较为优秀,他们在四次测试中的成绩(单位:分)如表所示:甲
90
85
95
90
乙
98
82
88
92
通过计算,甲同学在这四次测试中的平均分为90分,分别求出两位同学测试成绩的方差.从成绩稳定性的角度出发,你认为选谁参加比赛较合适?