陕西省西安市莲湖区2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-08-05 类型:期末考试
一、选择题
-
1. 下列四个图标中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. “翻开数学书,恰好翻到第16页”,这个事件是( )A、随机事件 B、必然事件 C、不可能事件 D、确定事件3. 如图所示,△ABC 中 AB 边上的高线是( )
2. “翻开数学书,恰好翻到第16页”,这个事件是( )A、随机事件 B、必然事件 C、不可能事件 D、确定事件3. 如图所示,△ABC 中 AB 边上的高线是( )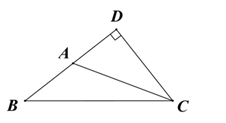 A、线段 DA B、线段 CA C、线段 CD D、线段 BD4. 某人要在规定的时间内加工100个零件,如果用 表示工作效率,用 表示规定的时间,下列说法正确的是( )A、数100和n,t都是常量 B、数100和n都是变量 C、n和t都是变量 D、数100和t都是变量5. 若将一块三角板按如图所示的方式放置, ,则 的度数为( )
A、线段 DA B、线段 CA C、线段 CD D、线段 BD4. 某人要在规定的时间内加工100个零件,如果用 表示工作效率,用 表示规定的时间,下列说法正确的是( )A、数100和n,t都是常量 B、数100和n都是变量 C、n和t都是变量 D、数100和t都是变量5. 若将一块三角板按如图所示的方式放置, ,则 的度数为( )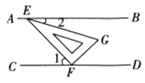 A、20° B、22° C、27° D、34°6. 下列计算正确的是( )A、 B、 C、 D、7. 如果三角形的两边长分别为7和9,那么第三边的长可能是下列数据中的( )A、2 B、13 C、16 D、188. 如图,已知 ,E为 的中点.若 ,则 的长为( )
A、20° B、22° C、27° D、34°6. 下列计算正确的是( )A、 B、 C、 D、7. 如果三角形的两边长分别为7和9,那么第三边的长可能是下列数据中的( )A、2 B、13 C、16 D、188. 如图,已知 ,E为 的中点.若 ,则 的长为( )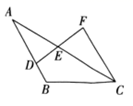 A、 B、 C、 D、9. 如图, 是 的角平分线, ,垂足为 , , , ,则 的面积为( )
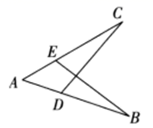
A、 B、 C、 D、9. 如图, 是 的角平分线, ,垂足为 , , , ,则 的面积为( )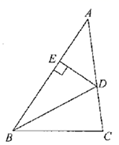 A、4 B、6 C、8 D、1010. 一蓄水池中有 的水,打开排水阀门开始放水后水池中的水量与放水时间有如下关系:
A、4 B、6 C、8 D、1010. 一蓄水池中有 的水,打开排水阀门开始放水后水池中的水量与放水时间有如下关系:放水时间/分
1
2
3
4
…
水池中的水量/
48
46
44
42
…
下列说法不正确的是( )
A、蓄水池每分钟放水 B、放水18分钟后,水池中的水量为 C、放水25分钟后,水池中的水量为 D、放水12分钟后,水池中的水量为二、填空题
-
11. 数据0.0001用科学记数法表示为.12. 如图, ,要使 ,依据 ,应添加的一个条件是.
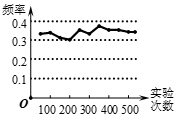
 13. 如图是某小组同学做“频率估计概率”的实验时,绘出的某一实验结果出现的频率折线图,则符合图中这一结果的实验可能是(填序号).
13. 如图是某小组同学做“频率估计概率”的实验时,绘出的某一实验结果出现的频率折线图,则符合图中这一结果的实验可能是(填序号).①抛一枚质地均匀的硬币,落地时结果“正面朝上”;
②在“石头,剪刀,布”的游戏中,小明随机出的是剪刀;
③四张一样的卡片,分别标有数字1,2,3,4,从中随机取出一张,数字是1.
 14. 如图,在 中,点D在 边上, 垂直平分 边,垂足为E,若 ,且 ,则 的度数为.
14. 如图,在 中,点D在 边上, 垂直平分 边,垂足为E,若 ,且 ,则 的度数为.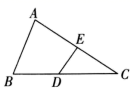
三、解答题
-
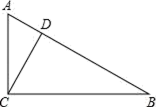
15. 计算:16. 如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B,求证:CD⊥AB.
 17. 先化简,再求值: ,其中 ,18. 如图,已知线段 及锐角 .求作 ,使 .(尺规作图,不写作法,保留作图痕迹)
17. 先化简,再求值: ,其中 ,18. 如图,已知线段 及锐角 .求作 ,使 .(尺规作图,不写作法,保留作图痕迹)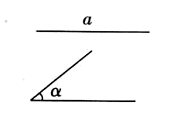 19. 按要求完成下列解题过程,并在括号内填上步骤依据.
19. 按要求完成下列解题过程,并在括号内填上步骤依据.如图,已知 ,求 的度数.
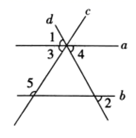
解:因为 ,(_▲__)
,
所以 ,
所以_▲_ _▲_,(_▲_)
所以 _▲_ .(_▲_)
又因为 ,
所以 _▲_°.
20. 如图,在由长度为1个单位长度的小正方形组成的网格中, 的三个顶点A,B,C都在格点上,分别按下列要求在网格中作图:
( 1 )画出与 关于直线l成轴对称的 ;
( 2 )在直线l上找出一点P,使得 的值最大;(保留作图痕迹,并标上字母P)
( 3 )在直线l上找出一点Q,使得 的值最小.(保留作图痕迹,并标上字母Q)
21. 如图:小刚站在河边的A点处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树C处,接着再向前走了30步到达D处,然后他左转 直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他共走了140步.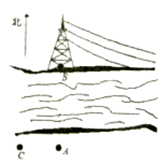 (1)、根据题意,画出示意图;(2)、如果小刚一步大约50厘米,估计小刚在点A处时他与电线塔的距离,并说明理由.22. 小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去参加活动:将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新转动转盘.
(1)、根据题意,画出示意图;(2)、如果小刚一步大约50厘米,估计小刚在点A处时他与电线塔的距离,并说明理由.22. 小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去参加活动:将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新转动转盘. (1)、转盘转到2的倍数的概率是多少?;(2)、你认为这个游戏公平吗?请说明理由.23. 某天,小杰于下午2点骑车从家出发去图书馆,当天按原路返回,如图所示的是在小杰出行的过程中,他离家的距离y(千米)与他离家的时间x(小时)之间的图象.根据图象,完成下列问题:
(1)、转盘转到2的倍数的概率是多少?;(2)、你认为这个游戏公平吗?请说明理由.23. 某天,小杰于下午2点骑车从家出发去图书馆,当天按原路返回,如图所示的是在小杰出行的过程中,他离家的距离y(千米)与他离家的时间x(小时)之间的图象.根据图象,完成下列问题: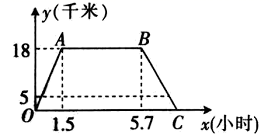 (1)、小杰家距图书馆千米,他骑车去图书馆的速度是千米/时;(2)、已知晚上9点时,小杰距家5千米,请通过计算说明他何时才能回到家.24. 长方形的长为a厘米,宽为b厘米,其中 ,将原长方形的长和宽各增加3厘米,得到的新长方形的面积为 ;将原长方形的长和宽分别减少2厘米,得到的新长方形的面积为 .(1)、若a,b为正整数,请说明 与 的差一定是5的倍数;(2)、若 ,求将原长方形的长和宽分别减少7厘米后得到的新长方形的面积.25. (2020•锦州模拟)问题情境:已知,在等边△ABC中,∠BAC与∠ACB的角平分线交于点O,点M、N分别在直线AC,AB上,且∠MON=60°,猜想CM、MN、AN三者之间的数量关系.
(1)、小杰家距图书馆千米,他骑车去图书馆的速度是千米/时;(2)、已知晚上9点时,小杰距家5千米,请通过计算说明他何时才能回到家.24. 长方形的长为a厘米,宽为b厘米,其中 ,将原长方形的长和宽各增加3厘米,得到的新长方形的面积为 ;将原长方形的长和宽分别减少2厘米,得到的新长方形的面积为 .(1)、若a,b为正整数,请说明 与 的差一定是5的倍数;(2)、若 ,求将原长方形的长和宽分别减少7厘米后得到的新长方形的面积.25. (2020•锦州模拟)问题情境:已知,在等边△ABC中,∠BAC与∠ACB的角平分线交于点O,点M、N分别在直线AC,AB上,且∠MON=60°,猜想CM、MN、AN三者之间的数量关系.方法感悟:小芳的思考过程是在CM上取一点,构造全等三角形,从而解决问题;
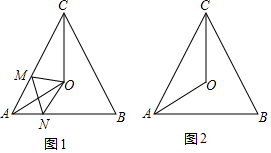
小丽的思考过程是在AB取一点,构造全等三角形,从而解决问题;
(1)、问题解决:如图1,M、N分别在边AC,AB上时,探索CM、MN、AN三者之间的数量关系,并证明;
(2)、如图2,M在边AC上,点N在BA的延长线上时,请你在图2中补全图形,标出相应字母,探索CM、MN、AN三者之间的数量关系,并证明.