陕西省西安市莲湖区2019-2020学年八年级下学期数学期末考试试卷 25

试卷更新日期：2020-08-05 类型：期末考试

进入出卷网下载

一、选择题

1. 若分式 $\frac{x}{x - 2}$ 有意义，则实数x的取值范围是（）

A、 $x > 0$ B、 $x > 2$ C、 $x \neq 0$ D、 $x \neq 2$

查看试题解析
2. 下列由一个正方形和两个相同的等腰直角三角形组成的图形中，为中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若m＜n，则下列结论正确的是（）

A、2m＞2n B、m﹣4＜n﹣4 C、3+m＞3+n D、﹣m＜﹣n

查看试题解析
4. 若n边形的内角和等于外角和的2倍,则边数n为（）

A、 n=4 B、n=5 C、n=6 D、n=7

查看试题解析
5. 课堂上老师在黑板上布置了右框所示的题目，小聪马上发现了其中有一道题目错了，你知道是哪道题目吗？（）
用平方差公式分解下列各式：

（ 1 ） $a^{2} - b^{2}$ （2） $49 x^{2} - y^{2} z^{2}$ （3） $- x^{2} - y^{2}$ （4） $16 m^{2} n^{2} - 25 p^{2}$

A、第1道题 B、第2道题 C、第3道题 D、第4道题

查看试题解析
6. 如图，将 $△ A B C$ 沿直线 $A B$ 向右平移后到达 $△ B D E$ 的位置，连接 $C D$ 、 $C E$ ，若 $△ A C D$ 的面积为10，则四边形 $A C E D$ 的面积为（）

A、15 B、18 C、20 D、24

查看试题解析
7. 如图，若一次函数 $y_{1} = m x + n$ 与 $y_{2} = - x + a$ 的交点坐标为 $(3 ， 2 a - 8)$ ，则 $m x + n < - x + a$ 的解集为（）

A、 $x < 3$ B、 $x < 1$ C、 $x > 3$ D、 $0 < x < 3$

查看试题解析
8. 下列定理中没有逆定理的是（）

A、等腰三角形的两底角相等 B、平行四边形的对角线互相平分 C、角平分线上的点到角两边的距离相等 D、全等三角形的对应角相等

查看试题解析
9. 如图，在四边形 $A B C D$ 中， $A B = C D$ ，对角线 $A C$ 、 $B D$ 相交于点O， $A E ⊥ B D$ 于点E， $C F ⊥ B D$ 于点F，连接 $A F$ 、 $C E$ ，若 $D E = B F$ ，则下列结论不一定正确的是（）

A、 $C F = A E$ B、 $O E = O F$ C、 $△ C D E$ 为直角三角形 D、四边形 $A B C D$ 是平行四边形

查看试题解析
10. 如图，在平行四边形 $A B C D$ 中， $A E ⊥ B C$ 于点E，以点B为中心，取旋转角等于 $∠ A B C$ ，将 $△ B A E$ 顺时针旋转，得到 $△ B A^{'} E^{'}$ .连接 $D A^{'}$ ，若 $∠ A D C = 60 °$ ， $∠ A D A^{'} = 50 °$ ，则 $∠ D A^{'} E^{'}$ 的度数为（）

A、 $130 °$ B、 $140 °$ C、 $150 °$ D、 $160 °$

查看试题解析

二、填空题

11. 多项式 $a x^{2} - a$ 与多项式 $2 x^{2} - 4 x + 2$ 的公因式分别是.

查看试题解析
12. 若关于x的方程 $\frac{2 x - a}{x + 1} = 0$ 的解为负数，则a的取值范围为.

查看试题解析
13. 将一副直角三角板按如图所示的方式放置，其中 $B C = 6 ， E F = 8$ ，把含 $30 °$ 角的三角板向右平移，使顶点B落在含 $45 °$ 角的三角板的斜边 $D F$ 上，则 $G E$ 的长度为.

查看试题解析
14. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $B C = 4 ， A C = 5$ ，点D在边 $B C$ 上，若以 $A D$ 、 $C D$ 为边，以 $A C$ 为对角线，作 $▱ A D C E$ ，则对角线 $D E$ 的最小值为.

查看试题解析

三、解答题

15. 因式分解： $x^{3} y - 9 x y^{3}$ .

查看试题解析
16. 解不等式组 ${\begin{array}{l} 3 (x + 1) > x - 1 ① \\ \frac{x + 9}{2} > 2 x ② \end{array}$ ，并将解集在数轴上表示出来.

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ B A C = 100 °$ ，将 $△ A B C$ 绕点A逆时针旋转 $150 °$ ，得到 $△ A D E$ ，使得点B、C、D恰好在同一条直线上，求 $∠ E$ 的度数.

查看试题解析
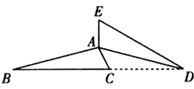18. 如图，在 $△ A B C$ 中， $A B = B C$ ，点D在 $B C$ 的延长线上，连接 $A D$ ，E为 $A D$ 的中点.请用尺规作图法在 $A C$ 边上求作一点F，使得 $E F$ 为 $△ A C D$ 的中位线.（保留作图痕迹，不写作法）

查看试题解析
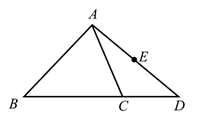19. 先化简再求值： $m - 1 + \frac{2 m - 6}{m^{2} - 9} \div \frac{2 m + 2}{m + 3}$ ，其中m是不等式 $2 (5 m + 3) \geq m - 3 (1 - 2 m)$ 的一个负整数解.

查看试题解析
20. 如图， $△ A B C$ 中任意一点 $P (x_{0} ， y_{0})$ 经平移后对应点为 $P^{'} (x_{0} + 3 ， y_{0} + 4)$ ，将 $△ A B C$ 作同样的平移得到 $△ D E F$ ，其中点A与点D，点B与点E，点C与点F分别对应，请解答下列问题：

(1)、画出 $△ D E F$ ，并写出点D、E、F的坐标..

(2)、若 $△ D E F$ 与 $△ D_{1} E_{1} F_{1}$ 关于原点O成中心对称，直接写出点D的对应点 $D_{1}$ 的坐标.

查看试题解析
21. 如图，在三角形纸片 $A B C$ 中， $∠ B A C$ 的平分线 $A D$ 交 $B C$ 于点D，将 $△ C D E$ 沿 $D E$ 折叠，使点C落在点A处.

(1)、求证： $∠ B A D = ∠ C$ .

(2)、若 $∠ B A D = 33 °$ ，求 $∠ B$ 的度数.

查看试题解析
22. 如图所示的是小聪课后自主学习的一道题，参照小聪的解题思路，回答下列问题：
若 $m^{2} - 2 m n + 2 n^{2} - 8 n + 16 = 0$ ，求m、n的值..

小聪的解答：∵ $m^{2} - 2 m n + 2 n^{2} - 8 n + 16 = 0$ ，

∴ $(m^{2} - 2 m n + n^{2}) + (n^{2} - 8 n + 16) = 0$ ，

∴ ${(m - n)}^{2} + {(n - 4)}^{2} = 0$ ，而 ${(m - n)}^{2} ⩾ 0 ， {(n - 4)}^{2} ⩾ 0$ ，

∴ ${(m - n)}^{2} = 0 ， {(n - 4)}^{2} = 0$ ，

∴ $n = 4 ， m = 4$ .

(1)、 $a^{2} + b^{2} - 4 a + 4 = 0$ ，求a和b的值.

(2)、已知 $△ A B C$ 的三边长a、b、c满足 $a^{2} + 2 b^{2} + c^{2} - 2 a b - 2 b c = 0$ ，关于此三角形的形状有以下命题：①它是等边三角形；②它是等腰三角形；③它是直角三角形.其中是真命题的有.（填序号）

查看试题解析
23. 如图，在平行四边形 $A B C D$ 中，E、F分别为边 $A B$ 、 $C D$ 的中点， $B D$ 是平行四边形 $A B C D$ 的对角线， $A G / / B D$ 交 $C B$ 的延长线于点G.

(1)、求证：四边形 $B E D F$ 是平行四边形.

(2)、若 $A E = D E$ ，求 $∠ G$ 的度数.

查看试题解析
24. 甲、乙两个筑路队共同承担一段一级路的施工任务，甲队单独施工完成此项任务比乙队单独施工完成此项任务多用15天.且甲队单独施工60天和乙队单独施工40天的工作量相同.

(1)、甲、乙两队单独完成此项任务各需多少天？

(2)、若甲、乙两队共同工作了4天后，乙队因设备检修停止施工，由甲队单独继续施工，为了不影响工程进度，甲队的工作效率提高到原来的2倍，要使甲队总的工作量不少于乙队的工作量的2倍，那么甲队至少再单独施工多少天？

查看试题解析
25. 如图

(1)、问题提出：
如图1，在 $△ A B C$ 中， $A B = A C \neq B C$ ，点D和点A在直线 $B C$ 的同侧， $B D = B C$ ， $∠ B A C = 90 °$ ， $∠ D B C = 30 °$ ，连接 $A D$ ，将 $△ A B D$ 绕点A逆时针旋转 $90 °$ 得到 $△ A C D^{'}$ ，连接 $B D^{'}$ （如图2），可求出 $∠ A D B$ 的度数为.

(2)、问题探究：
如图3，在（1）的条件下，若 $∠ B A C = α$ ， $∠ D B C = β$ ，且 $α + β = 120 °$ ， $∠ D B C < ∠ A B C$ ，

①求 $∠ A D B$ 的度数.

②过点A作直线 $A E ⊥ B D$ ，交直线 $B D$ 于点E， $B C = 7 ， A D = 2$ .请求出线段 $B E$ 的长.

查看试题解析