浙江省温州市文成县2020年初中毕业升学考试数学模拟检测试卷
试卷更新日期:2020-08-05 类型:中考模拟
一、选择题(本题有10小题,每小题4分,共40分,每小题只有一个选项是正确的,不选、多选、错选,均不给分)
-
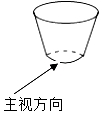
1. 在 , ,0,-2这四个数中,最小的数是( )A、 B、 C、0 D、-22. 如图,桌面上有一个一次性纸杯,它的主视图应是( )
 A、
A、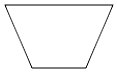 B、
B、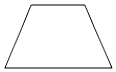 C、
C、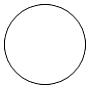 D、
D、 3. 珊溪水库是“温州大水缸”,它占了全市饮用水源的80%,为了遏制水土流失,保护温州500万人民的饮水安全,到2019年底,市政府完成封禁治理任务295000亩,数字295000用科学记数法表示为( )A、2.95×104 B、2.95×105 C、2.95×106 D、0.295×1074. 下列运算正确的是( )A、x3·x²=x5 B、x3+x²=x5 C、(x3)3=x6 D、x6÷x²=x35. 要使分式 有意义,则x的取值应满足( )A、x≠-2 B、x≠1 C、x=-2 D、x>16. 如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC等于( )
3. 珊溪水库是“温州大水缸”,它占了全市饮用水源的80%,为了遏制水土流失,保护温州500万人民的饮水安全,到2019年底,市政府完成封禁治理任务295000亩,数字295000用科学记数法表示为( )A、2.95×104 B、2.95×105 C、2.95×106 D、0.295×1074. 下列运算正确的是( )A、x3·x²=x5 B、x3+x²=x5 C、(x3)3=x6 D、x6÷x²=x35. 要使分式 有意义,则x的取值应满足( )A、x≠-2 B、x≠1 C、x=-2 D、x>16. 如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC等于( ) A、 B、 C、 D、7. 如图,在△ABC中,BD平分∠ABC,E是BC的中点, 过点E作BC的垂线交BD于点F,连结CF。若∠A=50°,∠ACF=40°,则∠CFD的度数为( )
A、 B、 C、 D、7. 如图,在△ABC中,BD平分∠ABC,E是BC的中点, 过点E作BC的垂线交BD于点F,连结CF。若∠A=50°,∠ACF=40°,则∠CFD的度数为( ) A、30° B、45° C、55° D、60°8. 《九章算术》是中国古代的数学专著,第七章“盈不足”专讲盈亏问题,其中记录了这样一道问题:今有人共买物,人出八,盈三;人出七,不足四,问人数,物价几何?条件部分的译文为:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,若设共有x人,物品价格y元,则下面所列方程组正确的是( )A、 B、 C、 D、9. 如图所示,为A,E在反比例函数y= (x>0)的图象上,点B,D在反比例函数y= (k>0) 的图象上,AB∥DE∥y轴,连结DA并延长交y轴于点C,CD∥x轴,△ABC与△ADE的面积之差为 ,则k的值为( )
A、30° B、45° C、55° D、60°8. 《九章算术》是中国古代的数学专著,第七章“盈不足”专讲盈亏问题,其中记录了这样一道问题:今有人共买物,人出八,盈三;人出七,不足四,问人数,物价几何?条件部分的译文为:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,若设共有x人,物品价格y元,则下面所列方程组正确的是( )A、 B、 C、 D、9. 如图所示,为A,E在反比例函数y= (x>0)的图象上,点B,D在反比例函数y= (k>0) 的图象上,AB∥DE∥y轴,连结DA并延长交y轴于点C,CD∥x轴,△ABC与△ADE的面积之差为 ,则k的值为( )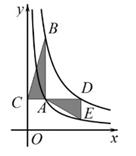 A、4 B、5 C、6 D、810. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2,且AB+AC=8,则BC的长为( )
A、4 B、5 C、6 D、810. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2,且AB+AC=8,则BC的长为( ) A、4 B、6 C、 D、
A、4 B、6 C、 D、二、填空题(本题有6小题,每小题5分,共30分)
-
11. 因式分解:a²-3a=。12. 不等式组 的解集为。13. 一组数据3,2,7,a,5,7的平均数是5,则这组数据的中位数是。14. 如图,四边形ABCD内接于⊙O,⊙O的半径为4cm,∠B=130°,则 的长为cm。
 15. 三个形状大小相同的菱形按如图所示方式摆放,已知∠AOB=∠AOC=90°,菱形的较短对角线长为2cm。若直线AE经过OG的中点P,则△ABC的面积为cm²。
15. 三个形状大小相同的菱形按如图所示方式摆放,已知∠AOB=∠AOC=90°,菱形的较短对角线长为2cm。若直线AE经过OG的中点P,则△ABC的面积为cm²。 16. 文成县珊溪水库素有“温州大水缸”之称,现计划在水库堤坝内侧坡面上建一个水质监测站,监测站平面结构呈等腰三角形(如图△ABC,AB=AC,底边BC所在直线平行于水平线),且一腰(AC)垂直于坡面直线GC(如图所示),中柱AE过底边BC中点D立于坡面直线GC上点E处,AB及其延长线交坡面直线GC于F,AF为一根支撑柱,另外过AE的中点M和点B做一条自动取样传送带,直达坡面直线上点G处(方便取到不同深度的水样,点M、B、G在一条直线上),测得DE=1米,DC=2米,则GF=米(结果保留根号)。
16. 文成县珊溪水库素有“温州大水缸”之称,现计划在水库堤坝内侧坡面上建一个水质监测站,监测站平面结构呈等腰三角形(如图△ABC,AB=AC,底边BC所在直线平行于水平线),且一腰(AC)垂直于坡面直线GC(如图所示),中柱AE过底边BC中点D立于坡面直线GC上点E处,AB及其延长线交坡面直线GC于F,AF为一根支撑柱,另外过AE的中点M和点B做一条自动取样传送带,直达坡面直线上点G处(方便取到不同深度的水样,点M、B、G在一条直线上),测得DE=1米,DC=2米,则GF=米(结果保留根号)。
三、解答题(本题有8小题,共80分,解答需写出必要的文字说明、演算步骤或证明过程)
-
17.(1)、计算:|-4|+ +( -1)0(2)、化简:m(m+2)-(m-1)218. 如图,在菱形ABCD中,点E、F分别在BC,CD上,且CE=CF。
 (1)、求证:△ABE≌△ADF.(2)、若∠BAE=∠EAF=40°,求∠AEB的度数。19. 受疫情影响,小王准备从意大利坐飞机到上海,然后坐班车回文成,意大利到上海仅有A、B两个班次飞机,从上海到文成仅有C、D、E三个班次汽车。(1)、请用列表或树状图的方法,表示小王从意大利到文成的所有可能选择的交通情况;(2)、若同一天有一名新型肺炎感染者乘A班次飞机和D班次汽车从意大利回文成,请你求出小王与这名新型肺炎感染者乘坐班次完全相同的概率。20. 我们把端点都在格点上的线段叫做格点线段。如图在7×7的方格中,现有一格点线段AB及格点C,按要求画图。
(1)、求证:△ABE≌△ADF.(2)、若∠BAE=∠EAF=40°,求∠AEB的度数。19. 受疫情影响,小王准备从意大利坐飞机到上海,然后坐班车回文成,意大利到上海仅有A、B两个班次飞机,从上海到文成仅有C、D、E三个班次汽车。(1)、请用列表或树状图的方法,表示小王从意大利到文成的所有可能选择的交通情况;(2)、若同一天有一名新型肺炎感染者乘A班次飞机和D班次汽车从意大利回文成,请你求出小王与这名新型肺炎感染者乘坐班次完全相同的概率。20. 我们把端点都在格点上的线段叫做格点线段。如图在7×7的方格中,现有一格点线段AB及格点C,按要求画图。 (1)、在图1中画一条格点线段CD,使线段CD和线段AB互相平分;(2)、在图2中画一条格点线段CE,将线段AB分为1:2两部分。21. 如图,在钝角△ABC中,AB=AC,以AC为直径的⊙O交边BA的延长线于点E,交边BC于点D,过点D作⊙O的切线交边AB于点F,交CA的延长线于点G。
(1)、在图1中画一条格点线段CD,使线段CD和线段AB互相平分;(2)、在图2中画一条格点线段CE,将线段AB分为1:2两部分。21. 如图,在钝角△ABC中,AB=AC,以AC为直径的⊙O交边BA的延长线于点E,交边BC于点D,过点D作⊙O的切线交边AB于点F,交CA的延长线于点G。 (1)、求证:点F是线段EB的中点。(2)、若sin∠G= ,CG=4。求AE的长。22. 如图,在平面直角坐标系中,二次函数y= x²- x-2的图象交x轴于点A,B(点A在点B的左侧),与y轴交于点C,函数图象的顶点为点D。
(1)、求证:点F是线段EB的中点。(2)、若sin∠G= ,CG=4。求AE的长。22. 如图,在平面直角坐标系中,二次函数y= x²- x-2的图象交x轴于点A,B(点A在点B的左侧),与y轴交于点C,函数图象的顶点为点D。 (1)、求点B,D的坐标,并根据该函数图象写出当x>0时y的取值范围;(2)、将点C向上平移m(m>0)个单位到点G,过点G作x轴的平行线,与二次函数的图象交于点E,F,若FG=2EG,求m的值。23. 某校计划对100名优秀作品学生设立一、二、三等奖分别奖励一套数学用具、一本笔记本、一支水笔。已知购买1套数学用具和2本笔记本共35元,购买2套数学用具和3本笔记本共60元,一支水笔的单价为2元。设获一、二、三等奖的人数分别为a人,b人,c人,且a<b<c。(1)、求数学用具和笔记本的单价;(2)、因购买数量较多,商家给予优惠:每购买1套数学用具和1本笔记本赠送2支水笔。
(1)、求点B,D的坐标,并根据该函数图象写出当x>0时y的取值范围;(2)、将点C向上平移m(m>0)个单位到点G,过点G作x轴的平行线,与二次函数的图象交于点E,F,若FG=2EG,求m的值。23. 某校计划对100名优秀作品学生设立一、二、三等奖分别奖励一套数学用具、一本笔记本、一支水笔。已知购买1套数学用具和2本笔记本共35元,购买2套数学用具和3本笔记本共60元,一支水笔的单价为2元。设获一、二、三等奖的人数分别为a人,b人,c人,且a<b<c。(1)、求数学用具和笔记本的单价;(2)、因购买数量较多,商家给予优惠:每购买1套数学用具和1本笔记本赠送2支水笔。①若赠送的水笔恰好奖励给三等奖的学生,求购买奖品的最小金额。
②若二等奖人数是一等奖人数的1.5倍,且一等奖人数超过20人,已知在购买奖品时仍需要购买水笔,求购买奖品的金额。
24. 如图,在Rt△ABC中,∠ABC=90°,E为AB边上一点,过E、B、C三点的圆交线段AC于点D,点A关于直线BD的对称点F落在⊙O上,连CF。 (1)、求证:∠BCA=45°;(2)、若AB=6,点E在运动过程中,当点F关于直线CD的对称点正好落在△BDF的边上时,求CD的长;(3)、当tan∠CDF= 时,设△CDF的面积为S1 , △BDE的面积为S2 , 求 的值。
(1)、求证:∠BCA=45°;(2)、若AB=6,点E在运动过程中,当点F关于直线CD的对称点正好落在△BDF的边上时,求CD的长;(3)、当tan∠CDF= 时,设△CDF的面积为S1 , △BDE的面积为S2 , 求 的值。