江苏省常州市2020年中考数学试卷
试卷更新日期:2020-08-04 类型:中考真卷
一、选择题
-
1. 2的相反数是( )A、 B、 C、2 D、-22. 计算 的结果是( )A、 B、 C、 D、3. 如图是某几何体的三视图,该几何体是( )
 A、圆柱 B、三棱柱 C、四棱柱 D、四棱锥4. 8的立方根是( )A、2 B、±2 C、±2 D、25. 如果 ,那么下列不等式正确的是( )A、 B、 C、 D、6. 如图,直线a、b被直线c所截, , ,则 的度数是( )
A、圆柱 B、三棱柱 C、四棱柱 D、四棱锥4. 8的立方根是( )A、2 B、±2 C、±2 D、25. 如果 ,那么下列不等式正确的是( )A、 B、 C、 D、6. 如图,直线a、b被直线c所截, , ,则 的度数是( ) A、30° B、40° C、50° D、60°7. 如图, 是 的弦,点C是优弧 上的动点(C不与A、B重合), ,垂足为H,点M是 的中点.若 的半径是3,则 长的最大值是( )
A、30° B、40° C、50° D、60°7. 如图, 是 的弦,点C是优弧 上的动点(C不与A、B重合), ,垂足为H,点M是 的中点.若 的半径是3,则 长的最大值是( )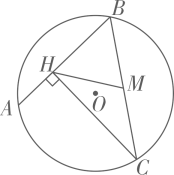 A、3 B、4 C、5 D、68. 如图,点D是 内一点, 与x轴平行, 与y轴平行, .若反比例函数 的图像经过A、D两点,则k的值是( )
A、3 B、4 C、5 D、68. 如图,点D是 内一点, 与x轴平行, 与y轴平行, .若反比例函数 的图像经过A、D两点,则k的值是( )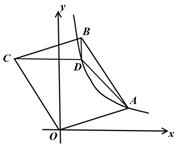 A、 B、4 C、 D、6
A、 B、4 C、 D、6二、填空题
-
9. 计算:|-2|+(π-1)0=.10. 若代数式 有意义,则实数x的取值范围是.11. 地球半径大约是 ,将6400用科学记数法表示为.12. 分解因式:x3-x= .13. 若一次函数 y=kx+2 的函数值y随自变量x增大而增大,则实数k的取值范围是.14. 若关于x的方程 有一个根是1,则 .15. 如图,在 中, 的垂直平分线分别交 、 于点E、F.若 是等边三角形,则 °.
 16. 数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形 中, .如图,建立平面直角坐标系 ,使得边 在x轴正半轴上,点D在y轴正半轴上,则点C的坐标是.
16. 数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形 中, .如图,建立平面直角坐标系 ,使得边 在x轴正半轴上,点D在y轴正半轴上,则点C的坐标是.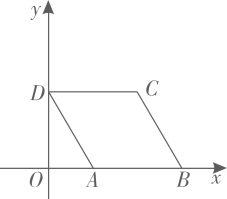 17. 如图,点C在线段 上,且 ,分别以 、 为边在线段 的同侧作正方形 、 ,连接 、 ,则 .
17. 如图,点C在线段 上,且 ,分别以 、 为边在线段 的同侧作正方形 、 ,连接 、 ,则 . 18. 如图,在 中, ,D、E分别是 、 的中点,连接 ,在直线 和直线 上分别取点F、G,连接 、 .若 ,且直线 与直线 互相垂直,则 的长为.
18. 如图,在 中, ,D、E分别是 、 的中点,连接 ,在直线 和直线 上分别取点F、G,连接 、 .若 ,且直线 与直线 互相垂直,则 的长为.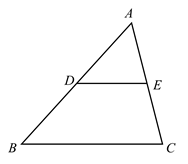
三、解答题
-
19. 先化简,再求值: ,其中 .20. 解方程和不等式组:(1)、 ;(2)、21. 为了解某校学生对球类运动的喜爱情况,调查小组就打排球、打乒乓球、打篮球、踢足球四项球类运动对该校学生进行了“你最喜爱的球类运动”的抽样调查,并根据调查结果绘制成如下统计图.

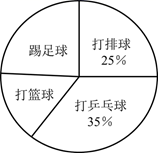 (1)、本次抽样调查的样本容量是;(2)、补全条形统计图;(3)、该校共有2000名学生,请你估计该校最喜爱“打篮球”的学生人数.22. 在3张相同的小纸条上分别标上1、2、3这3个号码,做成3支签,放在一个不透明的盒子中.(1)、搅匀后从中随机抽出1支签,抽到1号签的概率是;(2)、搅匀后先从中随机抽出1支签(不放回),再从余下的2支签中随机抽出1支签,求抽到的2支签上签号的和为奇数的概率.23. 已知:如图,点A、B、C、D在一条直线上, .
(1)、本次抽样调查的样本容量是;(2)、补全条形统计图;(3)、该校共有2000名学生,请你估计该校最喜爱“打篮球”的学生人数.22. 在3张相同的小纸条上分别标上1、2、3这3个号码,做成3支签,放在一个不透明的盒子中.(1)、搅匀后从中随机抽出1支签,抽到1号签的概率是;(2)、搅匀后先从中随机抽出1支签(不放回),再从余下的2支签中随机抽出1支签,求抽到的2支签上签号的和为奇数的概率.23. 已知:如图,点A、B、C、D在一条直线上, .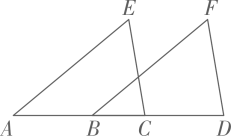 (1)、求证: ;(2)、若 ,求 的度数.24. 某水果店销售苹果和梨,购买1千克苹果和3千克梨共需26元,购买2千克苹果和1千克梨共需22元.(1)、求每千克苹果和每千克梨的售价;(2)、如果购买苹果和梨共15千克,且总价不超过100元,那么最多购买多少千克苹果?25. 如图,正比例函数 的图像与反比例函数 的图像交于点 .点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图象于点C,交正比例函数的图象于点D.
(1)、求证: ;(2)、若 ,求 的度数.24. 某水果店销售苹果和梨,购买1千克苹果和3千克梨共需26元,购买2千克苹果和1千克梨共需22元.(1)、求每千克苹果和每千克梨的售价;(2)、如果购买苹果和梨共15千克,且总价不超过100元,那么最多购买多少千克苹果?25. 如图,正比例函数 的图像与反比例函数 的图像交于点 .点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图象于点C,交正比例函数的图象于点D.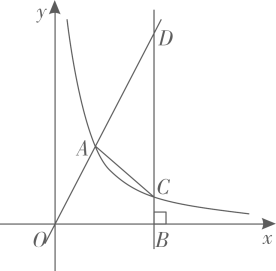 (1)、求a的值及正比例函数 的表达式;(2)、若 ,求 的面积.26. 如图1,点B在线段 上,Rt△ ≌Rt△ , , , .
(1)、求a的值及正比例函数 的表达式;(2)、若 ,求 的面积.26. 如图1,点B在线段 上,Rt△ ≌Rt△ , , , .
 (1)、点F到直线 的距离是;(2)、固定△ ,将△ 绕点C按顺时针方向旋转30°,使得 与 重合,并停止旋转.
(1)、点F到直线 的距离是;(2)、固定△ ,将△ 绕点C按顺时针方向旋转30°,使得 与 重合,并停止旋转.①请你在图1中用直尺和圆规画出线段 经旋转运动所形成的平面图形(用阴影表示,保留画图痕迹,不要求写画法)该图形的面积为;
②如图2,在旋转过程中,线段 与 交于点O,当 时,求 的长.
27. 如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点”,把 的值称为⊙I关于直线a的“特征数”.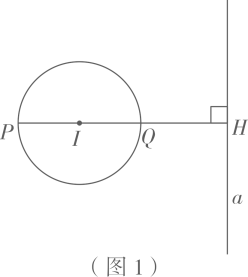
 (1)、如图2,在平面直角坐标系 中,点E的坐标为 ,半径为1的⊙O与两坐标轴交于点A、B、C、D.
(1)、如图2,在平面直角坐标系 中,点E的坐标为 ,半径为1的⊙O与两坐标轴交于点A、B、C、D.①过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点_▲__(填“A”、“B”、“C”或“D”),⊙O关于直线m的“特征数”为_▲__;
②若直线n的函数表达式为 ,求 关于直线n的“特征数”;
(2)、在平面直角坐标系 中,直线l经过点 ,点F是坐标平面内一点,以F为圆心, 为半径作⊙F.若⊙F与直线l相离,点 是⊙F关于直线l的“远点”,且⊙F关于直线l的“特征数”是 ,求直线l的函数表达式.28. 如图,二次函数 的图像与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,抛物线过点 ,且顶点为D,连接 、 、 、 .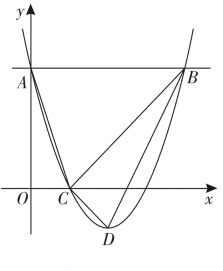
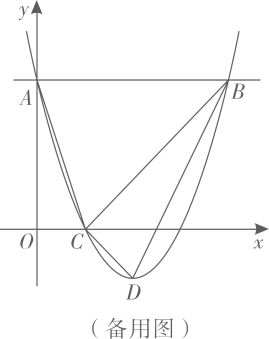 (1)、填空: ;(2)、点P是抛物线上一点,点P的横坐标大于1,直线 交直线 于点Q.若 ,求点P的坐标;(3)、点E在直线 上,点E关于直线 对称的点为F,点F关于直线 对称的点为G,连接 .当点F在x轴上时,直接写出 的长.
(1)、填空: ;(2)、点P是抛物线上一点,点P的横坐标大于1,直线 交直线 于点Q.若 ,求点P的坐标;(3)、点E在直线 上,点E关于直线 对称的点为F,点F关于直线 对称的点为G,连接 .当点F在x轴上时,直接写出 的长.