湖北省武汉市2020年中考数学试卷
试卷更新日期:2020-08-04 类型:中考真卷
一、选择题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 式子 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、3. 两个不透明的口袋中各有三个相同的小球,将每个口袋中的小球分别标号为1,2,3.从这两个口袋中分别摸出一个小球,则下列事件为随机事件的是( )A、两个小球的标号之和等于1 B、两个小球的标号之和等于6 C、两个小球的标号之和大于1 D、两个小球的标号之和大于64. 现实世界中,对称现象无处不在,中国的方块字中有些也只有对称性,下列汉字是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、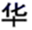 5. 下图是由4个相同的正方体组成的立体图形,它的左视图是( )
5. 下图是由4个相同的正方体组成的立体图形,它的左视图是( )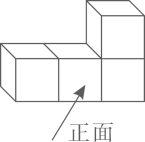 A、
A、 B、
B、 C、
C、 D、
D、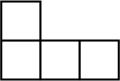 6. 某班从甲、乙、丙、丁四位选中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是( )A、 B、 C、 D、7. 若点 , 在反比例函数 的图象上,且 ,则a的取值范围是( )A、 B、 C、 D、 或8. 一个容器有进水管和出水管,每分钟的进水和出水是两个常数.从某时刻开始 内只进水不出水,从第 到第 内既进水又出水,从第 开始只出水不进水,容器内水量y(单位:L)与时间x(单位: )之间的关系如图所示,则图中a的值是( )
6. 某班从甲、乙、丙、丁四位选中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是( )A、 B、 C、 D、7. 若点 , 在反比例函数 的图象上,且 ,则a的取值范围是( )A、 B、 C、 D、 或8. 一个容器有进水管和出水管,每分钟的进水和出水是两个常数.从某时刻开始 内只进水不出水,从第 到第 内既进水又出水,从第 开始只出水不进水,容器内水量y(单位:L)与时间x(单位: )之间的关系如图所示,则图中a的值是( ) A、32 B、34 C、36 D、389. 如图,在半径为3的⊙O中, 是直径, 是弦,D是 的中点, 与 交于点E.若E是 的中点,则 的长是( )
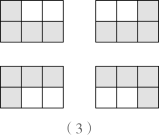
A、32 B、34 C、36 D、389. 如图,在半径为3的⊙O中, 是直径, 是弦,D是 的中点, 与 交于点E.若E是 的中点,则 的长是( )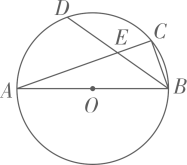 A、 B、 C、 D、10. 下列图中所有小正方形都是全等的.图(1)是一张由4个小正方形组成的“L”形纸片,图(2)是一张由6个小正方形组成的 方格纸片.把“L”形纸片放置在图(2)中,使它恰好盖住其中的4个小正方形,共有如图(3)中的4种不同放置方法,图(4)是一张由36个小正方形组成的 方格纸片,将“L”形纸片放置在图(4)中,使它恰好盖住其中的4个小正方形,共有 种不同放置方法,则 的值是( )
A、 B、 C、 D、10. 下列图中所有小正方形都是全等的.图(1)是一张由4个小正方形组成的“L”形纸片,图(2)是一张由6个小正方形组成的 方格纸片.把“L”形纸片放置在图(2)中,使它恰好盖住其中的4个小正方形,共有如图(3)中的4种不同放置方法,图(4)是一张由36个小正方形组成的 方格纸片,将“L”形纸片放置在图(4)中,使它恰好盖住其中的4个小正方形,共有 种不同放置方法,则 的值是( )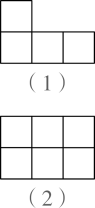
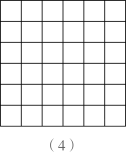 A、160 B、128 C、80 D、48
A、160 B、128 C、80 D、48二、填空题
-
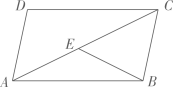
11. 计算 的结果是.12. 热爱劳动,劳动最美!某合作学习小组6名同学一周居家劳动的时间(单位:h),分别为:4,3,3,5,5,6.这组数据的中位数是.13. 计算 的结果是.14. 在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图, 是平行四边形 的对角线,点 在 上, , ,则 的大小是.
 15. 抛物线 ( , , 为常数, )经过 , 两点,下列四个结论:
15. 抛物线 ( , , 为常数, )经过 , 两点,下列四个结论:①一元二次方程 的根为 , ;
②若点 , 在该抛物线上,则 ;
③对于任意实数 ,总有 ;
④对于 的每一个确定值,若一元二次方程 ( 为常数, )的根为整数,则 的值只有两个.
其中正确的结论是(填写序号).
16. 如图,折叠矩形纸片 ,使点D落在 边的点M处, 为折痕, , .设 的长为t,用含有t的式子表示四边形 的面积是.
三、解答题
-
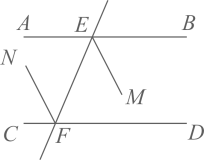
17. 计算: .18. 如图,直线 分别与直线 , 交于点E,F. 平分 , 平分 ,且 ∥ .求证: ∥ .
 19. 为改善民生;提高城市活力,某市有序推行“地摊经济”政策.某社区志愿者随机抽取该社区部分居民,按四个类别:A表示“非常支持”,B表示“支持”,C表示“不关心”,D表示“不支持”,调查他们对该政策态度的情况,将结果绘制成如下两幅不完整的统计图.根据图中提供的信息,解决下列问题:
19. 为改善民生;提高城市活力,某市有序推行“地摊经济”政策.某社区志愿者随机抽取该社区部分居民,按四个类别:A表示“非常支持”,B表示“支持”,C表示“不关心”,D表示“不支持”,调查他们对该政策态度的情况,将结果绘制成如下两幅不完整的统计图.根据图中提供的信息,解决下列问题:
 (1)、这次共抽取了名居民进行调查统计,扇形统计图中, 类所对应的扇形圆心角的大小是;(2)、将条形统计图补充完整;(3)、该社区共有2000名居民,估计该社区表示“支持”的B类居民大约有多少人?20. 在 的网格中建立如图的平面直角坐标系,四边形 的顶点坐标分别为 , , , .仅用无刻度的直尺在给定网格中按下列步骤完成画图,并回答问题:
(1)、这次共抽取了名居民进行调查统计,扇形统计图中, 类所对应的扇形圆心角的大小是;(2)、将条形统计图补充完整;(3)、该社区共有2000名居民,估计该社区表示“支持”的B类居民大约有多少人?20. 在 的网格中建立如图的平面直角坐标系,四边形 的顶点坐标分别为 , , , .仅用无刻度的直尺在给定网格中按下列步骤完成画图,并回答问题: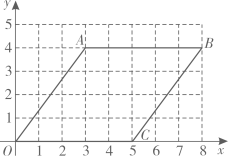 (1)、将线段 绕点C逆时针旋转 ,画出对应线段 ;(2)、在线段 上画点E,使 (保留画图过程的痕迹);(3)、连接 ,画点E关于直线 的对称点F,并简要说明画法.21. 如图,在 中, ,以 为直径的⊙O交 于点D, 与过点D的切线互相垂直,垂足为E.
(1)、将线段 绕点C逆时针旋转 ,画出对应线段 ;(2)、在线段 上画点E,使 (保留画图过程的痕迹);(3)、连接 ,画点E关于直线 的对称点F,并简要说明画法.21. 如图,在 中, ,以 为直径的⊙O交 于点D, 与过点D的切线互相垂直,垂足为E. (1)、求证: 平分 ;(2)、若 ,求 的值.22. 某公司分别在A,B两城生产同种产品,共100件.A城生产品的总成本y(万元)与产品数量x(件)之间具有函数关系 ,当 时, ;当 时, .B城生产产品的每件成本为70万元.(1)、求a,b的值;(2)、当A,B两城生产这批产品的总成本的和最少时,求A,B两城各生产多少件?(3)、从A城把该产品运往C,D两地的费用分别为m万元/件和3万元/件;从 城把该产品运往C,D两地的费用分别为1万元/件和2万元/件,C地需要90件,D地需要10件,在(2)的条件下,直接写出A,B两城总运费的和的最小值(用含有m的式子表示).23. 如图
(1)、求证: 平分 ;(2)、若 ,求 的值.22. 某公司分别在A,B两城生产同种产品,共100件.A城生产品的总成本y(万元)与产品数量x(件)之间具有函数关系 ,当 时, ;当 时, .B城生产产品的每件成本为70万元.(1)、求a,b的值;(2)、当A,B两城生产这批产品的总成本的和最少时,求A,B两城各生产多少件?(3)、从A城把该产品运往C,D两地的费用分别为m万元/件和3万元/件;从 城把该产品运往C,D两地的费用分别为1万元/件和2万元/件,C地需要90件,D地需要10件,在(2)的条件下,直接写出A,B两城总运费的和的最小值(用含有m的式子表示).23. 如图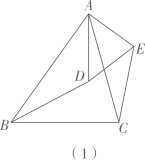
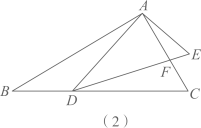
 (1)、问题背景:如图(1),已知 ,求证: ;(2)、尝试应用:如图(2),在 和 中, , , 与 相交于点 .点 在 边上, ,求 的值;(3)、拓展创新:如图(3),D是 内一点, , , , ,直接写出 的长.24. 将抛物线 向下平移6个单位长度得到抛物线 ,再将抛物线 向左平移2个单位长度得到抛物线 .
(1)、问题背景:如图(1),已知 ,求证: ;(2)、尝试应用:如图(2),在 和 中, , , 与 相交于点 .点 在 边上, ,求 的值;(3)、拓展创新:如图(3),D是 内一点, , , , ,直接写出 的长.24. 将抛物线 向下平移6个单位长度得到抛物线 ,再将抛物线 向左平移2个单位长度得到抛物线 .
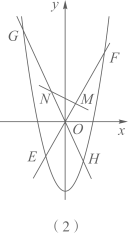 (1)、直接写出抛物线 , 的解析式;(2)、如图(1),点 在抛物线 对称轴 右侧上,点 在对称轴 上, 是以 为斜边的等腰直角三角形,求点 的坐标;(3)、如图(2),直线 ( , 为常数)与抛物线 交于 , 两点, 为线段 的中点;直线 与抛物线 交于 , 两点, 为线段 的中点.求证:直线 经过一个定点.
(1)、直接写出抛物线 , 的解析式;(2)、如图(1),点 在抛物线 对称轴 右侧上,点 在对称轴 上, 是以 为斜边的等腰直角三角形,求点 的坐标;(3)、如图(2),直线 ( , 为常数)与抛物线 交于 , 两点, 为线段 的中点;直线 与抛物线 交于 , 两点, 为线段 的中点.求证:直线 经过一个定点.